
FWF Stand-alone project P 25975-N25, 2013-2016
Strange Attractors and Inverse Limit Spaces
Short desciption
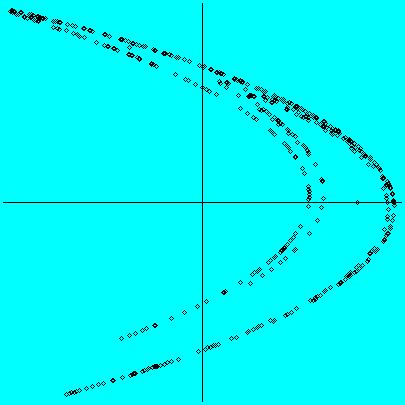
This proposal concerns the topological structure of strange attractors of Hénon type, which emerge universally in chaotic dynamics, for example, in
generic unfoldings of homoclinic bifurcations.
The standard example are the Hénon attractors themselves, but in its
most transparent, linearised form, they are produced by the Lozi map.
Despite its widespread appearance in chaotic dynamics, the topological structure
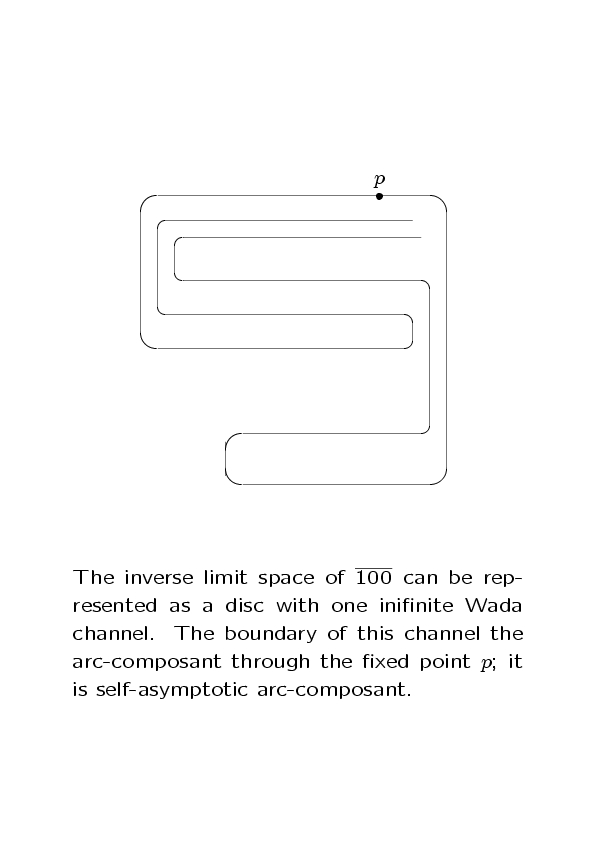
of Hénon-like attractors is poorly understood. This proposal suggest to use techniques from unimodal inverse limit spaces (UILs), and specifically
the classification methods that led to the solution of the Ingram conjecture,
to explore the substructures and possible classification of
Hénon-like attractors.
This will be combined with symbolic and graphic techniques to
display Hénon-attractors and their substructure on small scale.
Workshop
Project funds were used to fund the Workshop
"Dynamical systems and continuum theory",
June 29-July 3 2015, at the
University of Vienna,
organized by Jan Boroński, Henk Bruin and Sonja Štimac.
Apart from 8 invited talks, there were three minicourses.
Click for
the program
PhD defense Jernej Činč on December 14.
Reading committee: Jan Boronski, Chris Good, Peter Raith.
Publications completed or initiated in this project
- Henk Bruin and Sonja Štimac
Fibonacci-like unimodal inverse limit spaces
and the core Ingram conjecture,
Preprint 2013 and revised 2014 [.pdf].
Topological Methods in Nonlinear Analysis (TMNA)
47 (2016), 147--185. DOI: 10.12775/TMNA.2016.001
Arxiv: 1305.4621
- Ana Anušić, Henk Bruin and Jernej Činč
The Core Ingram Conjecture for non-recurrent critical points
Preprint 2015, revision 2016 [.pdf]
Arxiv:1512.07073
to appear in Fundamenta Mathematica.
- Jozef Bobok and Henk Bruin
Constant slope maps and the Vere-Jones classification.
Preprint 2016 [.pdf].
Entropy 18(6), 234, 2016. DOI:10.3390/e18060234
Arxiv: 1602.06905
- Ana Anušić, Henk Bruin and Jernej Činč
Uncountably many planar embeddings of unimodal inverse limit spaces
Preprint 2016 [.pdf]
Arxiv: 1603.03887
Discrete Cont. Dyn. Sys. 37 (2017) no. 5. 2285-2300.
- Ana Anušić and Jernej Činč
Accessible points of planar embeddings of unimodal inverse limit spaces
Arxiv: 1710.11519.
- Ana Anušić, Henk Bruin and Jernej Činč
Intrinsically inaccessible points of chainable continua
In preparation


