Victor J. W. Guo and Christian Krattenthaler

Some divisibility properties of binomial and q-binomial coefficients

(16 pages)

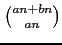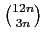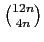Abstract. We first prove that if a has a prime factor not dividing b then there are infinitely many positive integers n such that $ \binom {an+bn} { an}$ is not divisible by bn+1. This confirms a recent conjecture of Z.-W. Sun. 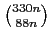Moreover, we provide some new divisibility properties of binomial coefficients: for example, we prove that $ \binom {12n} { 3n}$ and $ \binom {12n} { 4n}$ are divisible by 6n-1, and that $ \binom {330n} { 88n}$ is divisible by 66n-1, for all positive integers n. As we show, the latter results are in fact consequences of divisibility and positivity results for quotients of q-binomial coefficients by q-integers, generalising the positivity of q-Catalan numbers. We also put forward several related conjectures.

The following versions are available:

Back to Christian Krattenthaler's home page.