Nächste Seite: 1.2 Metriken Aufwärts: 1 Konvergenz von Folgen Vorherige Seite: 1 Konvergenz von Folgen Inhalt Index
Wir wollen damit beginnen anhand einiger weniger Bespiele zu erläutern, worum wir uns mit Analysis und damit mit Grenzprozessen oder ungenau formuliert dem unendlich Kleinen beschäftigen müssen.
1.1.1 Der freie Fall.
In der Physik erkennt man, daß sich Körper, die keinen Kräften ausgesetzt sind,
gleichförmig bewegen, d.h. ihre Geschwindigkeit konstant bleibt, also in gleicher Zeit
gleich langer Weg zurückgelegt wird.
Falls andererseits eine konstante Kraft ![]() (wie z.B. die Erdanziehung in Bodennähe)
auf den Körper wirkt,
so ändert sich seine Geschwindigkeit proportional zur vergangenen Zeit und zur Kraft.
Sei also
(wie z.B. die Erdanziehung in Bodennähe)
auf den Körper wirkt,
so ändert sich seine Geschwindigkeit proportional zur vergangenen Zeit und zur Kraft.
Sei also ![]() die Geschwindigkeit zum Zeitpunkt
die Geschwindigkeit zum Zeitpunkt ![]() (wir setzen der Einfachheit
halber
(wir setzen der Einfachheit
halber ![]() voraus) und
voraus) und ![]() eine Zeitspanne,
dann gilt
eine Zeitspanne,
dann gilt
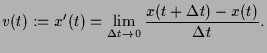
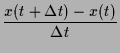 |
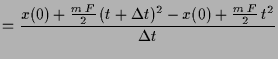 |
|
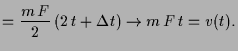 |
1.1.2 Berechnung von ![]() .
.
Per Definition ist ![]() die Länge eines Halbkreises mit Radius 1
oder auch die Fläche eines Vollkreises mit selben Radius.
Natürlich ist nicht klar, daß dies die gleiche Zahl liefert.
Auch ist uns vorerst nur bekannt, wie die Fläche von Rechtecken und damit von
rechtwinkeligen Dreiecken berechnet werden kann. Und ebenso nur die Länge
von Polygonzügen. Die Länge einer Kurve
die Länge eines Halbkreises mit Radius 1
oder auch die Fläche eines Vollkreises mit selben Radius.
Natürlich ist nicht klar, daß dies die gleiche Zahl liefert.
Auch ist uns vorerst nur bekannt, wie die Fläche von Rechtecken und damit von
rechtwinkeligen Dreiecken berechnet werden kann. Und ebenso nur die Länge
von Polygonzügen. Die Länge einer Kurve
![]() können wir nur durch
die Länge von Polygonzügen
können wir nur durch
die Länge von Polygonzügen
![]() annähern, wobei
annähern, wobei
![]() eine Zerlegung der Strecke von 0 nach
eine Zerlegung der Strecke von 0 nach ![]() ist.
Wir definieren folglich die Länge der Kurve
ist.
Wir definieren folglich die Länge der Kurve
![]() als
als
![]() .
Nun betrachten wir regelmäßige Vielecke, die wir dem Einheitskreis ein- und umschreiben.
Die Fläche des Einheitskreises liegt dann offensichtlich zwischen jener
der eingeschriebenen und der umgeschriebenen Vielecke.
.
Nun betrachten wir regelmäßige Vielecke, die wir dem Einheitskreis ein- und umschreiben.
Die Fläche des Einheitskreises liegt dann offensichtlich zwischen jener
der eingeschriebenen und der umgeschriebenen Vielecke.
![\includegraphics[]{pic-002BW}](img142.png)
Es sei
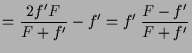 |
||
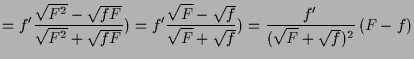 |
||
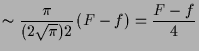 |
![\includegraphics[]{pic-005}](img143.png)
Wir werden später die Fläche des Einheitskreises wie folgt durch ein Integral berechnen
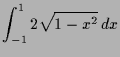 |
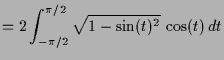 |
|
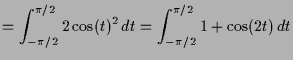 |
||
![$\displaystyle = \left[t+\frac{\sin(2t)}2\right]_{-\pi/2}^{\pi/2} = \pi + \frac{\sin(\pi)}2-\frac{\sin(-\pi)}2 = \pi$](img81.png) |
1.1.3 Rekursive Berechnung von ![]() .
.
Die Wurzel erfüllt
![]() , d.h. wir versuchen
, d.h. wir versuchen ![]() in ein Produkt
in ein Produkt
![]() zweier gleicher Zahlen zu zerlegen.
Sei o.B.d.A.
zweier gleicher Zahlen zu zerlegen.
Sei o.B.d.A. ![]() , andernfalls bestimmen wir
, andernfalls bestimmen wir
![]() .
Wir versuchen es mit
.
Wir versuchen es mit ![]() , dann wäre
, dann wäre ![]() und somit
und somit
![]() . Also probieren wir ein neues besseres
. Also probieren wir ein neues besseres
![]() .
Das zugehörige
.
Das zugehörige ![]() erfüllt
erfüllt
![]() , denn
, denn
![]() . Fahren wir so fort, so erhalten wir
Folgen
. Fahren wir so fort, so erhalten wir
Folgen
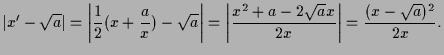
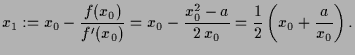
![\includegraphics[]{pic-015}](img144.png)
1.1.4 Brennspiegel.
Wir wollen nun einen Spiegel konstruieren, der parallel einfallende Lichtstrahlen
in einem Punkt konzentriert. Das ist natürlich auch für Radioteleskope und
in umgekehrter Richtung für Scheinwerfer interessant.
Da Lichtstrahlen kürzeste Verbindungslinien sind, ist der Einfallswinkel auf eine
Fläche gleich dem Ausfallswinkel.
Sei also ![]() ein Punkt auf der Schnittkurve und der Anstieg der Schnittkurve
ein Punkt auf der Schnittkurve und der Anstieg der Schnittkurve
![]() .
.
![\includegraphics[]{pic-001}](img145.png)
Die Ähnlichkeit von Dreiecken ergibt
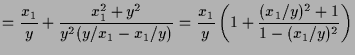 |
||
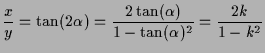
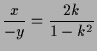
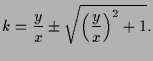
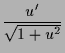 |
||
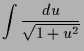 |
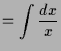 |
|
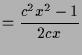 |
||
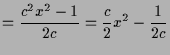 |
Andreas Kriegl 2001-07-01