Walter Schachermayer

On Vershik's Standardness Criterion and Tsirelson's Notion of Cosiness.

M. Emery, W. Schachermayer
Séminaire de Probabilités XXXV, Springer Lecture Notes in Mathematics, Vol. 1755 (2001), pp. 265-305. 

Abstract:

Building on work done by A. Vershik some thirty years ago, the insight into different types of filtrations has recently seen important progress, due in particular to B. Tsirelson, and L. Dubins, J. Feldman, M. Smorodinsky, B. Tsirelson. Key concepts are the notions of standard filtrations (due to A. Vershik) and cosy filtrations (due to B. Tsirelson). We investigate the relation between these two concepts and try to provide a comprehensive and self­contained presentation of the topic.

Part of this work is expository, and consists in translating into a probabilist's language Vershik's necessary and sufficient condition for standardness, and his theorem on lacunary isomorphism. There are also original results: Theorem 2 proves that standardness is in fact equivalent to a certain variant of the notion of cosiness, which we call I­cosiness; an example borrowed from Vershik and Smorodinsky then shows that I­cosiness is strictly stronger than another variant, D­cosiness, used in earlier works. Another new result is a (negative) answer to a question of H. von Weizsaecker: the last section gives an example of a filtration (F_n)_{n \in -N} and a \sigma­field B such that F_0 and B are 'almost independent', but nevertheless

Preprints:

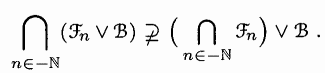
Publications marked with have appeared in refereed journals.

Last modification of static code: 2020-09-06
Last modification of list of publications: 2024-12-09
(webadmin)