Séminaire Lotharingien de Combinatoire, B53e (2006), 16 pp.

David Callan

Some Bijections and Identities for the Catalan and Fine Numbers

Abstract. We establish combinatorial interpretations of several identities for the Catalan and Fine numbers. Analytic proofs are outlined and we also give combinatorial proofs utilizing some new bijections of independent interest. We show that 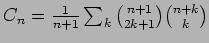$ C_{n}=\frac{1}{n+1}\sum_{k}\binom{n+1}{2k+1} \binom{n+k}{k}$ counts ordered trees on n edges by number of interior vertices adjacent to a leaf and 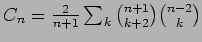$ C_{n}=\frac{2}{n+1}\sum_{k}\binom{n+1}{k+2} \binom{n-2}{k}$ counts Dyck n-paths by number of long interior inclines. We also give an analogue for the Fine numbers of Touchard's Catalan number identity.

Received: February 17, 2005. Accepted: January 4, 2006. Final Version: February 22, 2006.

The following versions are available: