Séminaire Lotharingien de Combinatoire, B54Af (2006), 29 pp.
Cristina M. Ballantine and Rosa C. Orellana
A Combinatorial Interpretation for the Coefficients
in the Kronecker Product
s(n-p,p)*s\lambda
Abstract.
In this paper we give a combinatorial interpretation for the coefficient of
s\nu in the Kronecker product
s(n-p,p)*s\lambda,
where \lambda=(\lambda1,
..., \lambdal(\lambda)) is a
partition
of n, if l(\lambda)>=2p-1 or
\lambda1>=2p-1;
that is, if \lambda is not a partition inside the
2(p-1) x 2(p-1) square.
For \lambda inside the square our combinatorial interpretation provides
an upper bound for the coefficients. In general, we are able to combinatorially
compute these coefficients for all \lambda when
n>(2p-2)2. We use this combinatorial
interpretation to give characterizations for multiplicity free Kronecker products. We have
also obtained some formulas for special cases.
Received: October 10, 2005.
Accepted: September 1, 2006.
Final Version: September 6, 2006.
The following versions are available:
Corrigendum
On page 25, line -6, in Corollary 4.13,
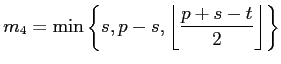 should be
replaced by
should be
replaced by
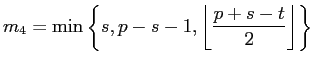 .
.
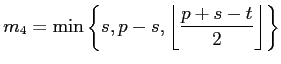
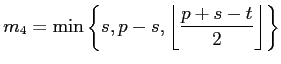 should be
replaced by
should be
replaced by
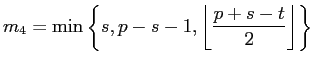 .
.