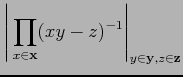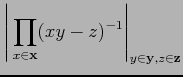Séminaire Lotharingien de Combinatoire, B61Ai (2010), 6 pp.
Alain Lascoux
Generalization of Scott's Permanent Identity
Abstract.
Let x={x1,...,xr},
y={y1,...,yn},
z={z1,...,zn}
be three sets of indeterminates.
We give the value of the determinant
when specializing y and z to the set of roots of
yn-1 and
zn-ξn, respectively.
Received: March 2, 2010.
Accepted: April 13, 2010.
The following versions are available: