Séminaire Lotharingien de Combinatoire, B66a (2011), 27 pp.

Alin Bostan, Frédéric Chyzak, Mark van Hoeij and Lucien Pech

Explicit Formula for the Generating Series of Diagonal 3D Rook Paths

Abstract. Let an denote the number of ways in which a chess rook can move from a corner cell to the opposite corner cell of an n x n x n three-dimensional chessboard, assuming that the piece moves closer to the goal cell at each step. We describe the computer-driven discovery and proof of the fact that the generating series 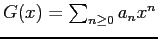$ G(x)= \sum_{n \geq 0} a_n x^n$ admits the following explicit expression in terms of a Gaussian hypergeometric function:

$\displaystyle G(x) = 1 + 6 \cdot \int_0^x \frac{ \,\pFq21{1/3}{2/ 3}{2} {\frac{27 w(2-3w)}{(1-4w)^3}}}{(1-4w)(1-64w)} \, dw. $


Received: May 18, 2011. Accepted: July 7, 2011. Final Version: October 4, 2011.

The following versions are available: