Séminaire Lotharingien de Combinatoire, B68a (2012), 20 pp.

Sergey Kitaev and Jeffrey Remmel

Quadrant Marked Mesh Patterns in Alternating Permutations

Abstract. This paper is a continuation of the systematic study of the distribution of quadrant marked mesh patterns initiated in [J. Integer Sequences, 12 (2012), Article 12.4.7]. We study quadrant marked mesh patterns on up-down and down-up permutations, also known as alternating and reverse alternating permutations, respectively. In particular, we refine classical enumeration results of André [C. R. Acad. Sci. Paris 88 (1879), 965-967; J. Math. Pur. Appl. 7 (1881), 167-184] on alternating permutations by showing that the distribution with respect to the quadrant marked mesh pattern of interest is given by (sec(xt))1/x on up-down permutations of even length and by 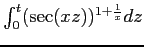$ \int_0^t (\sec(xz))^{1+\frac{1}{x}}dz$ on down-up permutations of odd length.

Received: May 2, 2012. Accepted: September 25, 2012. Final Version: September 28, 2012.

The following versions are available:

Corrigendum

On page 8, line 4 from the bottom, in the summation index UD2n(2k) should be replaced by DU2n(2k).

On page 9, line 2, in the summation index UD2n(2k) should be replaced by DU2n(2k+1).

On page 13, first line after (3.2), A2k+2(k+1)+k) should be replaced by A2k+2=((k+1)+k).

On page 19, line 10 above References, the definition of (x)n should be corrected to

(x)n=x(x+1)...(x+n-1)