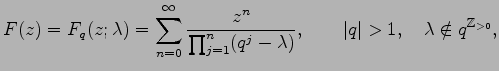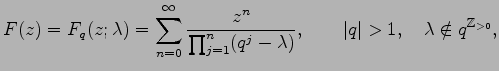This material has been published in Acta Arithm. 136 (2009), 243-269, the only definitive repository of the content that has been certified and accepted after peer review. Copyright and all rights therein are retained by the Polish Academy of Sciences. This material may not be copied or reposted without explicit permission.

Christian Krattenthaler, Igor Rochev, Keijo Väänänen and Wadim Zudilin

On the non-quadraticity of values of the q-exponential function and related q-series

(25 pages)

Abstract. We investigate arithmetic properties of values of the entire function
$\displaystyle F(z)=F_q(z;\lambda)=\sum_{n=0}^\infty\frac{z^n}{\prod_{j=1} ^n(q^j-\lambda)}, \qquad \vert q\vert>1, \quad \lambda\notin q^{\mathbb{Z}_{>0}}, $
that includes as special cases the Tschakaloff function (\lambda=0) and the q-exponential function (\lambda=1). In particular, we prove the non-quadraticity of the numbers Fq(\alpha;\lambda) for integral q, rational \lambda and \alpha not in -\lambda qZ>0, \alpha different from 0.

The following versions are available:

Back to Christian Krattenthaler's home page.