Die folgende Tabelle stellt einige Abbildungen R² → R² graphisch dar. Die 4 Spalten enthalten folgende Information.

1. Ein karteisches oder polares Netz und die Punkte gefärbt nach der Farbe des entsprechenden Bildpunkts. D.h. jene Farben die hier nicht vorkommen liegen nicht im Bild der Funktion (Funktion nicht surjektiv). Auf Punkten mit gleicher Farbe hat die Funktion gleiche Werte, ist also nicht injektiv.
   Anklicken lädt zwei Java-applets welche die Funktion in polar- und in Kartesischen Koordinaten darstellt und dem User durch Verschieben des weißen Punktes in der ersten Spalte, den entsprechenden schwarzen Bildpunkt in der dritten Spalte und den entsprechenden Wert der Determinante der Jacobi-Matrix in der vierten Spalte.
2. Die Definition der Funktion. Gezeichnet wird bisweilen eine gestreckte/verschobene Variante dieser Funktion.
3. Der Zielbereich der Funktion mit Farben entsprechend dem Farbkreis und den Bildern der Parameterlinien aus Spalte 1 unter der Funktion.
4. Niveaulinien der Determinante der Jacobimatrix und die Punkte gefärbt entsprechend der geographischen Höhe, d.h. in Punkte an der Grenze zwischen grün und blau ist die Determinante 0, also kein lokaler Diffeomorphismus. Bei blaune Punkten ist die Determinante negativ.

Definitionsbereich	Abbildung	WerteBereich	Determinante der Jacobimatrix
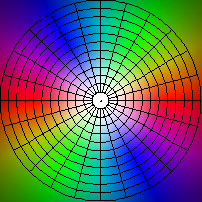
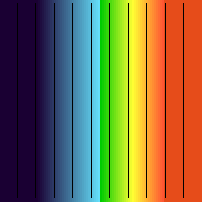
	z |-> z2
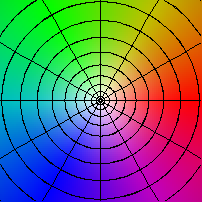
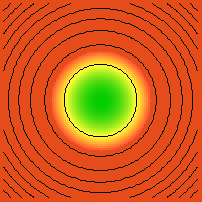
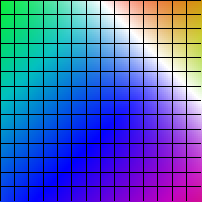
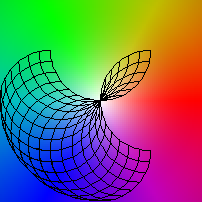
	(x,y) |-> (sin(x)-cos(y)+1, sin(y)-cos(x)+1)
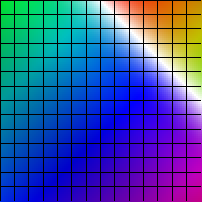
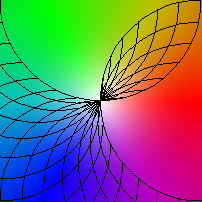
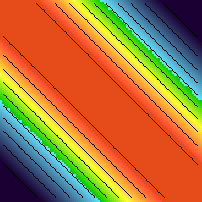
	(x,y) |-> (sin(x)-cos(y)+1, sin(y)-cos(x)+1)
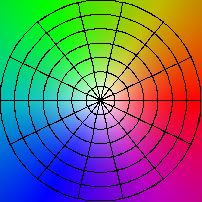
	(r,p) |-> (r cos(p), r sin(p))
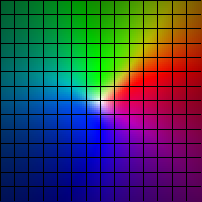
	(x,y) |-> (x+1/(1+y2)-1, y+1/(1+x2)-1)
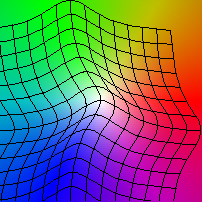
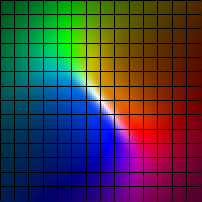
	(x,y) |-> (21/2x+sin(y), y+sin(x))
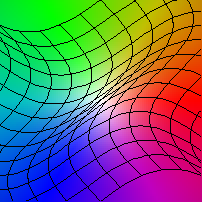
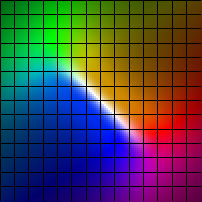
	(x,y) |-> (x+sin(y), y+sin(x))
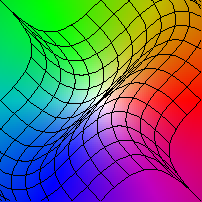
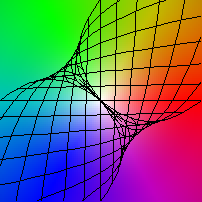
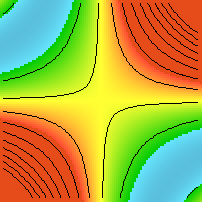
	(x,y) |-> (x+y x2, y+x y2)
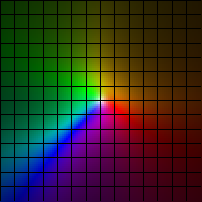
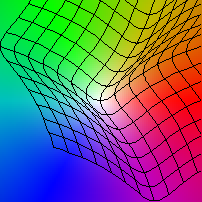
	(x,y) |-> (x+log(3+2y2), y+log(3+2x2))
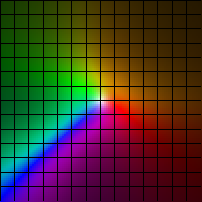
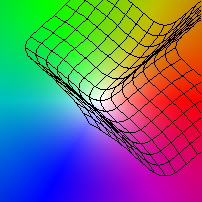
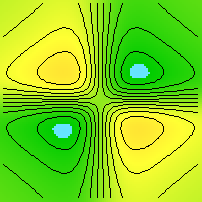
	(x,y) |-> 1.5(x/2+log(3+y2), y/2+log(5+x2))
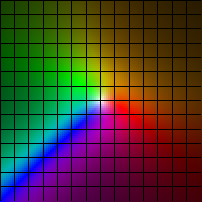
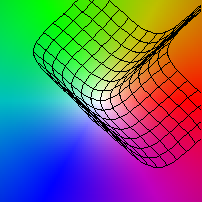
	(x,y) |-> 2(x/3+log(11+y2), y/3+log(11+x2))
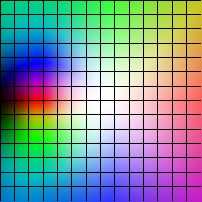
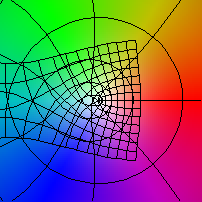
	z |-> z - (z3-1)/(3 z2)