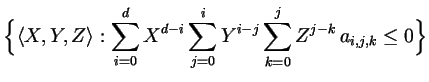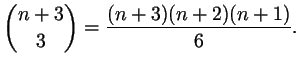5.3.5 Poly
The general object of this type of degree 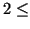 ORDER
ORDER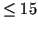 is
the poly object with syntax:
is
the poly object with syntax:
POLY:
poly { ORDER, < POLY_COEFFICIENTS > [POLY_MODIFIERS] }
POLY_COEFFICIENTS:
A quantity n of FLOATs separated by commas,
where n is ((ORDER+1)*(ORDER+2)*(ORDER+3))/6.
POLY_MODIFIERS:
[sturm [BOOL]] & [OBJECT_MODIFIERS]
See also:
It describes the object given by
where the coefficients are given in exactly this order.
Note that this is not the usual ordering by degree of homogeneity.
But the inverse lexicographical ordering of the sequence of exponents of 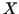 ,
, 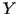 and
and 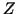 . Thus for degree 3 the 20 monomials are ordered as
. Thus for degree 3 the 20 monomials are ordered as
The number of coefficients of a polynomial of degree at most ORDER(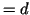 )
in the three variables
)
in the three variables 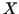 ,
, 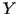 and
and 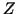 has as
many coefficients, as there are triples
has as
many coefficients, as there are triples 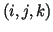 with
with
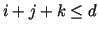 with
with
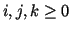 .
Such triple can be equally described by three numbers
.
Such triple can be equally described by three numbers
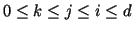 as in the sum above. Such 3 numbers can be viewed
as 3 separators at 3 different positions among
as in the sum above. Such 3 numbers can be viewed
as 3 separators at 3 different positions among 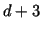 many items,
where
many items,
where 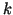 is the number of non-separators to the left of the first one,
is the number of non-separators to the left of the first one,
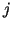 is that of non-separators to the left of the second and
is that of non-separators to the left of the second and
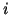 is that of non-separators to the left of the third one.
By combinatorics the number of such choices is
is that of non-separators to the left of the third one.
By combinatorics the number of such choices is
Andreas Kriegl 2003-07-23