Next: 4.2 Transformations Up: 4 Euclidean and Projective Previous: Links
The objects we want to display are situated in the space surrounding us.
We will neglect that this space is curved by gravitation according to
Einsteins general relativity theory (or 26 dimensional according to some quantum theoretic
approaches) and for sake of simplicity we may assume that this
is an affine 3-dimensional space. So after choosing some reference frame, i.e.
a zero-point and three independent vectors we may identify this space with the standard
3-dimensional vector space
![]() . Its points are uniquely given by 3 real coordinates
. Its points are uniquely given by 3 real coordinates
![]() denoted by
denoted by
![]() in Pov-Ray.
In Pov-Ray one may use as shortcut for a vector with equal coordinates
the real number given by this coordinate, e.g.
in Pov-Ray.
In Pov-Ray one may use as shortcut for a vector with equal coordinates
the real number given by this coordinate, e.g.
![]() .
The standard basis with respect to the given frame is denoted
.
The standard basis with respect to the given frame is denoted
Note that the second basic vector ![]() and not
and not ![]() is pointing up. The idea behind this choice ist
that usually we will project onto some
vertical plane, so the first two coordinates should be associated to this plane.
is pointing up. The idea behind this choice ist
that usually we will project onto some
vertical plane, so the first two coordinates should be associated to this plane.
On
![]() we have the usual
vector operations:
we have the usual
vector operations:
We will also make use of the inner product
![]() (denoted
(denoted
![]() in Pov-Ray)
of two vector
in Pov-Ray)
of two vector ![]() and
and ![]() , measuring essentially the angle
, measuring essentially the angle
![]() between the two vectors via
between the two vectors via
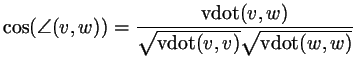
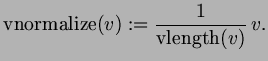
Andreas Kriegl 2003-07-23