Nächste Seite: 4 Integralrechnung Aufwärts: 3 Differenzierbare Funktionen Vorherige Seite: 3.2 Elementares über differenzierbare Inhalt Index
3.3.1 Definition.
Um ``stetig differenzierbar'' zu definieren, benötigen wir eine Distanz
auf
![]() . Eine
solche ist durch
. Eine
solche ist durch
![]() mit
mit
![]() gegeben.
Es ist
gegeben.
Es ist
![]() ein Euklidischer Raum falls
ein Euklidischer Raum falls
![]() einer ist.
einer ist.
Es heißt
![]() stetig differenzierbar (kurz
stetig differenzierbar (kurz
![]() ),
falls
),
falls
![]() für
alle
für
alle
![]() existiert und
existiert und
![]() stetig ist.
stetig ist.
Da
![]() bilinear und somit stetig ist
(
bilinear und somit stetig ist
(
![]() ) folgt aus der
Stetigkeit von
) folgt aus der
Stetigkeit von
![]() jene von
jene von
![]() .
.
Für endlich dimensionales
![]() gilt auch die Umkehrung, denn dann ist
gilt auch die Umkehrung, denn dann ist
![]() und aus der Stetigkeit von
und aus der Stetigkeit von
![]() folgt jene von
folgt jene von
![]() und somit auch von
und somit auch von
![]() (punktweise Konvergenz).
(punktweise Konvergenz).
3.3.2 Lemma.
Eine Abbildung
![]() ist genau dann
ist genau dann
![]() , wenn
die Richtungsableitungen eine wohldefinierte und stetige
Abbildung
, wenn
die Richtungsableitungen eine wohldefinierte und stetige
Abbildung
![]() ,
,
![]() liefern.
liefern.
Beweis.
![]() Wegen Proposition 3.1.9 müssen wir nur zeigen, daß
Wegen Proposition 3.1.9 müssen wir nur zeigen, daß
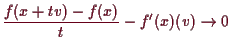 for
for 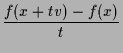 |
||
![\begin{multline*}
\Bigl\Vert\frac{f(x+tv)-f(x)}{t} - f'(x)(v) \Bigr\Vert \leq \\...
...a v)-d_vf(x)\Vert:0<\vartheta<1\} \leq \varepsilon .{\rm\quad[]}
\end{multline*}](img1299.png)
3.3.3 Proposition.
Ein Abbildung
![]() ist genau dann
stetig differenzierbar auf
ist genau dann
stetig differenzierbar auf
![]() , wenn
sämtliche partielle Ableitungen
, wenn
sämtliche partielle Ableitungen
![]() für
für
![]() existieren und stetig sind.
existieren und stetig sind.
Beweis.
![]() O.B.d.A. sei
O.B.d.A. sei
![]() und
und
![]() . Dann ist nach dem Mittelwertsatz
3.1.4
. Dann ist nach dem Mittelwertsatz
3.1.4
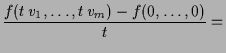 |
||
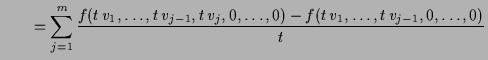 |
||
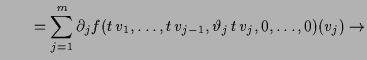 |
||
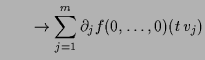 for for |
Wir wollen Gleichungen der Form
![]() nach
nach
![]() auflösen.
Sei also
auflösen.
Sei also
![]() eine Lösung. Falls nicht nur
eine Lösung. Falls nicht nur
![]() sondern auch
sondern auch
![]() differenzierbar ist, so gilt wegen
differenzierbar ist, so gilt wegen
![]() nach der Kettenregel
3.2.3
nach der Kettenregel
3.2.3
![]() . Wenn die Lösungen eindeutig
sind, d.h.
. Wenn die Lösungen eindeutig
sind, d.h.
![]() injektiv ist, dann ist wegen
injektiv ist, dann ist wegen
![]() auch
auch
![]() also
also
![]() und speziell für
und speziell für
![]() ist
ist
![]() , d.h.
, d.h.
![]() ist die inverse (lineare
Abbildung) zu
ist die inverse (lineare
Abbildung) zu
![]() .
.
Im endlich dimensionalen können wir die Invertierbarkeit linearer Abbildungen mit der Determinante testen.
Die Idee des folgenden Satzes ist, daß, wenn die Gleichung
![]() die durch die lineare Approximation
die durch die lineare Approximation
![]() gegeben ist,
eindeutig für alle
gegeben ist,
eindeutig für alle
![]() lösbar ist, dann sollte auch die nicht-lineare Gleichung
lösbar ist, dann sollte auch die nicht-lineare Gleichung
![]() für
für
![]() nahe
nahe
![]() eindeutig mit
eindeutig mit
![]() nahe
nahe
![]() lösbar sein.
lösbar sein.
3.3.4 Inverse-Funktionen Satz.
Es sei
![]()
![]() ,
,
![]() und
und
![]() ein Isomorphismus.
Dann ist
ein Isomorphismus.
Dann ist
![]() ein lokaler Diffeomorphismus, d.h. es gibt offene Umgebungen
ein lokaler Diffeomorphismus, d.h. es gibt offene Umgebungen
![]() von
von
![]() und
und
![]() von
von
![]() so daß
so daß
![]() bijektiv ist und die
Inverse
bijektiv ist und die
Inverse
![]()
![]() ist mit Ableitung
ist mit Ableitung
![]() .
.
Eine Menge
Beweis. Zuerst vereinfachen wir das Problem. Durch eine Translation (wir ersetzen
Es sei nun
![]() und
und
![]() .
Dann existiert für jedes
.
Dann existiert für jedes
![]() ein eindeutiges
ein eindeutiges
![]() mit
mit
![]() ,
also liegt
,
also liegt
![]() und
und
![]() ist bijektiv.
ist bijektiv.
Es ist
![]() (Lipschitz-)stetig,
denn für
(Lipschitz-)stetig,
denn für
![]() und
und
![]() mit
mit
![]() gilt:
gilt:
![]() ,
also
,
also
![]() .
.
Und schließlich ist
![]() differenzierbar, denn
differenzierbar, denn
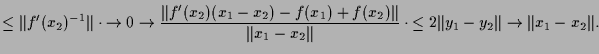 |
Daß
![]()
![]() ist folgt, da
ist folgt, da
![]() und alle Komponenten stetig sind.
[]
und alle Komponenten stetig sind.
[]
3.3.5 Beispiele.
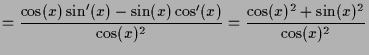 |
||
![$\displaystyle [f'(x,y)]=\begin{pmatrix}2x & -2y \\ 2y & 2x \end{pmatrix}$](img1389.png)
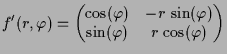
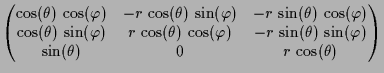
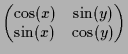
3.3.6 Implizite-Funktionen Satz.
Es sei
![]() lokal um
lokal um
![]()
![]() und
und
![]() ein Isomorphismus. Dann existieren offene Umgebungen
ein Isomorphismus. Dann existieren offene Umgebungen
![]() von
von
![]() ,
,
![]() von
von
![]() und
und
![]() von
von
![]() , so daß für jedes
, so daß für jedes
![]() und
und
![]() ein eindeutiges
ein eindeutiges
![]() existiert mit
existiert mit
![]() . Weiters ist die
Abbildung
. Weiters ist die
Abbildung
![]() ,
,
![]()
![]() .
.
Beachte, daß wir die Ableitungen von
Beweis. Es sei
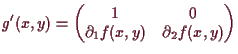
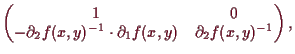
Nun wähle Umgebungen
![]() von
von
![]() und
und
![]() von
von
![]() mit
mit
![]() .
Dann ist für jedes
.
Dann ist für jedes
![]() und
und
![]() der Punkt
der Punkt
![]() , also
existiert ein eindeutiger Punkt
, also
existiert ein eindeutiger Punkt
![]() mit
mit
![]() , d.h.
, d.h.
![]() und
und
![]() , also ein eindeutiger Punkt
, also ein eindeutiger Punkt
![]() mit
mit
![]() .
Weiters ist
.
Weiters ist
![]() durch
durch
![]() gegeben, wobei
gegeben, wobei
![]() die Komponenten von
die Komponenten von
![]() bezeichnet. Folglich ist
diese Zuordnung
bezeichnet. Folglich ist
diese Zuordnung
![]() .
[]
.
[]
3.3.7 Beispiele.
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-3-05}\egroup](img1552.png)
Ohne die Lösungskurve
![]() explizit zu kennen, können wir durch
Differenzieren der impliziten Gleichung
explizit zu kennen, können wir durch
Differenzieren der impliziten Gleichung
![]() dennoch deren
Ableitung berechnen:
dennoch deren
Ableitung berechnen:
| 0 | ||
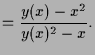 |
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-3-06}\egroup](img1553.png)
Der 1. Zylinder ist z.B. durch
![]() gegeben und der
2. Zylinder durch
gegeben und der
2. Zylinder durch
![]() .
Gesucht sind also die Lösungen der impliziten Gleichung
.
Gesucht sind also die Lösungen der impliziten Gleichung
![]() .
Die Ableitung von
.
Die Ableitung von ![]() ist
ist
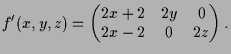
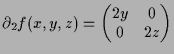 genau dann
invertierbar, wenn
genau dann
invertierbar, wenn
Um eine Nullstelle der (nicht-linearen) Gleichung
![]() zu erhalten
beginnen wir mit irgend einen Näherungswert
zu erhalten
beginnen wir mit irgend einen Näherungswert
![]() , betrachten
die affine Funktion
, betrachten
die affine Funktion
![]() die
die
![]() am besten approximiert, bestimmen ihre Nullstelle
am besten approximiert, bestimmen ihre Nullstelle
![]() , d.h. lösen
, d.h. lösen
![]() und erhalten als neue Näherungsnullstelle
von
und erhalten als neue Näherungsnullstelle
von
![]() den Punkt
den Punkt
![]() .
Das Newtonverfahren besteht nun darin auf rekursive Weise
.
Das Newtonverfahren besteht nun darin auf rekursive Weise
![]() zu definieren und zu hoffen, daß
zu definieren und zu hoffen, daß
![]() existiert, weil dann
existiert, weil dann
![]() , also
, also
![]() ist
(Verwende die stetige Differenzierbarkeit von
ist
(Verwende die stetige Differenzierbarkeit von
![]() und damit die Stetigkeit von
und damit die Stetigkeit von
![]() ).
Da aber die Bestimmung der Inversen
).
Da aber die Bestimmung der Inversen
![]() einer Matrix
einer Matrix
![]() sehr aufwendig ist, modifizieren wir dieses Verfahren derart, daß wir Anstelle von
sehr aufwendig ist, modifizieren wir dieses Verfahren derart, daß wir Anstelle von
![]() immer das fixe
immer das fixe
![]() verwenden und erhalten:
verwenden und erhalten:
3.3.8 Vereinfachtes Newtonverfahren.
Es sei
![]() stetig differenzierbar und
stetig differenzierbar und
![]() .
Es sei
.
Es sei
![]() invertierbar und es existiere ein
invertierbar und es existiere ein
![]() mit
mit
![]() für alle
für alle
![]() in einer offenen Menge
in einer offenen Menge
![]() .
Weiters sei
.
Weiters sei
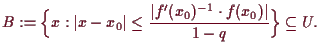
Beweis. Wir betrachten
3.3.9 Beispiel.
Die Menge der Startwerte, für die die Newtonfolge gegen eine fixe Nullstelle
konvergiert, ist im allgemeinen schwer beschreibbar.
Betrachten wir z.B. das Polynom
![]() als Abbildung
als Abbildung
![]() .
Dieses hat 3 komplexe Nullstellen
.
Dieses hat 3 komplexe Nullstellen
![]() ,
,
![]() .
Wir können es auch als Abbildung
.
Wir können es auch als Abbildung
![]() auffassen.
Die Ableitung von
auffassen.
Die Ableitung von
![]() ist gegeben durch (Multiplikation mit)
ist gegeben durch (Multiplikation mit)
![]() und die Newtonrekursion somit durch
und die Newtonrekursion somit durch
![]() .
Färben wir die Punkte der Ebene in 3 Farbe entsprechend den 3 Nullstellen
gegen welche die Newtonfolge mit diesen Startwerten konvergiert so erhalten wir
folgendes fraktales Bild, eine Juliamenge:
.
Färben wir die Punkte der Ebene in 3 Farbe entsprechend den 3 Nullstellen
gegen welche die Newtonfolge mit diesen Startwerten konvergiert so erhalten wir
folgendes fraktales Bild, eine Juliamenge:
![\bgroup\color{demo}\includegraphics[scale=.3]{julia-1}\egroup](img1554.png)
Wir werden später sehen, daß für die Konvergenz der
allgemeinen Newtonfolge die Bedingungen
![]() und
und
![]() für alle
für alle
![]() genügen.
In diesen Beispiel sind diese Bedingungen für
genügen.
In diesen Beispiel sind diese Bedingungen für
![]() und
und
![]() erfüllt.
erfüllt.
Andreas Kriegl 2001-07-01