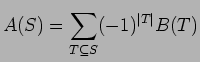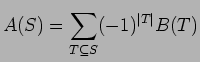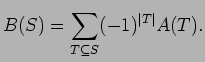Séminaire Lotharingien de Combinatoire, B54b (2005), 10 pp.

Ira M. Gessel

Symmetric Inclusion-Exclusion

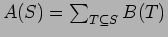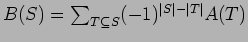Abstract. One form of the inclusion-exclusion principle asserts that if A and B are functions of finite sets then the formulas $ A(S) = \sum_{T\subseteq S}B(T)$ and $ B(S) = \sum_{T\subseteq S}(-1)^{\vert S\vert-\vert T\vert}A(T)$ are equivalent. If we replace B(S)$ by (-1)|S|B(S) then these formulas take on the symmetric form
$\displaystyle A(S) = \sum_{T\subseteq S}(-1)^{\vert T\vert}B(T)\\ $    

$\displaystyle B(S) = \sum_{T\subseteq S}(-1)^{\vert T\vert}A(T).$    
which we call symmetric inclusion-exclusion. We study instances of symmetric inclusion-exclusion in which the functions A and B have combinatorial or probabilistic interpretations. In particular, we study cases related to the Pólya-Eggenberger urn model in which A(S) and B(S) depend only on the cardinality of S.

Received: May 12, 2005. Accepted: July 20, 2005. Final Version: July 23, 2005.

The following versions are available: