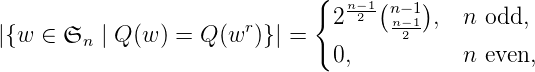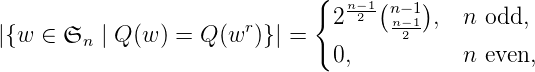Séminaire Lotharingien de Combinatoire, B86a (2022), 15 pp.
Tucker J. Ervin, Blake Jackson, Jay Lane, Kyungyong Lee, Son Dang Nguyen, Jack O'Donohue
and Michael Vaughan
Permutations whose Reverse Shares the Same Recording Tableau in the RS Correspondence
Abstract.
The RS correspondence is a bijection between permutations and pairs of standard Young tableaux with identical shape, where the tableaux are commonly denoted P (insertion) and Q (recording).
It has been an open problem to demonstrate
where wr is the reverse permutation of w.
First we show that for each w where Q(w) = Q(wr) the recording tableau Q(w) has a symmetric hook shape and satisfies a certain simple property.
From these two results, we succeed in proving the desired identity.
Received: September 30, 2021.
Revised: April 8, 2022.
Accepted: April 28, 2022.
Final Version: May 24, 2022.
The following versions are available: