Nächste Seite: 2 Grundlegende Algebra Aufwärts: Mathematik 1 für Informatik Vorherige Seite: Inhalt Inhalt Index
Aus dem Paradies [die Mengenlehre], das Cantor uns geschaffen hat, soll uns niemand mehr vertreiben können.Poincaré:
Spätere Generationen werden die Mengenlehre als Krankheit ansehen, die man überwunden hat.
In diesem ersten Abschnitt befassen wir uns mit der Sprache der Mathematik. Die natürlichen Sprachen wie deutsch, englisch, etc. mangelt es leider an der nötigen Präzision, insbesonders dann, wenn es darum geht unendliche Objekte und Prozesse zu beschreiben. Um die dadurch entstehenden Vieldeutigkeiten zu vermeiden wurde von Georg Cantor die Mengenlehre entwickelt.
1.1 Definition.
Unter einer Menge verstehen wir wie Cantor
eine Zusammenfassung wohlunterschiedener
Objekte unserer Anschauung oder unseres Denkens zu einem neuen Ganzen.
Es muß dabei im Prinzip feststellbar sein, ob ein gegebenes Objekt zur Menge
gehört oder nicht. Jene Objekte die zur Menge gehören heißen
Elemente der Menge.
Wenn ![]() eine Menge und
eine Menge und ![]() ein Objekt ist, dann schreiben wir
ein Objekt ist, dann schreiben wir
![]() falls
falls ![]() ein Element der Menge
ein Element der Menge ![]() ist und
ist und
![]() andernfalls.
Dies folgt der allgemeinen Methode in der Mathematik
die Negation einer Beziehung zweier Objekte durch Durchstreichen
des Relationssymbols zu bezeichnen, also
andernfalls.
Dies folgt der allgemeinen Methode in der Mathematik
die Negation einer Beziehung zweier Objekte durch Durchstreichen
des Relationssymbols zu bezeichnen, also
![]() bedeutet es ist nicht
bedeutet es ist nicht ![]() ,
sowie
,
sowie ![]() bedeutet
bedeutet ![]() ist ungleich (nicht gleich)
ist ungleich (nicht gleich) ![]() und
und ![]() bedeutet, daß
bedeutet, daß ![]() nicht kleiner als
nicht kleiner als ![]() ist.
ist.
Wir haben zwei Möglichkeiten Mengen ![]() zu beschreiben:
zu beschreiben:
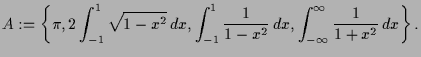
Insbesonders nennt man die Menge
![]() die kein einziges Element hat die
leere Menge. Beschreibend kann man sie auch durch Angabe einer Eigenschaft
die für kein
die kein einziges Element hat die
leere Menge. Beschreibend kann man sie auch durch Angabe einer Eigenschaft
die für kein ![]() erfüllt ist, wie z.B.
erfüllt ist, wie z.B. ![]() angeben, d.h.
angeben, d.h.
![]() .
.
Ein analoger Ausdruck, nämlich
![]() führt allerdings auf einen fatalen Widerspruch, denn
die Untersuchung der Frage ``Ist
führt allerdings auf einen fatalen Widerspruch, denn
die Untersuchung der Frage ``Ist ![]() ein Element von sich selbst oder
nicht?'' kann nur eine der beiden Antworten:
ein Element von sich selbst oder
nicht?'' kann nur eine der beiden Antworten: ![]() oder
oder
![]() haben. Im ersten Fall muß also
haben. Im ersten Fall muß also ![]() die definierende
Eigenschaft von
die definierende
Eigenschaft von ![]() besitzen, also
besitzen, also ![]() erfüllen im
Widerspruch zur Annahme. Im anderen Fall darf
erfüllen im
Widerspruch zur Annahme. Im anderen Fall darf ![]() die definierende
Eigenschaft von
die definierende
Eigenschaft von ![]() nicht besitzen, es darf also nicht
nicht besitzen, es darf also nicht ![]() gelten, und (wegen dem Satz vom ausgeschlossenen Dritten) muß
gelten, und (wegen dem Satz vom ausgeschlossenen Dritten) muß
![]() gelten, ebenfalls ein Widerspruch zur Annahme.
gelten, ebenfalls ein Widerspruch zur Annahme.
Auswege aus dem Widerspruch, den die Russel'sche Menge
![]() liefert, wurden viele ersonnen.
Grundidee dabei ist nicht alle Konstruktionen von Mengen zuzulassen.
liefert, wurden viele ersonnen.
Grundidee dabei ist nicht alle Konstruktionen von Mengen zuzulassen.
Die erste recht technische und heute überholte Methode wurde von
Russel und Whitehead in der Principia Mathematica präsentiert und
bestand darin Buchzuführen wie tief verschachtelt die Mengenklammern
einer Menge sind und jeweils nur solche eine Elemente einer
Menge von Tiefe ![]() zuzulassen, die selbst Tiefe
zuzulassen, die selbst Tiefe ![]() haben.
Dies ist aber sehr umständlich, und wollen wir ``Buchhaltern''
überlassen.
haben.
Dies ist aber sehr umständlich, und wollen wir ``Buchhaltern''
überlassen.
Zermelo, Fraenkel und Skolem sind ihrerseits so vorgegangen, daß nur mehr ganz bestimmte Konstruktionen, die wir in der Folge alle besprechen werden (wie z.B. Potenzmenge, Vereinigung, Durschnitt, etc.), verwendet werden dürfen um aus gegebenen Mengen neue zu definieren.
Eleganter ist der Zugang von Gödel, Bernays und Neumann,
die in der Beschreibung
![]() hat die Eigenschaft
hat die Eigenschaft ![]() wieder alle Eigenschaften
wieder alle Eigenschaften
![]() zulassen,
aber die so erhaltenen Objekte
zulassen,
aber die so erhaltenen Objekte ![]() nun Klassen oder Unmengen nennen, und nur deren Elemente als Mengen
bezeichnen. Ein Menge in ihren Sinn ist also eine Klasse, die in mindestens
einer Klasse als Element enthalten ist.
nun Klassen oder Unmengen nennen, und nur deren Elemente als Mengen
bezeichnen. Ein Menge in ihren Sinn ist also eine Klasse, die in mindestens
einer Klasse als Element enthalten ist.
Morse, Kelley und Tarski haben dies noch insofern modifiziert, daß die Einschränkung, daß alle Variablen in den bei der Klassenbildung betrachteten Aussagen nur Mengen durchlaufen dürfen, fallengelassen wurde. Für genauere Details dazu sei auf eine Vorlesung über Mengenlehre oder entsprechende Bücher verwiesen.
Zwei Mengen ![]() und
und ![]() sind genau dann gleich,
wenn sie genau die selben Elemente besitzen, d.h.
jedes beliebige Objekt
sind genau dann gleich,
wenn sie genau die selben Elemente besitzen, d.h.
jedes beliebige Objekt ![]() genau dann zu
genau dann zu ![]() gehört, wenn es zu
gehört, wenn es zu ![]() gehört.
Um dies kürzer symbolisieren zu können schreiben wir ``
gehört.
Um dies kürzer symbolisieren zu können schreiben wir ``![]() ''
statt ``für alle''.
Und wenn eine Aussage
''
statt ``für alle''.
Und wenn eine Aussage
![]() genau dann wahr ist wenn es eine Aussage
genau dann wahr ist wenn es eine Aussage
![]() ist,
so schreiben wir
ist,
so schreiben wir
![]() und sagen dafür
und sagen dafür
![]() ist äquivalent zu
ist äquivalent zu
![]() .
Wir können aus den Wahrheitswerten TRUE und FALSE
der beiden Teilaussagen
.
Wir können aus den Wahrheitswerten TRUE und FALSE
der beiden Teilaussagen
![]() und
und
![]() jene der (logischen) Äquivalenz
jene der (logischen) Äquivalenz
![]() bestimmen:
bestimmen:
|
|
|
|
| TRUE | TRUE | TRUE |
| FALSE | FALSE | TRUE |
| FALSE | TRUE | FALSE |
| TRUE | FALSE | FALSE |
Wenn schlußendlich ``:'' als ``(für die) gilt'' gelesen wird, dann
sind zwei Mengen ![]() und
und ![]() genau dann gleich
(d.h.
genau dann gleich
(d.h. ![]() ) wenn
) wenn
![]() ,
also
,
also
Eine schwächere Möglichkeit Mengen miteinander zu vergleichen ist folgende:
Eine Menge ![]() heißt Teilmenge einer Menge
heißt Teilmenge einer Menge ![]() (und wir schreiben dann
(und wir schreiben dann
![]() , oder sagen auch
, oder sagen auch ![]() ist Obermenge von
ist Obermenge von ![]() ),
genau dann, wenn jedes Element von
),
genau dann, wenn jedes Element von ![]() auch Element von
auch Element von ![]() ist.
Wenn eine Aussage
ist.
Wenn eine Aussage
![]() eine Aussage
eine Aussage
![]() zur Folge hat, so schreibt man
für diesen Sachverhalt
zur Folge hat, so schreibt man
für diesen Sachverhalt
![]() und sagt auch
und sagt auch
![]() impliziert
impliziert
![]() .
Es ist also
.
Es ist also
![]() selbst eine Aussage, die nur dann falsch sein kann,
wenn zwar
selbst eine Aussage, die nur dann falsch sein kann,
wenn zwar
![]() erfüllt ist, nicht aber
erfüllt ist, nicht aber
![]() .
Die Wahrheitstafel für ``
.
Die Wahrheitstafel für ``
![]() '' ist somit die folgende:
'' ist somit die folgende:
|
|
|
|
| TRUE | TRUE | TRUE |
| FALSE | FALSE | TRUE |
| FALSE | TRUE | TRUE |
| TRUE | FALSE | FALSE |
Beachte, daß
![]() genau dann gilt, wenn
sowohl
genau dann gilt, wenn
sowohl
![]() als auch
als auch
![]() (auch als
(auch als
![]() geschrieben)
gilt, d.h. die beiden
Aussagen
geschrieben)
gilt, d.h. die beiden
Aussagen
![]() und
und
![]() sich gegenseitig implizieren.
sich gegenseitig implizieren.
Wir können obige Definition nun kurz wie folgt schreiben:
Graphisch können wir das durch folgendes sogenanntes Venn-Diagramm veranschaulichen:
![\includegraphics[scale=0.5]{pic-1004}](img56.png)
Beachte, daß analog zu ![]() bei Zahlen für alle Mengen
bei Zahlen für alle Mengen ![]() die Aussage
die Aussage
![]() gilt. Will man nur echte Teilmengen
gilt. Will man nur echte Teilmengen
![]() betrachten, d.h.
welche
betrachten, d.h.
welche ![]() erfüllen, so schreiben wir dafür
erfüllen, so schreiben wir dafür
![]() (und sagt
(und sagt ![]() ist
eine echte Teilmenge von
ist
eine echte Teilmenge von ![]() ), d.h.
), d.h.
Für das Teilmengesein wird oft auch das Symbol
![]() anstelle
von
anstelle
von
![]() verwendet, da diese Situation in der Mathematik viel
öfter auftaucht als jene der echten Teilmenge (für die man dann
allerdings soetwas schreckliches wie
verwendet, da diese Situation in der Mathematik viel
öfter auftaucht als jene der echten Teilmenge (für die man dann
allerdings soetwas schreckliches wie
![]() B oder
B oder
![]() schreiben muß). Da man bei
Zahlen in der entsprechenden Situation aber auch
schreiben muß). Da man bei
Zahlen in der entsprechenden Situation aber auch ![]() und
nicht
und
nicht ![]() schreibt, will ich nicht so schreibfaul sein.
schreibt, will ich nicht so schreibfaul sein.
Offensichtlich ist ![]()
![]()
![]() und
und
![]() .
Diese Eigenschaft von
.
Diese Eigenschaft von ![]() heißt Antisymmetrie.
heißt Antisymmetrie.
Weiters folgt aus
![]() und
und
![]() die Aussage
die Aussage
![]() .
Mann nennt diese Eigenschaft die Transitivität von
.
Mann nennt diese Eigenschaft die Transitivität von ![]() .
.
Natürlich können Mengen selbst wieder Elemente einer Menge sein.
Z.B. können wir die Menge
![]() aller Teilmengen einer Menge
betrachten, also
aller Teilmengen einer Menge
betrachten, also
Beachte, daß sehr deutlich zu unterscheiden ist zwischen
![]() ,
,
![]() und
und ![]() .
Wenn
.
Wenn
![]() ,
, ![]() ,
,
![]() bezeichnet (Wer meint schon zu
wissen, was die Zahlen
bezeichnet (Wer meint schon zu
wissen, was die Zahlen
![]() sind, der möge andere Symbole für die 3
eben definierten Mengen verwenden), so ist
sind, der möge andere Symbole für die 3
eben definierten Mengen verwenden), so ist
1.2 Definition. Mengenoperationen.
Aus je zwei Mengen ![]() und
und ![]() können wir neue Mengen bilden:
können wir neue Mengen bilden:
Der Durchschnitt ![]() von
von ![]() und
und ![]() ist die Menge aller Objekte die sowohl
Elemente von
ist die Menge aller Objekte die sowohl
Elemente von ![]() als auch von
als auch von ![]() sind.
Salopp könnte man auch sagen: Der Durchschnitt besteht aus den Elementen die
in beiden Mengen liegen. Dies könnte allerdings zu Verwechslung mit der
weiter unten definierten Vereinigungsmenge führen, z.B.
wenn wir die Menge aller Studentinnen, die in beide parallel-Klassen gehen,
betrachten.
sind.
Salopp könnte man auch sagen: Der Durchschnitt besteht aus den Elementen die
in beiden Mengen liegen. Dies könnte allerdings zu Verwechslung mit der
weiter unten definierten Vereinigungsmenge führen, z.B.
wenn wir die Menge aller Studentinnen, die in beide parallel-Klassen gehen,
betrachten.
Wenn
![]() und
und
![]() zwei Aussagen sind, dann
bezeichnet man mit ``
zwei Aussagen sind, dann
bezeichnet man mit ``
![]() '' oder
'' oder
![]() die Aussage, daß beide Aussagen zutreffen.
In vielen Computersprachen wird `&&' anstelle des auf
der Tastatur nicht vorhandenen
die Aussage, daß beide Aussagen zutreffen.
In vielen Computersprachen wird `&&' anstelle des auf
der Tastatur nicht vorhandenen ![]() verwendet.
Man ließt dies als ``
verwendet.
Man ließt dies als ``
![]() und
und
![]() ''.
Die Wahrheitstafel
des (logischen) Unds
''.
Die Wahrheitstafel
des (logischen) Unds ![]() ist also folgende:
ist also folgende:
|
|
|
|
| TRUE | TRUE | TRUE |
| FALSE | FALSE | FALSE |
| FALSE | TRUE | FALSE |
| TRUE | FALSE | FALSE |
Es ist also
Dies kan man durch ein Venn-Diagramm veranschaulichen:
![\includegraphics[scale=0.7]{pic-1001}](img111.png)
Man sagt zwei Mengen ![]() und
und ![]() seien Element-fremd oder auch
disjunkt, wenn
seien Element-fremd oder auch
disjunkt, wenn
![]() , d.h. sie kein einziges
gemeinsames Element besitzen.
, d.h. sie kein einziges
gemeinsames Element besitzen.
Beachte, daß ![]() die größte gemeinsame Teilmenge von
die größte gemeinsame Teilmenge von ![]() und
und ![]() ist,
siehe auch (1.5).
ist,
siehe auch (1.5).
Beweis. Offensichtlich ist
Sei nun
![]() eine weitere gemeinsame Teilmenge von
eine weitere gemeinsame Teilmenge von
![]() und
und
![]() . Dann ist
. Dann ist
![]() (also
(also
![]() die größte gemeinsame Teilmenge), denn
aus
die größte gemeinsame Teilmenge), denn
aus
![]() folgt
folgt
![]() und
und
![]() also
also
![]() und somit
und somit
![]() .
[]
.
[]
Es ist
![]()
![]()
![]() .
.
Beweis. Aus
Die Vereinigung
![]() von
von
![]() und
und
![]() ist die Menge aller Objekte
die Element mindestens einer der beiden Mengen
ist die Menge aller Objekte
die Element mindestens einer der beiden Mengen
![]() bzw.
bzw.
![]() sind.
Wenn
sind.
Wenn
![]() und
und
![]() zwei Aussagen sind, dann
bezeichnet man mit
zwei Aussagen sind, dann
bezeichnet man mit
![]() die Aussage, daß zumindestens eine der beiden Aussagen zutrifft.
In vielen Computersprachen wird
die Aussage, daß zumindestens eine der beiden Aussagen zutrifft.
In vielen Computersprachen wird
![]() anstelle von
anstelle von
![]() .
Man liest dies als ``
.
Man liest dies als ``
![]() oder
oder
![]() '', muß dabei aber beachten, daß
dies ein nicht ausschließendes oder ist, also auch den Fall, daß
'', muß dabei aber beachten, daß
dies ein nicht ausschließendes oder ist, also auch den Fall, daß
![]() und
und
![]() gelten, inkludiert.
Interpretiere z.B. den Satz `Jack liebt Jill oder (Jack liebt) Jane''.
D.h. die Wahrheitstafel des (logischen) Oders
gelten, inkludiert.
Interpretiere z.B. den Satz `Jack liebt Jill oder (Jack liebt) Jane''.
D.h. die Wahrheitstafel des (logischen) Oders
![]() ist folgende:
ist folgende:
|
|
|
|
| TRUE | TRUE | TRUE |
| FALSE | FALSE | FALSE |
| FALSE | TRUE | TRUE |
| TRUE | FALSE | TRUE |
Es ist also
Auch dies kan man durch ein Venn-Diagramm veranschaulichen:
![\includegraphics[scale=0.7]{pic-1002}](img138.png)
Wir wollen nun die wichtigsten Rechenregeln für Durchschnitt und Vereinigung aufstellen:
1.3 Lemma.
Es seien
![]() ,
,
![]() und
und
![]() Mengen.
Dann gilt:
Mengen.
Dann gilt:
Kommutativität besagt also, daß wir bei der Durchschnitts- und Vereinigungsbildung die beiden Mengen miteinander vertauschen dürfen.
Assoziativität besagt also, daß
es ist egal ist, wie wir bei mehrfachen Vereinigungen oder
mehrfachen Durchschnitten Klammern setzen (in welcher Reihenfolge wir
sie also ausrechnen), und wir können
sie auch ganz weglassen, also
![]() oder
oder
![]() schreiben, ohne irgendwelche
Mißverständnisse zu provozieren.
schreiben, ohne irgendwelche
Mißverständnisse zu provozieren.
Distributivität zeigt,
daß wenn sich Durchschnitts- und Vereinigungsbildung abwechseln, so darf
man nicht mehr Klammern vertauschen, aber kann
![]() ``hineinmultiplizieren''. Vergleiche dies mit
dem Distributivgesetz für das Rechnen mit Zahlen:
``hineinmultiplizieren''. Vergleiche dies mit
dem Distributivgesetz für das Rechnen mit Zahlen:
![]() aber nicht
aber nicht
![]() .
.
Beweis. Wir geben verschiedene Beweise für das Distributivitätsgesetz
![\includegraphics[scale=0.7]{pic-1017}](img154.png)
1.4 Definition.
Wenn man anstelle zweier Mengen
![]() und
und
![]() endlich viele Mengen
endlich viele Mengen
![]() ,
,
![]() , ...,
, ...,
![]() gegeben hat, so kann
man rekursiv (siehe (3.4)) Durchschnitt und Vereinigung als
gegeben hat, so kann
man rekursiv (siehe (3.4)) Durchschnitt und Vereinigung als
Man schreibt kürzer und eindeutiger unter Vermeidung von ``
![]() '' auch
'' auch
![]() bzw.
bzw.
![]() für diese Mengen und
liest dies
als ``Durchschnitt/Vereinigung für
für diese Mengen und
liest dies
als ``Durchschnitt/Vereinigung für
![]() gleich 1 bis
gleich 1 bis
![]() der
der
![]() unten
unten
![]() ''.
''.
Will man das nun auf unendlich viele Mengen übertragen, also den
Durchschnitt
![]() oder die Vereinigung
oder die Vereinigung
![]() einer beliebigen Menge
einer beliebigen Menge
![]() von Mengen
von Mengen
![]() definieren, dann sollte wohl der Durchschnitt
definieren, dann sollte wohl der Durchschnitt
![]() die Menge all jener Objekte sein, die gleichzeitig in jeder
der Mengen
die Menge all jener Objekte sein, die gleichzeitig in jeder
der Mengen
![]() als Element enthalten sind, d.h.
als Element enthalten sind, d.h.
| und |
Wenn
![]() eine Eigenschaft für Mengen ist, so
benutzt man auch die Schreibweise
eine Eigenschaft für Mengen ist, so
benutzt man auch die Schreibweise
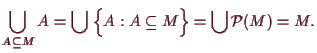
Wie für zweifache Vereinigung und Durchschnitt erhalten wir auch in dieser allgemeinen Situation:
1.5 Lemma.
Es sei
![]() eine nicht-leere Menge von Mengen.
Dann ist
eine nicht-leere Menge von Mengen.
Dann ist
![]() die kleinste (im Sinne von ``Teilmenge sein'') Menge,
die alle
die kleinste (im Sinne von ``Teilmenge sein'') Menge,
die alle
![]() als Teilmengen enthält.
als Teilmengen enthält.
Ebenso ist
![]() die größte (im Sinne von ``Teilmenge sein'') Menge,
die in allen
die größte (im Sinne von ``Teilmenge sein'') Menge,
die in allen
![]() enthalten ist.
enthalten ist.
Beweis. Für jedes
Sei nun
![]() eine Menge mit
eine Menge mit
![]() für alle
für alle
![]() . Dann ist
. Dann ist
![]() , denn aus
, denn aus
![]() folgt
folgt
![]() mit
mit
![]() und wegen
und wegen
![]() ist somit
ist somit
![]() .
.
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1023}\egroup](img550.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1024}\egroup](img551.png)
Sei andererseits
![]() eine Menge mit
eine Menge mit
![]() für alle
für alle
![]() .
Dann ist
.
Dann ist
![]() , denn aus
, denn aus
![]() folgt
folgt
![]() für alle
für alle
![]() , also
, also
![]() .
.
[]
1.6 Definition.
Unter der Differenzmenge
![]() zweier Mengen
zweier Mengen
![]() und
und
![]() (man sagt dafür auch:
(man sagt dafür auch:
![]() vermindert um
vermindert um
![]() )
versteht man die Menge aller Objekte
)
versteht man die Menge aller Objekte
![]() die zwar Elemente von
die zwar Elemente von
![]() nicht aber von
nicht aber von
![]() sind, d.h.
sind, d.h.
Das entsprechenden Venn-Diagramm ist:
![\includegraphics[scale=0.7]{pic-1003}](img228.png)
Wenn die Menge
![]() klar ist, d.h. sich alles in einer fixen Grundmenge
klar ist, d.h. sich alles in einer fixen Grundmenge
![]() abspielt, dann schreibt man auch kürzer
abspielt, dann schreibt man auch kürzer
![]() für
für
![]() und nennt
dies das Komplement von
und nennt
dies das Komplement von
![]() (in
(in
![]() ).
).
1.7 Proposition.
Sei
![]() eine Menge von Mengen
eine Menge von Mengen
![]() und
und
![]() eine weitere Menge.
Dann gelten:
eine weitere Menge.
Dann gelten:
Eine verbale Formulierung des links stehenden distributiv-Gesetzes ist: Ein Objekt liegt genau dann in
Eine graphische Darstellung der De Morgan'schen Gesetze ist:
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1021}\egroup](img552.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1022}\egroup](img553.png)
Eine verbale Formulierung ist:
Ein Objekt ist genau dann kein Element der Vereinigung, wenn
es in keinen der
![]() liegt.
Und ein Objekt ist genau dann kein Element des Durchschnitts, wenn
es in einen der
liegt.
Und ein Objekt ist genau dann kein Element des Durchschnitts, wenn
es in einen der
![]() nicht enthalten ist.
nicht enthalten ist.
Beweis. Es gilt:
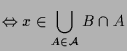 |
Um Beziehungen zwischen Objekten behandeln zu können, benötigen wir
eine Möglichkeit diese paarweise zusammenzufassen.
Natürlich könnten wir zu
![]() und
und
![]() die Menge
die Menge
![]() betrachten.
Wegen
betrachten.
Wegen
![]() ist das aber für Vergleiche
nicht geeignet, und wir brauchen
den Begriff des geordneten Paares
ist das aber für Vergleiche
nicht geeignet, und wir brauchen
den Begriff des geordneten Paares
![]() , der gewährleistet, daß
, der gewährleistet, daß
![\includegraphics[scale=0.6]{pic-1033}](img270.png)
Um also z.B. die Beziehung des Elternseins zu beschreiben
müßte man eine Tabelle, wo für jeden Menschen seine Eltern angeführt sind, aufstellen,
oder eine solche, wo für jeden Menschen alle seine Kinder angeführt sind,
oder für je zwei Menschen
![]() und
und
![]() angeben, ob
angeben, ob
![]() ein Kind von
ein Kind von
![]() (bzw.
(bzw.
![]() ein Elternteil von
ein Elternteil von
![]() ) ist.
D.h. in
) ist.
D.h. in
![]() sind alle Punkte
sind alle Punkte
![]() entsprechend mit den Werten
TRUE oder FALSE zu belegen. Es genügt natürlich dabei alle mit den Wert
TRUE anzugeben, also eine Teilmenge von
entsprechend mit den Werten
TRUE oder FALSE zu belegen. Es genügt natürlich dabei alle mit den Wert
TRUE anzugeben, also eine Teilmenge von
![]() auszuzeichnen.
Dies führt zu folgender
auszuzeichnen.
Dies führt zu folgender
1.8 Definition.
Eine Relation
![]() auf
auf
![]() ist eine Teilmenge von
ist eine Teilmenge von
![]() .
Man schreibt kürzer
.
Man schreibt kürzer
![]() anstelle von
anstelle von
![]() , und sagt dafür
, und sagt dafür
![]() steht in Relation
steht in Relation
![]() zu
zu
![]() .
Ist
.
Ist
![]() so spricht man kürzer (aber nicht ganz sauber)
von einer Relation auf
so spricht man kürzer (aber nicht ganz sauber)
von einer Relation auf ![]() .
.
Z.B. haben wir die Relationen
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() für Mengen, also auch auf der Potenzmenge
für Mengen, also auch auf der Potenzmenge
![]() jeder fix vorgegebenen
Menge
jeder fix vorgegebenen
Menge
![]() .
.
Wir können eine Relation auch mittels gerichteten Graph veranschaulichen, z.B.
für die Teilmengenrelation auf
![]() wobei wir
Pfeile die sich aus der Reflexivität ergeben nicht eingezeichnet sind:
wobei wir
Pfeile die sich aus der Reflexivität ergeben nicht eingezeichnet sind:
![\bgroup\color{demo}$\displaystyle \xymatrix{
\emptyset \ar@{->}[2,0] \ar@{->}[0,...
...{ 0\} \ar@{->}[2,
0] \\
& & \\
\{ 1\} \ar@{->}[0,2] & &\{ 0,1\} \\
} $\egroup](img282.png)
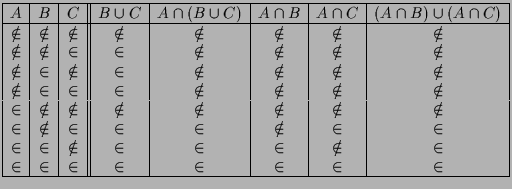
Auf folgende wichtige Eigenschaften können wir Relationen
![]() auf
auf
![]() untersuchen
untersuchen
Eine Relation heißt Äquivalenzrelation, wenn sie alle diese 3 Eigenschaften besitzt. Man schreibt dann oft
Äquivalenzrelationen sind zumeist dadurch gegeben, daß man Objekte äquivalent
nennt, wenn sie eine gewisse Eigenschaft gemein haben.
Z.B. ist für
![]() die Relation ``gleicher Rest bei Division durch
die Relation ``gleicher Rest bei Division durch
![]() ''
also
''
also
![]()
![]()
![]() teilt
teilt
![]() , d.h.
, d.h.
![]() :
:
![]() ,
eine Äquivalenzrelation auf
,
eine Äquivalenzrelation auf
![]() .
Ebenso sind ``gleicher Geburtstag'', ``gleiches Sternzeichen'',
``gleich viele Kinder'', ``gleiches Gewicht'', ``gleicher Vornamen'',
``in die gleiche Klasse gehen'' u.s.w.
Äquivalenzrelationen auf der Menge aller Menschen.
.
Ebenso sind ``gleicher Geburtstag'', ``gleiches Sternzeichen'',
``gleich viele Kinder'', ``gleiches Gewicht'', ``gleicher Vornamen'',
``in die gleiche Klasse gehen'' u.s.w.
Äquivalenzrelationen auf der Menge aller Menschen.
Beim letzten Beispiel, der in gleiche Klassen gehenden Schüler einer Schule,
steckt offensichtlich dahinter, daß die Schule (oder auch deren Schüler)
in Klassen eingeteilt sind. Wir wollen eine analoge Beschreibung nun für jede
Äquivalenzrelation
![]() auf Mengen
auf Mengen
![]() erhalten.
Dazu bezeichnen wir Mengen
erhalten.
Dazu bezeichnen wir Mengen
![]() , die bezüglich ``
, die bezüglich ``
![]() '' so groß wie möglich
(man sagt maximal) unter allen Teilmengen
'' so groß wie möglich
(man sagt maximal) unter allen Teilmengen
![]() sind welche nur
paarweise äquivalente Elemente enthalten, als Äquivalenzklassen der
Äquivalenzrelation
sind welche nur
paarweise äquivalente Elemente enthalten, als Äquivalenzklassen der
Äquivalenzrelation
![]() .
Wir verwenden dabei die Sprechweise ``paarweise äquivalenter'' anstelle
``äquivalenter'' Elemente, denn wir können ja jeweils nur
2 Elemente miteinander vergleichen um ihre Äquivalenz zu überprüfen und nicht
alle Elemente der Menge
.
Wir verwenden dabei die Sprechweise ``paarweise äquivalenter'' anstelle
``äquivalenter'' Elemente, denn wir können ja jeweils nur
2 Elemente miteinander vergleichen um ihre Äquivalenz zu überprüfen und nicht
alle Elemente der Menge
![]() auf einmal.
Wir können auch nicht von der größten Teilmenge mit obiger Eigenschaft
sprechen, denn man denke nur an die Klassen einer Schule, welche mehrere
maximale Mengen mit obiger Eigenschaft sind.
auf einmal.
Wir können auch nicht von der größten Teilmenge mit obiger Eigenschaft
sprechen, denn man denke nur an die Klassen einer Schule, welche mehrere
maximale Mengen mit obiger Eigenschaft sind.
Wie kann man nun Äquivalenzklassen finden? Man beginnt mit einen Element
![]() und betrachtet die Menge
und betrachtet die Menge
Diese Menge besteht offensichtlich aus paarweise äquivalenten Elementen,
denn wegen der Transitivität und Symmetrie sind
je zwei Elemente
![]() zueinander äquivalent.
Es kann auch keine echte Obermenge
zueinander äquivalent.
Es kann auch keine echte Obermenge
![]() mit dieser Eigenschaft geben,
denn deren Elemente müßten dann zu
mit dieser Eigenschaft geben,
denn deren Elemente müßten dann zu
![]() äquivalent sein.
Also ist
äquivalent sein.
Also ist
![]() eine Äquivalenzklasse von
eine Äquivalenzklasse von
![]() , die
einzige Klasse in der
, die
einzige Klasse in der
![]() als Element liegt, die
sogenannte von
als Element liegt, die
sogenannte von ![]() erzeugte Äquivalenzklasse.
erzeugte Äquivalenzklasse.
Umgekehrt ist jede Äquivalenzklasse
![]() von dieser Form, denn
kann
von dieser Form, denn
kann
![]() nicht leer sein, andernfalls wählen wir irgend ein
nicht leer sein, andernfalls wählen wir irgend ein
![]() und
erhalten eine größere Menge
und
erhalten eine größere Menge
![]() , einen Widerspruch
zur Maximalität.
Somit existiert ein
, einen Widerspruch
zur Maximalität.
Somit existiert ein
![]() und wir wählen ein solches.
Dann ist
und wir wählen ein solches.
Dann ist
![]() , da jedes
, da jedes
![]() zu
zu
![]() äquivalent ist und wegen der Maximalität von
äquivalent ist und wegen der Maximalität von
![]() ist
ist
![]() .
.
Es ist also
![]() gerade die Menge aller Äquivalenzklassen
von
gerade die Menge aller Äquivalenzklassen
von
![]() .
.
Die Äquivalenzklassen zur Teilbarkeit durch
![]() heißen
Restklassen modulo
heißen
Restklassen modulo ![]() , und man schreibt
, und man schreibt
![]() für die Menge
für die Menge
![]() der Restklassen ganzer Zahlen modulo
der Restklassen ganzer Zahlen modulo
![]() .
.
Beachte, daß sich hier unsere Vereinbarung, daß in der aufzählenden
Beschreibung einer Menge gleiche Elemente mehrfach auftreten dürfen
bezahlt macht, denn z.B. ist
![]() , denn als Reste
bei Division durch 2 kann ja nur
0 und
, denn als Reste
bei Division durch 2 kann ja nur
0 und
![]() auftreten.
auftreten.
1.9 Definition.
Eine Klasseneinteilung
![]() einer Menge
einer Menge
![]() ist eine Menge
ist eine Menge
![]() von nicht-leeren Teilmengen
von nicht-leeren Teilmengen
![]() die paarweise disjunkt sind
(d.h.
die paarweise disjunkt sind
(d.h.
![]() mit
mit
![]()
![]()
![]() )
und deren Vereinigung
)
und deren Vereinigung
![]() ist, d.h.
ist, d.h.
![]() .
.
1.10 Proposition.
Es sei
![]() eine nicht-leere Menge.
Dann entsprechen den Äquivalenzrelation
eine nicht-leere Menge.
Dann entsprechen den Äquivalenzrelation
![]() auf
auf
![]() genau den Klasseneinteilungen
genau den Klasseneinteilungen
![]() von
von
![]() .
.
Beweis. (
Sei weiters
![]() und
und
![]() .
Dann ist
.
Dann ist
![]() nach obigen.
nach obigen.
(
![]() )
Umgekehrt sei
)
Umgekehrt sei
![]() eine Klasseneinteilung von
eine Klasseneinteilung von
![]() .
Wir definieren
.
Wir definieren
![]()
![]()
![]() :
:
![]() .
Dies beschreibt eine Äquivalenzrelation
.
Dies beschreibt eine Äquivalenzrelation
![]() auf
auf
![]() :
:
Die Relation ist reflexiv, denn für
![]() existiert
eine
existiert
eine
![]() mit
mit
![]() , also
, also
![]() .
Sie ist offensichtlich symmetrisch. Nun zur Transitivität. Sei
.
Sie ist offensichtlich symmetrisch. Nun zur Transitivität. Sei
![]() , d.h.
, d.h.
![]() mit
mit
![]() ,
,
![]() . Also ist
. Also ist
![]() und somit
und somit
![]() , d.h.
, d.h.
![]() , also
, also
![]() .
.
Bleibt zu zeigen, daß das hin und her zwischen Äquivalenzrelationen
![]() und Klasseneinteilungen
und Klasseneinteilungen
![]() zusammenpaßt.
zusammenpaßt.
Sei also
![]() die Menge der Äquivalenzklassen einer Äquivalenzrelation
die Menge der Äquivalenzklassen einer Äquivalenzrelation
![]() und
und
![]() die aus
die aus
![]() gewonnene Äquivalenzrelation.
Wir behaupten, daß diese mit der ursprünglichen übereinstimmt.
Wir müssen also
gewonnene Äquivalenzrelation.
Wir behaupten, daß diese mit der ursprünglichen übereinstimmt.
Wir müssen also
![]() zeigen.
zeigen.
Sei zuerst
![]() , dann liegt
, dann liegt
![]() , also ist
auch
, also ist
auch
![]() nach Definition.
Umgekehrt sei
nach Definition.
Umgekehrt sei
![]() , d.h. es existiert ein
, d.h. es existiert ein
![]() mit
mit
![]() . Da
. Da
![]() aber aus bezüglich
aber aus bezüglich
![]() paarweise äquivalenten
Elementen
bestehen muß, ist
paarweise äquivalenten
Elementen
bestehen muß, ist
![]() .
.
Sei nun andererseits
![]() irgend eine Klasseneinteilung von
irgend eine Klasseneinteilung von
![]() und
und
![]() die zugehörige Äquivalenzrelation, d.h.
die zugehörige Äquivalenzrelation, d.h.
![]() .
Wir müssen zeigen, daß
.
Wir müssen zeigen, daß
![]() gerade aus den Äquivalenzklassen
gerade aus den Äquivalenzklassen
![]() von
von
![]() besteht.
besteht.
Es ist
![]() , denn für
, denn für
![]() ist
ist
![]() , also existiert ein
, also existiert ein
![]() mit
mit
![]() . Verschiedene
. Verschiedene
![]() liefern das gleiche
liefern das gleiche
![]() , denn die
, denn die
![]() sind nach Voraussetzung paarweise disjunkt.
Also ist
sind nach Voraussetzung paarweise disjunkt.
Also ist
![]() . Sei umgekehrt
. Sei umgekehrt
![]() . Dann ist
. Dann ist
![]() ,
also
,
also
![]() und damit
und damit
![]() .
.
Sei nun
![]() . Nach Voraussetzung ist
. Nach Voraussetzung ist
![]() , also können
wir ein
, also können
wir ein
![]() wählen. Dann ist aber wie zuvor
wählen. Dann ist aber wie zuvor
![]() , denn
, denn
![]() impliziert
impliziert
![]() und somit
und somit
![]() . Wegen der paarweisen Disjunktheit ist somit
. Wegen der paarweisen Disjunktheit ist somit
![]() .
[]
.
[]
1.11 Definition. Ordnungsrelationen.
Eine weitere wichtige Eigenschaft, auf die wir Relationen
![]() auf einer Menge
auf einer Menge
![]() untersuchen können,
ist die
Antisymmetrie, d.h.
untersuchen können,
ist die
Antisymmetrie, d.h.
![]() :
:
![]()
![]()
![]()
![]()
![]() .
.
Eine Relation die reflexiv, antisymmetrisch und transitiv ist heißt Ordnungsrelation (oder auch partielle Ordnung).
Ein Beispiel dafür ist die Relation
![]() für Mengen.
für Mengen.
Gilt zusätzlich die
Dichothomie
![]()
![]()
![]() ,
d.h. je zwei Elemente sind miteinander vergleichbar,
so heißt die Ordnung linear
oder auch totale Ordnung.
,
d.h. je zwei Elemente sind miteinander vergleichbar,
so heißt die Ordnung linear
oder auch totale Ordnung.
Ein Beispiel dafür ist die Relation
![]() für Zahlen.
für Zahlen.
Mittels solcher Relationen, können wir die Elemente einer Menge in eine Reihenfolge bringen.
Ordnungsrelationen auf einer endlichen Menge können wir
mittels sogenannten Hasse-Diagramm
veranschaulichen, wobei größere Elemente weiter oben stehen und
Verbindungen die sich aus Reflexivität oder Transitivität ergeben
nicht eingezeichnet werden.
Z.B. für die Teilmengenrelation auf
![]() :
:
![\bgroup\color{demo}$\displaystyle \xymatrix{
& &\{0,1,2\} & \\
\{0,1\}\ar@{-{}}...
...\
&\emptyset\ar@{-{}}[-2,0] \ar@{-{}}[-1,2] \ar@{-{}}[-1,-1] & & \\
} $\egroup](img372.png)
1.12 Definition. Funktionen.
Unter einer Abbildung (oder Funktion)
![]() von
von
![]() nach
nach
![]() (man schreibt
(man schreibt
![]() und nennt
und nennt
![]() den
Definitionsbereich und
den
Definitionsbereich und
![]() den Wertebereich von
den Wertebereich von
![]() )
versteht man eine Relation
)
versteht man eine Relation
![]() mit der Eigenschaft, daß
für jedes
mit der Eigenschaft, daß
für jedes
![]() genau ein
genau ein
![]() existiert mit
existiert mit
![]() (und man schreibt dann
(und man schreibt dann
![]() für dieses
für dieses
![]() oder auch
oder auch
![]() und
nennt es den Funktionswert von
und
nennt es den Funktionswert von
![]() bezüglich der Funktion
bezüglich der Funktion
![]() ).
Wir können uns eine Abbildung
).
Wir können uns eine Abbildung
![]() als Programm (oder besser als eine
blackbox)
vorstellen, welches für jeden Input
als Programm (oder besser als eine
blackbox)
vorstellen, welches für jeden Input
![]() einen wohldefinierten
Output
einen wohldefinierten
Output
![]() liefert.
liefert.
![\bgroup\color{demo}\includegraphics[scale=1]{pic-1025}\egroup](img554.png)
Wir schreiben
![]() für die Menge aller Abbildungen
für die Menge aller Abbildungen
![]() .
Die Motivation für diese Bezeichnungsweise ist, daß
.
Die Motivation für diese Bezeichnungsweise ist, daß
![]() für endliches
für endliches
![]() und
und
![]() gilt, siehe (3.23).
gilt, siehe (3.23).
Für Abbildungen
![]() und
und
![]() und
und
![]() ist das Bild von
ist das Bild von
![]() unter
unter
![]() definiert durch
definiert durch
![]()
![\bgroup\color{demo}\includegraphics[scale=1]{pic-1027}\egroup](img555.png)
und das Urbild von
![]() unter
unter
![]() definiert durch
definiert durch
![]() .
.
![\bgroup\color{demo}\includegraphics[scale=1]{pic-1028}\egroup](img556.png)
Man kann Abbildungen
![]() und
und
![]() zusammensetzen zu einer
Abbildung
zusammensetzen zu einer
Abbildung
![]() , die definiert ist durch
, die definiert ist durch
![]() .
Lies dies als ``g ring f'' oder ``g zusammengesetzt mit f''.
Als Teilmenge
.
Lies dies als ``g ring f'' oder ``g zusammengesetzt mit f''.
Als Teilmenge
![]() bedeutet dies
bedeutet dies
![\bgroup\color{demo}\includegraphics[scale=1]{pic-1026}\egroup](img557.png)
Wichtige Eigenschaften, auf die hin man Abbildungen
![]() untersuchen
kann, sind:
untersuchen
kann, sind:
![\bgroup\color{demo}\includegraphics[scale=1]{pic-1029}\egroup](img558.png)
![\bgroup\color{demo}\includegraphics[scale=1]{pic-1030}\egroup](img559.png)
Beispiel.
Wir betrachten die Funktion
![]() als Funktion zwischen folgenden Mengen
wobei
als Funktion zwischen folgenden Mengen
wobei
![]() bezeichnet:
bezeichnet:
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1031}\egroup](img560.png)
1.13 Bemerkung.
Die Notation
![]() für die Zusammensetzung von
für die Zusammensetzung von
![]() mit
mit
![]() ist keineswegs glücklich gewählt, denn dabei wirkt ja zuerst
ist keineswegs glücklich gewählt, denn dabei wirkt ja zuerst
![]() und dann
und dann
![]() auf einen Input
auf einen Input
![]() .
Würde man hier allerdings die Reihenfolge umdrehen, so
wäre es wegen der definierenden Formel
.
Würde man hier allerdings die Reihenfolge umdrehen, so
wäre es wegen der definierenden Formel
![]() zweckmäßig auch die rechte Seite besser als
zweckmäßig auch die rechte Seite besser als
![]() zu schreiben, d.h.
den Wert von
zu schreiben, d.h.
den Wert von
![]() bzgl. der Abbildung
bzgl. der Abbildung
![]() als
als
![]() und nicht
und nicht
![]() .
Dies würde auch durchwegs der Idee entsprechen, daß
ja
.
Dies würde auch durchwegs der Idee entsprechen, daß
ja
![]() genommen wird und darauf dann die Vorschrift
genommen wird und darauf dann die Vorschrift
![]() angewandt wird,
was auch der Schreibweise
angewandt wird,
was auch der Schreibweise
![]() entspricht.
Die Definition der Zusammensetzung wäre dann
entspricht.
Die Definition der Zusammensetzung wäre dann
![]() .
Allerdings ist dies fast allen MathematikerInnen doch eine zu radikale
Veränderung alteingessener Bezeichnungsweisen und es würde zweifellos
zu einem heillosen Durcheinander kommen, würden diese Bezeichnungsweise
gleichzeitig verwendet werden. Im Sinne der kulturellen Vielfalt
können wir wohl durchaus damit leben, daß Teile unserer Notation
halt nicht europäisch von links nach rechts laufend geschrieben werden.
Anhand vieler Beweise werden wir sowieso zum Schluß kommen, daß Mathematik
nicht linear von sich geht. In diesem Sinn
werden wir viele Relationssymbole in allen möglichen Orientierungen schreiben,
wie z.B.
.
Allerdings ist dies fast allen MathematikerInnen doch eine zu radikale
Veränderung alteingessener Bezeichnungsweisen und es würde zweifellos
zu einem heillosen Durcheinander kommen, würden diese Bezeichnungsweise
gleichzeitig verwendet werden. Im Sinne der kulturellen Vielfalt
können wir wohl durchaus damit leben, daß Teile unserer Notation
halt nicht europäisch von links nach rechts laufend geschrieben werden.
Anhand vieler Beweise werden wir sowieso zum Schluß kommen, daß Mathematik
nicht linear von sich geht. In diesem Sinn
werden wir viele Relationssymbole in allen möglichen Orientierungen schreiben,
wie z.B.
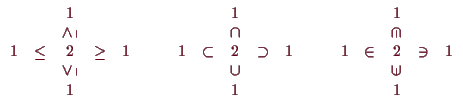
Auch die Bezeichnung
![]() für die Bildmenge und
für die Bildmenge und
![]() für
Urbildmenge ist mit
Vorsicht zu geniesen, denn wenn
für
Urbildmenge ist mit
Vorsicht zu geniesen, denn wenn
![]() eine Abbildung ist
dann kann für eine Teilmenge
eine Abbildung ist
dann kann für eine Teilmenge
![]() gleichzeitig auch
gleichzeitig auch
![]() gelten und somit kann die Bildmenge
gelten und somit kann die Bildmenge
![]() und der Funktionswert
und der Funktionswert
![]() etwas ganz verschiedenes sein.
Wenn man dazuschreibt, ob man
etwas ganz verschiedenes sein.
Wenn man dazuschreibt, ob man
![]() oder
oder
![]() betrachtet, so ist
allerdings eine Mißverständnis ausgeschlossen.
betrachtet, so ist
allerdings eine Mißverständnis ausgeschlossen.
Die grundlegenden Eigenschaften von Bild und Urbild faßt folgende Proposition zusammen:
1.14 Proposition.
Es sei
![]() eine Abbildung,
eine Abbildung,
![]() ,
,
![]() ,
,
![]() und
und
![]() . Dann gilt:
. Dann gilt:
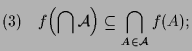 |
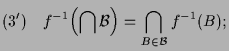 |
|||
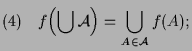 |
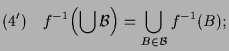 |
|||
Visualisieren kann man diese Aussagen folgendermaßen:
![\includegraphics[scale=0.6]{pic-1032a}](img432.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1032b}\egroup](img561.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1032c}\egroup](img562.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1032d}\egroup](img563.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1032e}\egroup](img564.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1032f}\egroup](img565.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1032g}\egroup](img566.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1032h}\egroup](img567.png)
Verbale Formulierungen sind z.B.:
Beweis. (0)
(1)
![]() nach (0), da
nach (0), da
![]() .
.
(2) Sei
![]() ,
,
![]() , d.h.
, d.h.
![]() .
Somit ist
.
Somit ist
![]() und damit
und damit
![]() .
.
(3)
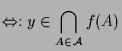 |
(4)
 |
(5')
Beachte, daß in (3) nicht Gleichheit gilt: Es sei
![]() die Funktion
die Funktion
![]() ,
,
![]() und
und
![]() .
Dann ist
.
Dann ist
![]() , aber
, aber
![]() und
somit auch
und
somit auch
![]() .
.
Der Grund warum der Beweis für Gleichheit nicht funktioniert ist,
daß zwar ``es gibt ein
![]() , sodaß für alle
, sodaß für alle
![]() eine Aussage gilt''
zur Folge hat, daß ``für jedes
eine Aussage gilt''
zur Folge hat, daß ``für jedes
![]() ein
ein
![]() existiert, sodaß dieselbe Aussage
gilt'' jedoch nicht umgekehrt.
Man vergleiche z.B.
``Jeder Mensch besitzt eine Mutter'' mit ``Es gibt eine Frau die Mutter von
jedem Menschen ist''.
Oder auch ``jeder wird von jemanden geliebt'' im Gegensatz zu
``Es gibt jemanden der jeden liebt''.
existiert, sodaß dieselbe Aussage
gilt'' jedoch nicht umgekehrt.
Man vergleiche z.B.
``Jeder Mensch besitzt eine Mutter'' mit ``Es gibt eine Frau die Mutter von
jedem Menschen ist''.
Oder auch ``jeder wird von jemanden geliebt'' im Gegensatz zu
``Es gibt jemanden der jeden liebt''.
1.16 Proposition.
Es sei
![]() eine Abbildung und
eine Abbildung und
![]() .
Dann gilt:
.
Dann gilt:
Beweis. (1) (
(
![]() ) Umgekehrt sei
) Umgekehrt sei
![]() und
und
![]() . Dann ist
. Dann ist
![]() , also
, also
![]() injektiv.
injektiv.
(2) (
![]() ) Sei nun
) Sei nun
![]() surjektiv. Für jedes
surjektiv. Für jedes
![]() wählen wir ein
zugehöriges
wählen wir ein
zugehöriges
![]() (Das dies wirklich möglich ist, ist das
Auswahlaxiom der Mengenlehre)
und setzen
(Das dies wirklich möglich ist, ist das
Auswahlaxiom der Mengenlehre)
und setzen
![]() . Dann ist
. Dann ist
![]() eine wohldefinierte Funktion
mit
eine wohldefinierte Funktion
mit
![]() .
.
(
![]() ) Umgekehrt sei
) Umgekehrt sei
![]() und
und
![]() . Es ist
. Es ist
![]() und
und
![]() , d.h.
, d.h.
![]() ist surjektiv.
ist surjektiv.
(3) (
![]() ) Entweder man
definiert
) Entweder man
definiert
![]() und rechnet leicht nach, daß
diese Relation eine Abbildung ist, welche invers zu
und rechnet leicht nach, daß
diese Relation eine Abbildung ist, welche invers zu
![]() ist, oder
man verwendet (1) und (2) und erhält ein
linksinverses
ist, oder
man verwendet (1) und (2) und erhält ein
linksinverses
![]() und ein rechtsinverses
und ein rechtsinverses
![]() . Dann ist
. Dann ist
(
![]() ) Dies folgt sofort aus (1) und (2).
[]
) Dies folgt sofort aus (1) und (2).
[]
1.15 Bemerkung.
Die eindeutige Abbildung
![]() mit
mit
![]() und
und
![]() ,
die für bijektive
,
die für bijektive
![]() existiert, heißt Umkehrfunktion von
existiert, heißt Umkehrfunktion von ![]() oder auch inverse Funktion zu
oder auch inverse Funktion zu ![]() und wird auch als
und wird auch als
![]() bezeichnet.
bezeichnet.
Falls
![]() bijektiv ist, so ist das Urbild
bijektiv ist, so ist das Urbild
![]() von
von
![]() bzgl. der
Funktion
bzgl. der
Funktion
![]() gerade das Bild von
gerade das Bild von
![]() bzgl. der Umkehrfunktion
bzgl. der Umkehrfunktion
![]() von
von
![]() . Beachte jedoch, daß
. Beachte jedoch, daß
![]() auch dann definiert ist, wenn
auch dann definiert ist, wenn
![]() als Abbildung nicht existiert.
als Abbildung nicht existiert.
1.17 Definition.
Es sei
![]() eine Abbildung und
eine Abbildung und
![]() eine Teilmenge.
Unter der Einschränkung
eine Teilmenge.
Unter der Einschränkung
![]() verstehen wir die Abbildung
verstehen wir die Abbildung
![]() , die
auf
, die
auf
![]() mit
mit
![]() übereinstimmt, also durch
übereinstimmt, also durch
![]() gegeben ist.
Als Teilmenge von
gegeben ist.
Als Teilmenge von
![]() ist also
ist also
![]() .
.
![\includegraphics[scale=0.7]{pic-1015}](img505.png)
1.18
Um Mengen der Größe nach miteinander vergleichen zu können, können wir für
endliche Mengen natürlich die Anzahlen der Elemente bestimmen und diese dann
vergleichen. Ohne wirklich zählen zu können gibt es aber auch eine
andere Möglichkeit:
Um z.B. festzustellen, ob gleichviele HöhrerInnen wie Sitzplätze vorhanden
sind, bittet man darum, daß sich alle setzten und falls weder leere Sitze
überbleiben noch Personen stehenbleiben, dann sind es gleich viele.
Mathematisch kann man das so beschreiben, daß versucht wird jeder Person
![]() einen Platz
einen Platz
![]() so zuzuordnen, daß keine zwei Personen den gleichen Platz
angewiesen bekommen und auch kein Platz übrigbleibt, d.h. diese Zuordnung
so zuzuordnen, daß keine zwei Personen den gleichen Platz
angewiesen bekommen und auch kein Platz übrigbleibt, d.h. diese Zuordnung
![]() von der Menge aller Personen in die Menge aller Plätze bijektiv ist.
Dieses Verfahren können wir auch bei unendlichen Mengen durchführen und geben dazu folgende
von der Menge aller Personen in die Menge aller Plätze bijektiv ist.
Dieses Verfahren können wir auch bei unendlichen Mengen durchführen und geben dazu folgende
Definition.
Wir schreiben
![]() (oder auch
(oder auch
![]() ),
falls
),
falls
![]() und
und
![]() gleichmächtig sind, d.h. eine bijektive Abbildung
gleichmächtig sind, d.h. eine bijektive Abbildung
![]() existiert.
Eine Menge
existiert.
Eine Menge
![]() heißt abzählbar (unendlich) falls sich gleichmächtig mit der Menge
heißt abzählbar (unendlich) falls sich gleichmächtig mit der Menge
![]() der natürlichen Zahlen ist.
der natürlichen Zahlen ist.
Eine Menge heißt endlich, falls sie nur endlich viele Elemente besitzt,
also
gleichmächtig zu einer natürlichen Zahl
![]() ist.
ist.
1.19 Bemerkung.
Im Unterschied zu endlichen Mengen, kann eine unendliche Menge durchaus
gleichmächtig mit einer echten Teilmenge sein.
Z.B. definiert
![]() eine bijektive Abbildung
eine bijektive Abbildung
![]() .
.
Veranschaulichen kann man sich dies wie folgt: Man betrachtet Hilbert's Hotel, ein Hotel mit abzählbar unendlich vielen Zimmern, die mit den natürlichen Zahlen 0,1,2,...durchnumeriert sind. Diese Hotel sei voll belegt und es kommt ein neuer Gast, welcher dadurch untergebracht werden kann, daß man die bereits einquartierten Gäste bittet jeweils in das Zimmer mit der nächst höheren Nummer zu wechseln und somit Zimmer 0 freibekommt.
Man kann sogar eine unendliche Teilmenge entfernen ohne die
Gleichmächtigkeit zu stören:
Betrachte die Menge
![]() der gerade Zahlen.
Dann definiert
der gerade Zahlen.
Dann definiert
![]() eine bijektive Abbildung
eine bijektive Abbildung
![]() . Und für die Menge
. Und für die Menge
![]() der ungeraden
Zahlen gilt ebenfalls
der ungeraden
Zahlen gilt ebenfalls
![]() vermöge
vermöge
![]() .
Es ist also
.
Es ist also
![]() die disjunkte Vereinigung
die disjunkte Vereinigung
![]() und beide Teilmengen sind gleichmächtig mit
und beide Teilmengen sind gleichmächtig mit
![]() .
.
Ebenso ist
![]() , denn
, denn
![]() und
und
![]() sowie
sowie
![]() ,
also
,
also
![]() nach
Übungsaufgabe (43).
nach
Übungsaufgabe (43).
Veranschaulichen kann man sich das wieder durch Hilbert's Hotel. Diesmal kommt ein Reisebus mit abzählbar unendlich vielen Passagieren die alle untergebracht werden sollen. Diesmal werden die bereits einquartierten Gäste gebeten jeweils in das Zimmer mit der doppelt so großen Nummer zu wechseln. Dann werden alle Zimmer mit ungerader Nummer frei und wir können die Passagiere des Reisebusses in diesen abzählbar unendlich vielen Zimmern unterbringen.
Aber auch
![]() ist abzählbar. Dazu numeriere man die Punkte in
ist abzählbar. Dazu numeriere man die Punkte in
![]() wie folgt:
wie folgt:
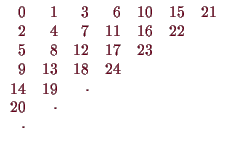
Das bedeutet also, daß selbst wenn auf abzählbar unendlich vielen Welten
jeweils ein voll belegtes Hotel von Hilbert steht und aus Einsparungsgründen
alle bis auf ein Hotel aufgelöst werden sollen, dann kann man den Gästen,
die durch Hotelnummer und Zimmernummer beschrieben werden können (also durch
Punkte in
![]() ), auf eindeutige Weise neue Zimmernummern in
), auf eindeutige Weise neue Zimmernummern in
![]() des
verbleibenden Hotels zuweisen.
des
verbleibenden Hotels zuweisen.
In Übungsaufgabe (44) werden wird zeigen, daß die Menge aller endlichen Folgen natürlicher Zahlen ebenfalls abzählbar ist, und somit auch die Menge der Polynome mit rationalen Koeffizienten und ebenso die Menge der algebraischen Zahlen, d.h. Nullstellen solcher Polynome. Aus dem gleichen Argument ist auch die Menge aller möglichen (endlich langen) Worte (die mittels Buchstaben aus einen abzählbaren Alphabet gebildet werden können) abzählbar und ebenfalls die Menge aller mögliche (endlichen) Sätze und genauso aller (endlichen) Bücher.
Daß es aber auch echt mächtigere unendliche Mengen (sogenannte überabzählbare Mengen) gibt, war eine von Cantor's wesentlichen Erkenntnissen:
1.20 Proposition.
Es sei
![]() eine Menge. Dann ist die Potenzmenge
eine Menge. Dann ist die Potenzmenge
![]() nicht
gleichmächtig mit
nicht
gleichmächtig mit
![]() .
.
Offensichtlich definiert
Beweis. Angenommen es gäbe eine surjektive Abbildung
Bemerkung.
Ähnlich zeigt man, daß die Menge der reellen Zahlen nicht abzählbar ist.
1.21 Definition.
Es sei
![]() eine Menge von Mengen.
Unter dem Produkt
eine Menge von Mengen.
Unter dem Produkt
![]() versteht man die Menge
versteht man die Menge
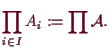
Andreas Kriegl 2002-02-01