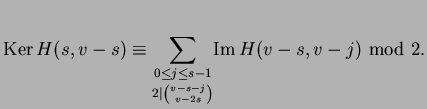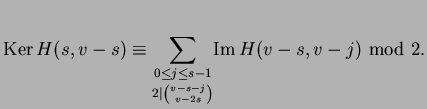Séminaire Lotharingien de Combinatoire, B45d (2001), 18 pp.
Helmut Krämer
Binary Moore-Penrose Inverses of
Set Inclusion Incidence Matrices
Abstract.
This note is a supplement to some recent work of R. B. Bapat
on Moore-Penrose inverses of set inclusion matrices.
Among other things Bapat
constructs these inverses (in case of existence)
for H(s,k) mod p, p
an arbitrary prime,
0 <= s <= k <= v-s.
Here we restrict ourselves to p=2. We give conditions
for s,k which are easy to state
and which ensure that the Moore-Penrose inverse of
H(s,k) mod 2 equals its transpose.
E.g., H(s,v-s) mod 2
has this property. Furthermore
Ker H(s,v-s) mod 2 is nonzero if
0 < 2s < v <= 3s
and then there is a decomposition
Also, refinements of this decomposition are given.
Received: December 14, 2000; Accepted: March 9, 2001.
The following versions are available: