Lösung für Aufgabe 5.2.55
Zeigen Sie, dass die Menge aller invertierbaren Abbildungen einer beliebigen Menge $M$ auf sich selbst eine Gruppe bildet. Ist die Menge endlich mit $n$ Elementen, dann nennen wir die entstehende Gruppe die Permutationsgruppe mit $n$ Elementen und bezeichnen sie mit $\mathfrak S_n$. Bestimmen Sie die Cayley–Tafeln von $\mathfrak S_1$, $\mathfrak S_2$ und $\mathfrak S_4$.Wir wissen aus Kapitel 4, dass die Zusammensetzung von Abbildungen assoziativ ist. Die Identität $id_M$ auf $M$ ist bijektiv und das Einselement. Weil jede Abbildung $f$ bijektiv ist, existiert die Umkehrabbildung $f^{-1}$, die Inverse zu $f$ bezüglich der Verknüpfung. Daher sind die Gruppeneigenschaften erfüllt. Die einelementige Menge besitzt nur eine Permutation, die Identität. Die zweielementige Menge besitzt die Identität und die Transposition $\si$, die die beiden Elemente vertauscht. Es gibt $24=4!$ Permutationen der vierelementigen Menge. Um diese eindeutig zu bezeichnen, führen wir die Zyklenschreibweise für Permutationen ein: Wenn wir z.B. $(a\,b\,c\,d)$ schreiben, dann bezeichnen wir damit die Abbildung $a\mapsto b$, $b\mapsto c$, $c\mapsto d$, $d\mapsto a$ und $x\mapsto x$ für $x\neq a,b,c,d$. Schreiben wir mehrere solche Klammern nebeneinander, z.B. $(a\,b\,c)(u\,v)$, dann bezeichnet das die Abbildung $a\mapsto b$, $b\mapsto c$, $c\mapsto a$, $u\mapsto v$, $v\mapsto u$ und $x\mapsto x$ für $x\neq a,b,c,d,u,v$. Die Cayley--Tafeln sind:
- $\mathfrak S_1$:
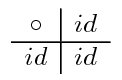
- $\mathfrak S_2$:
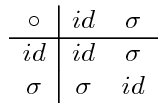
- $\mathfrak S_4$:


