Lösung für Aufgabe 5.3.14
Sei
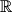
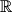 [
[ ]:=
]:=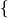 a+b
a+b
 a
a b
b
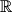
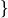
\begin{align*}
(a+b\eps)\oplus(a'+b'\eps) &:= (a+a')+(b+b')\eps, \\
(a+b\eps)\odot(a'+b'\eps) &:= aa'+(ab'+a'b)\eps.
\end{align*}
Weisen Sie nach, dass (\R[\eps],\oplus,\odot) ein Ring ist.
Die Addition ist komponentenweise definiert. Weil (\R,+) eine abelsche Gruppe ist, ist auch (\R[\eps],+) eine abelsche Gruppe.
- Assoziativgesetz: Es gilt
\begin{eqnarray*} ((a+b\eps)\odot(a'+b'\eps))\odot(a''+b''\eps) &=& (aa'+(ab'+a'b)\eps)\odot(a''+b''\eps) = aa'a''+(aa'b''+a''(ab'+a'b))\eps \\ &=& aa'a''+(aa'b''+aa''b'+a'a''b)\eps \\ &=& aa'a''+(a(a'b''+a''b')+a'a''b)\eps = (a+b\eps)\odot(a'a''+(a'b''+a''b')\eps) \\ &=&(a+b\eps)\odot((a'+b'\eps)\odot(a''+b''\eps)). \end{eqnarray*}
- Kommutativgesetz: Es gilt
(a+b\eps)\odot(a'+b'\eps) = aa'+(ab'+a'b)\eps = (a'+b'\eps)\odot(a+b\eps).
- Einselement: (1,0) ist das Einselement:
(a+b\eps)(1+0\eps)=1a+(0a+1b)\eps.
- Distributivgesetz: Es gilt
\begin{eqnarray*} ((a+b\eps)\oplus(a'+b'\eps))\odot(a''+b''\eps) &=& (a+a'+(b+b')\eps)\odot(a''+b''\eps) = (a+a')a''+((a+a')b''+a''(b+b'))\eps \\ &=& aa''+a'a''+(ab''+a'b''+a''b+a''b')\eps = (aa''+(ab''+a''b)\eps)\oplus(a'a''+(a'b''+a''b')\eps) \\ &=&(a+b\eps)\odot(a''+b''\eps)\oplus(a+b\eps)\odot(a''+b''\eps). \end{eqnarray*}
