Wenn Sie das Buch noch nicht kennen, dann können Sie
hier
weitere Informationen finden.
Lösung für Aufgabe 7.2.61
Über einen kreisförmigen Teich mit $12m$ Durchmesser soll ein
$80cm$ breiter Steg gebaut werden. Der Normalabstand der Mittellinie
des Steges vom Mittelpunkt des Teiches soll $6m$ betragen. Die
Stützen des Steges, die genauso breit wie der Steg sind, sollen
außerhalb des Wassers mit $50cm$ Mindestabstand vom Ufer stehen.
Wie weit sind die Stützen voneinander entfernt?
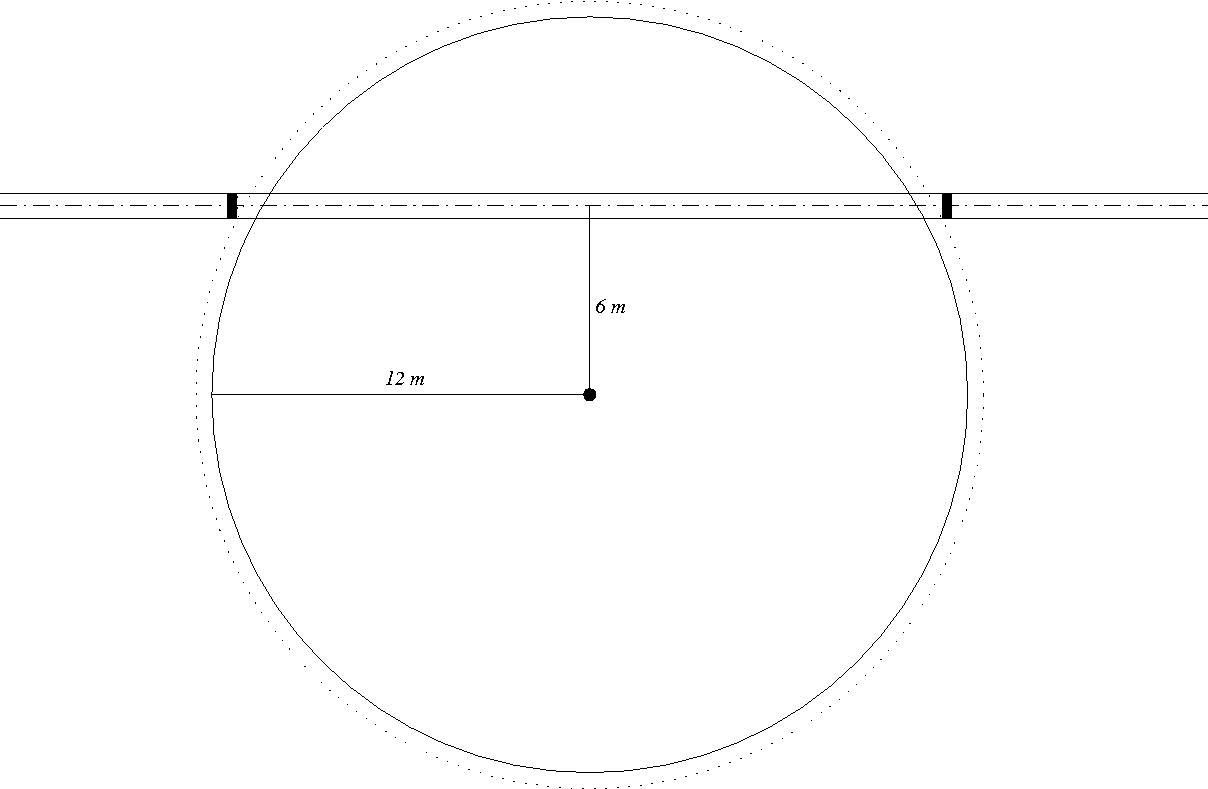
Wir legen den Teich in den Mittelpunkt und betrachten den Kreis, der
die $50\,cm$ Abstand zur Uferlinie sicherstellt: $k:x^2+y^2=(12.5)^2=156.25$.
Die Mittellinie des Steges sei die Gerade $y=6$, und die obere und untere
Begrenzungslinie sind $y=6.4$ und $y=5.6$. Die Stützen sind dem Teich
an der unteren Begrenzungslinie am nächsten, also schneiden wir die
untere Begrenzungslinie mit $k$ und erhalten $x=\pm\frac{\sqrt{12489}}{10}$.
Die Stützen müssen also mindestens
$\frac{\sqrt{12489}}{5}m=22.35\,m$ von einander entfernt sein.
