Next: 4.2.4 Rotations and Euclidean Up: 4.2 Transformations Previous: 4.2.2 Scaling
Now we want to describe the reflection ![]() on a plane orthogonal to some (unit) vector
on a plane orthogonal to some (unit) vector ![]() .
Since any vector
.
Since any vector ![]() can be written as
can be written as
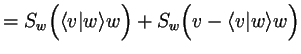 |
||
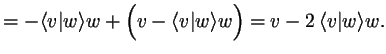 |
In coordinates:
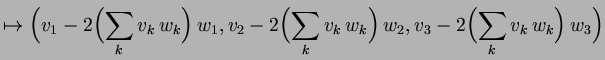 |
||
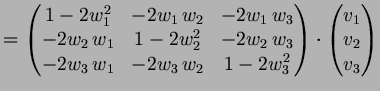 |
||
These reflections are length preserving:
The composition of the two 2-dimensional reflections
![]() and
and
![]() amounts to mirroring
amounts to mirroring
![]() at the center
at the center ![]() .
The composition of two general reflections is a rotation:
.
The composition of two general reflections is a rotation:
Andreas Kriegl 2003-07-23