4.2.6 General Transformations

Beside euclidean motions, conformal linear mappings we have discussed also scaling, where we shrink or stretch the coordinates according to some factors. Scaling can be described by diagonal matrices with the proportionality factors as eigenvalues.

Another kind of mapping of interest is shearing:

$$\begin{pmatrix} 1 & 0 & a \\ 0 & 1 & b \\ 0 & 0 & 1 \end{pmatrix}$$

This is volume preserving, since its determinant is $1$.

We would like to have a common formula for all these transformations. For this we embed $\protect\mathbb{R}^3$ into $\protect\mathbb{R}^4$ via $\langle a,b,c\rangle \mapsto \langle a,b,c,1\rangle$. Then a translation by the vector $v=(v_1,v_2,v_3)$ can be written as

$$\begin{pmatrix} a\\ b \\ c \\ 1 \end{pmatrix}\mapsto \begin{pmatr... ...& 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} a \\ b \\ c \\ 1 \end{pmatrix}$$

Any of the other transformations given by $3\times 3$-matrices can be extended to $4\times 4$-matrices via

$$\begin{pmatrix}a_{1,1} & a_{1,2} & a_{1,3} & 0 \\ a_{2,1} & a_{2... ..._{2,3} & 0 \\ a_{3,1} & a_{3,2} & a_{3,3} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

So all compositions are of the same form

$$\begin{pmatrix}a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4}=v_1 \\ a_{2... ... \\ a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4}=v_3 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

This is written in Pov-Ray as:

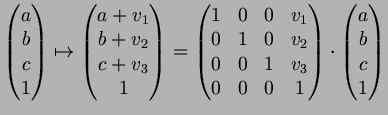
	matrix a11, a21, a31,  
	       a12, a22, a32,  
	       a13, a23, a33,  
	       a14, a24, a34

Note that this is transposed relative to the mathematical version.

An advantage of this description is to be able to describe perspective (no-linear) projections in the same way, see (4.3.2).

Proof. $(4\Rightarrow 5)$ is trivial.

$(5\Rightarrow 6)$ Because of $\Bild P\ni Ph\perp h-Ph\in \Ker P$ we have $\Vert h\Vert^2=\Vert Ph\Vert^2+\Vert h-Ph\Vert^2$ and thus $\Vert Ph\Vert\leq \Vert h\Vert$.

$(4\Leftarrow 6)$ We have $h-Ph=(1-P)h\in\Bild (1-P)=\Ker P$. For $h\perp \Ker P$ we get $0=\langle h-Ph,h \rangle=\Vert h\Vert^2-\langle Ph,h \rangle$, and hence $\Vert h\Vert^2=\langle Ph,h \rangle\leq \Vert Ph\Vert\,\Vert h\Vert\leq \Vert h\Vert^2$. Furthermore $\Vert Ph\Vert=\Vert h\Vert=\sqrt{\langle Ph,h \rangle}$ and $\Vert h-Ph\Vert^2=\Vert h\Vert^2-2\Re(\langle Ph,h \rangle)+\Vert Ph\Vert^2 = 0$ for those $h$. I.e. $(\Ker P)^\perp\subseteq \Ker (1-P)=\Bild P$.
Conversely, let $h\in \Bild P$. Then $h=h_0+h_1$ with $h_0\in\Ker P$ and $h_1\in(\Ker P)^\perp\subseteq \Bild P$. Thus $h_0=h-h_1\in \Bild P\cap\Ker P=\{0\}$, i.e. $h_0=0$ and $h=h_1\in(\Ker P)^\perp$. By orthogonalization we get the desired equation.

$(4\Rightarrow 7)$ Since $v=Pv+(1-P)v$ and $w=Pw+(1-P)w$ with $Pv,Pw\in\Bild P$ and $(1-P)v,(1-P)w\in\Ker P=(\Bild P)^\perp$ we have

$$\langle v,P^*w\rangle = \langle Pv,w\rangle = \langle Pv,Pw+(1-P)w\rangle =\langle Pv,Pw\rangle+0$$

$$= \langle Pv+(1-P)v,Pw\rangle =\langle v,Pw \rangle$$

hence $P=P^*$.

$(4\Leftarrow 7)$ since $\Ker P =\Ker P^*=(\Bild P)^\perp$. $\qedsymbol$

One can even project on some plane orthogonal to $w$ but with rays parallel to some other vector $w'$.

ARRAY(0x8dab5ac)