Next: 4.2.6 General Transformations Up: 4.2 Transformations Previous: 4.2.4 Rotations and Euclidean
The euclidean motions we have just described as
![]() , where
, where ![]() is a rotation or reflection and
is a rotation or reflection and ![]() is a translation vector,
are length and angle preserving.
Now we try to identify those mappings which are only angle preserving.
is a translation vector,
are length and angle preserving.
Now we try to identify those mappings which are only angle preserving.
Lemma (Linear conformal mappings).
Let
![]() be linear. Then the following statements are equivalent:
be linear. Then the following statements are equivalent:
Proof.
![]() let
let ![]() be the angle between
be the angle between ![]() and
and ![]() and
and ![]() the one between
the one between ![]() und
und ![]() .
Then
.
Then
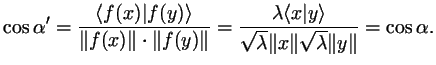
![]() We define
We define
![]() implicitly by
implicitly by
![]() .
.
Let ![]() be orthonormal vectors, then
be orthonormal vectors, then
![]() .
Since
.
Since ![]() is conform, we have:
is conform, we have:
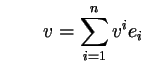 |
||
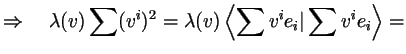 |
||
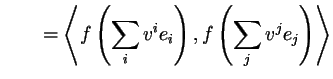 |
||
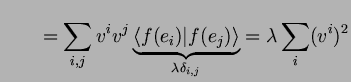 |
||
The lemma now follows from:
Andreas Kriegl 2003-07-23