9 Erzeugenden-Systeme

Um mit bzw. in Vektorräumen rechnen zu können benötigen wir eine Beschreibung ihrer Elemente, der Vektoren, durch Zahlen(-Tupeln) und dazu notwendigerweise den Begriff des Erzeugenden-Systems oder spezieller der Basis.

9.1 Definition.
Eine Teilmenge $S\subseteq V$ eines Vektorraums $V$ heißt Erzeugenden-System von $V$, falls $\langle S\rangle_{\text{VR}}=V$, d.h. der von $S$ erzeugte Teilvektorraum gerade $V$ ist.

Ein Vektorraum heißt endlich-dimensional, wenn er ein endliches Erzeugenden-System besitzt.

Unter einer Basis versteht man ein minimales Erzeugenden-System, d.h. keine echte Teilmenge davon ist noch ein Erzeugenden-System.

9.2 Bemerkung.
Falls ein (endliches) Erzeugenden-System $\{v_1,\dots,v_n\}$ linear-abhängig ist, d.h. 0 als Linearkombination $0=\sum_i \lambda _i v_i$ geschrieben werden kann, wobei $\lambda _i\ne 0$ für mindestens ein $i$ ist (also sich 0 auf einem nicht trivialen Weg im Sinne von (8.16) mit den Richtungen $v_i$ erreichen läßt), so ist das Erzeugenden-System keine Basis, denn es kann ein Vektor $v_i$ (mit $\lambda _i\ne 0$) entfernt werden um ein kleineres Erzeugenden-System zu erhalten: In der Tat ist dann $v_i=-\frac1{\lambda _i}\sum_{j\ne i}\lambda _j\,v_j= \sum_{... ...da _i}{\lambda _j}\,v_j \in \langle S\setminus\{v_i\}\rangle_{\text{VR}}$ und somit $V=\langle S\rangle_{\text{VR}}=\langle \langle S\setminus \... ...ngle_{\text{VR}}=\langle S\setminus\{v_i\}\rangle_{\text{VR}}\subseteq V$.

Lemma.
Ein (endliches) Erzeugenden-System $S=\{v_1,\dots,v_n\}$ ist genau dann eine Basis, wenn aus $\sum_{i=1}^n \lambda _i\, v_i=0$ folgt, daß alle $\lambda _i=0$ sind, d.h. $S$ nicht linear abhängig (also kurz gesagt linear unabhängig) ist.

Beweis. ( $\Rightarrow$) Angenommen $S$ ist nicht linear unabhängig, also linear abhängig, dann existiert nach dem eben Gesagten ein $i$, s.d. $S\setminus\{v_i\}$ ein kleineres Erzeugenden-System ist, ein Widerspruch.

( $\Leftarrow$) Angenommen es wäre $S$ keine Basis, also gäbe es ein echt kleineres Erzeugenden-System $S'$. Sei $v_i\in S\setminus S'$, dann muß $v_i$ eine Linearkombination $\sum_j \lambda _j\,v_j$ der Vektoren $v_j\in S'$ sein und somit $0=v_i-\sum_j \lambda _j\,v_j$ eine Linearkombination von Vektoren aus $S$ mit Koeffizient $\lambda _i=1\ne 0$, ein Widerspruch.     []

9.8 Lemma.
Es sei $B$ ein endliches Erzeugenden-System. Dann existiert eine Basis $B'\subseteq B$.

Beweis. Falls $B$ linear unabhängig ist, so sind wir fertig, denn $B'=B$ ist dann eine Basis wegen dem Lemma in (9.2).

Andernfalls existiert eine Linearkombination $0=\sum_{b\in B}\lambda _b\,b$ und $\lambda _b\ne 0$ für mindestens ein $b\in B$. Dieses $b$ ist dann also eine Linearkombination der übrigen Elemente in $B\setminus\{b\}$, also haben wir ein kleineres Erzeugenden-System gefunden, siehe (9.2). Da $B$ endlich ist erhalten wir nach höchstens $\vert B\vert$ vielen Schritten ein minimales Erzeugenden-System $B'$, also eine Basis.     []

9.9 Folgerung.
Jeder (endlich dimensionale) Vektorraum besitzt eine Basis.

Beweis. Sei $B$ ein endliches Erzeugenden-System. Nach (9.8) existiert dann einen Basis $B'\subseteq B$.     []

Im unendlich dimensionalen Fall ist das viel aufwendiger zu beweisen und erfordert das Auswahlaxiom in einer äquivalenten Formulierung, dem Zorn'schen Lemma, siehe (9.14).

9.3 Lemma.
Eine Menge $\{v_1,\dots,v_n\}$ ist genau dann linear unabhängig, wenn jedes $v\in\langle \{v_1,\dots,v_n\}\rangle_{VR}$ eine eindeutige Darstellung als $v=\sum_{k=1}^n \lambda _k\,v_k$ besitzt.

Beweis. ( $\Rightarrow$) Angenommen $\sum_i \lambda _i\,v_i=v=\sum_i \mu_i\,v_i$ wären zwei Darstellungen von $v$, dann ist $\sum_i(\lambda _i-\mu_i)\,v_i=0$ und da $\{v_1,\dots,v_n\}$ linear unabhängig ist, sind alle Koeffizienten $\lambda _i-\mu_i=0$, also die Darstellung eindeutig.

( $\Leftarrow$) Es sei $0=\sum_{i=1}^n\lambda _i\,v_i$. Da andererseits $0=\sum_{i=1}^n 0\,v_i$ gilt, folgt aus der Eindeutigkeit der Darstellung $\lambda _i=0$ für alle $i$, d.h. $\{v_1,\dots,v_n\}$ ist linear unabhängig.     []

9.4 Beispiel.
Die Einheitsvektoren $e_0:=(1,0,0,\dots,0,0)$, $e_1:=(0,1,0,\dots,0,0)$,..., $e_{n-1}:=(0,0,0,\dots,0,1)$ bilden eine Basis von $\mathbb{K}^n$ die sogenannte Standard-Basis. Jeder Vektor $x=(x_0,\dots,x_{n-1})$ ist offensichtlich folgende Linearkombination der $e_i$, wobei wir die Vektoren der Übersicht halber besser als Spaltenvektoren schreiben:

$$x=\begin{pmatrix}x_0 \\ x_1 \\ x_2 \\ \vdots \... ... \\ 0 \\ 0 \\ \vdots \\ 0 \\ 1\end{pmatrix}= \sum_{i=0}^{n-1} x_i\,e_i,$$

also ist $\{e_1,\dots,e_n\}$ ein Erzeugenden-System.

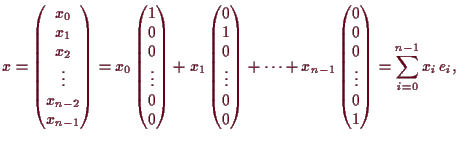
Dieses ist linear unabhängig, denn aus $0=\sum_i\lambda _i\,e_i$ folgt

$$\begin{pmatrix}0 \\ 0 \\ 0 \\ \vdots \\ 0 \\ 0... ...rix}\lambda _1 \\ \lambda _2 \\ \\ \vdots \\ \\ \lambda _n \end{pmatrix}$$

also sind alle $\lambda _i=0$.

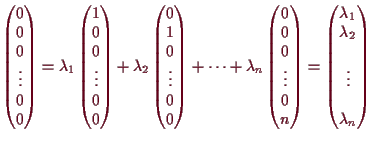
9.5 Beispiel.
Eine Ebene sei durch

$$E:=\Bigl\{(x_1,x_2,x_3)\in\mathbb{R}^3:\sum_{i=1}^3 a_i\,x_i=0\Bigr\}$$

mit $(a_1,a_2,a_3)\ne 0$ gegeben. O.B.d.A. sei $a_3\ne 0$. Dann bilden z.B.  $v_1:=(-a_3,0,a_1)$ und $v_2:=(0,-a_3,a_2)$ eine Basis der Ebene: Offensichtlich gilt $v_1,v_2\in E$. Weiters sei $(x_1,x_2,x_3)\in E$, dann gibt es eine eindeutig bestimmte Zahlen $\lambda _1$ und $\lambda _2$ mit

$$\begin{pmatrix}x_1 \\ x_2\\ x_3 \end{pmatrix}=... ..._3 \\ -\lambda _2\,a_3 \\ \lambda _1\,a_1+\lambda _2\,a_2 \end{pmatrix}$$

nämlich $\lambda _1:=-\frac{x_1}{a_3}$, $\lambda _2=-\frac{x_2}{a_3}$ und somit $\lambda _1\,a_1+\lambda _2\,a_3=-\frac{a_1\,x_1+a_2\,x_2}{a_3}=-\frac{-a_3\,x_3}{a_3}=x_3$. In der Schule ist dies gerade die Methode eine Parameterdarstellung einer durch Gleichung beschriebenen Ebene (durch 0) zu finden indem man zwei Richtungsvektoren $v_1$ und $v_2$ angibt.

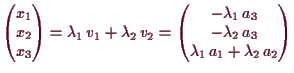
9.6 Beispiel.
Die Monome $e_i:x\mapsto x^i$ für $i\in\mathbb{N}$ bilden ein (unendliches) Erzeugenden-System der Polynome $\mathbb{K}[x]$ und damit auch der polynomialen Funktionen: In der Tat ist jedes Polynom $p\in\mathbb{K}[x]$ nach Definition eine endliche Summe der Form $p=\sum_i p_i\,e_i$ mit Koeffizienten $p_i\in\mathbb{K}$, denn

$$p(x)=\sum_i p_i\,x^i=\sum_i p_i\, e_i(x)=\Bigl(\sum_i p_i\, e_i\Bigr)(x)$$

Für $\mathbb{K}\in\{\mathbb{R},\mathbb{C},\mathbb{Q}\}$ bilden diese sogar eine Basis, denn aus $\sum_i \lambda _i\,e_i=0$ in $K[x]$ folgt $p(x):=\sum_i \lambda _i\, x^i=0$ für alle $x\in \mathbb{K}$ und da ein Polynom $p\ne 0$ nur soviele Nullstellen haben kann, wie sein Grad ist, folgt, falls $\mathbb{K}$ unendlich ist, daß $p$ das Nullpolynom ist, also alle Koeffizienten $\lambda _i=0$ sind.

Für $\mathbb{K}=\mathbb{Z}_2$ ist hingegen schon $\{e_0,e_1\}$ eine Basis der polynomialen Funktionen, denn $x^n=x$ für alle $x\in\mathbb{Z}_2$ und $n\geq 1$.

9.7 Beispiel.
Es ist $\mathbb{R}[x]$ unendlich-dimensional, denn gäbe es ein (anderes) endliches Erzeugenden-System $\{p_1,\dots,p_n\}$, dann kann dieses nur Polynome vom Grad höchstens $d:=\max\{\operatorname{grad}(p_1),\dots,\operatorname{grad}(p_n)\}$ erzeugen und das Monom $e_{d+1}$ z.B. hat aber größeren Grad.

Für unendliches $X$ ist auch $\mathbb{R}^X$ unendlich-dimensional:
Wäre nämlich $\{f_1,\dots,f_n\}$ eine Erzeugenden-System, so wählen wir paarweise verschiedene $x_k\in X$ und eine Funktion $f:X\to\mathbb{R}$ mit $f(x_k)>k\,\sum_{i=1}^n\vert f_i(x_k)\vert$ für alle $k\in\mathbb{N}$, die nun keine Linearkombination der $f_k$ seien kann, denn aus

$$f=\sum_i \lambda _i\, f_i$$

folgt für $x_k$ mit $k>\vert\lambda _i\vert$ für alle $i\leq n$

$$\sum_i \lambda _i\, f_i(x_k)=f(x_k)>k\,\sum_{i... ..._i(x_k)\vert\geq \Bigl\vert\sum_{i=1}^n \lambda _i\,f_i(x_k)\Bigr\vert,$$

ein Widerspruch.

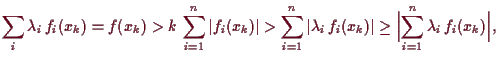
9.10 Definition.
Unter der Dimension (man schreibt $\dim(V)$) eines (endlich-dimensionalen) Vektorraums $V$ versteht man die minimale Kardinalität (Anzahl) eines Erzeugenden-Systems.

Es gibt also mindestens eine Basis von $V$ mit $\dim(V)$ vielen Elementen. Wir wollen nun zeigen, daß dies für alle Basen der Fall ist.

9.11 Austauschlemma.
Sei $V$ ein Vektorraum über einem Körper $\mathbb{K}$, $A\subseteq V$ eine beliebige Teilmenge, und $v=\sum_{a\in A}\lambda _a a\in \langle A\rangle$ ein beliebiges Element. Sei $a_0\in A$ so, daß $\lambda _{a_0}\neq 0$ gilt, und sei $A'=(A\setminus\{a_0\})\cup\{v\}$. Dann gilt $\langle A'\rangle=\langle A\rangle$. (Man kann also $a_0\in A$ durch $v$ ersetzen, ohne das Erzeugnis zu verändern.)

Beweis. Nach Voraussetzung ist $v\in\langle A\rangle$, also $A'\subseteq \langle A\rangle$, und damit $\langle A'\rangle\subseteq \langle A\rangle$ nach Definition (8.15). Andererseits ist $v=\lambda _{a_0}a_0+\sum_{a\in A\setminus\{a_0\}}\lambda _aa$ mit $\lambda _{a_0}\neq 0$. Damit erhalten wir aber $a_0=\lambda _{a_0}^{-1}v+\sum_{a\in A\setminus\{a_0\}}(-\lambda _{a_0}^{-1}\lambda _a)a$, und das ist eine Linearkombination von Vektoren aus $A'$. Somit ist $a_0\in\langle A'\rangle$ und damit $A\subseteq \langle A'\rangle$, was wiederum nach Definition (8.15) $\langle A\rangle\subseteq \langle A'\rangle$ liefert.     []

9.12 Austauschsatz von Steinitz.
Sei $V$ ein Vektorraum und $W$ ein endliches Erzeugenden-System. Ist $A\subseteq V$ linear unabhängig, dann existiert eine injektive Abbildung $f:A\to W$ s.d. $A\cup (W\setminus f(A))$ ein Erzeugenden-System ist. Insbesonders ist $\vert A\vert\leq \vert W\vert$.

Beweis. Wir machen Induktion nach $\vert A\vert$: Falls $A=\emptyset$ ist, so ist nichts zu zeigen. Sei nun $A'=A\cup\{a'\}$ mit $a'\notin A$. Nach Induktionsannahme existiert ein injektives $f:A\to W$ mit $A\cup (W\setminus f(A))$ erzeugend. Also ist $a'=\sum_{a\in A} \lambda _a\,a+\sum_{w\in W\setminus f(A)}\lambda _w\,w$. Da $A'$ linear unabhängig ist, muß wegen $0\ne a'-\sum_{a\in A}\lambda _a\,a=\sum_{w\in W\setminus f(A)}\lambda _w\,w$ der Koeffizient $\lambda _w\ne 0$ für mindestens ein $w$ sein. Wir wählen so ein $w$ und nennen es $w'$ und definieren $f':A'\to W$ durch $f'\vert _A=f$ und $f(a'):=w'$. Dann ist $f'$ injektiv, da $f$ injektiv ist und $w'\in W\setminus f(A)$. Nach dem Austauschlemma ist $A'\cup (W\setminus f'(A'))=((A\cup (W\setminus f(A)))\setminus \{w'\})\cup\{a'\}$ ein Erzeugenden-System.

Es ist $\vert A\vert\leq \vert W\vert$, denn $f(A)\subseteq W$ und somit $\vert W\vert\geq \vert f(A)\vert=\vert A\vert$.     []

9.13 Folgerung.
Es sei $V$ ein endlich dimensionaler Vektorraum. Dann gilt:

1.

Je zwei Basen haben gleich viele Elemente. Diese Anzahl heißt Dimension des Vektorraums.

2.

Jede linear unabhängige Menge kann zu einer Basis erweitert werden.

3.

Jedes Erzeugenden-System kann zu einer Basis verkleinert werden.

4.

Jede linear unabhängige Menge $B$ erfüllt $\vert B\vert\leq \dim(V)$.

5.

Jedes Erzeugenden-System $B$ erfüllt $\vert B\vert\geq \dim(V)$.

6.

Ist $B\subseteq V$ mit $\vert B\vert=\dim(V)$ ein Erzeugenden-System oder linear unabhängig, so ist es eine Basis.

Basen sind also nach (2) und (3) minimale Erzeugenden-Systeme oder äquivalent maximale linear unabhängige Teilmengen.

Beweis. (1). Seien $B$ und $B'$ zwei Basen mit $\vert B\vert<{\infty}$. Da $B'$ linear unabhängig ist und $B$ ein Erzeugenden-System ist, ist $\vert B'\vert\leq \vert B\vert$ nach (10.7). Da $B'$ somit ein endliches erzeugenden-System und $B'$ linear unabhängig ist, ist andererseits $\vert B\vert\leq\vert B'\vert$, also gilt Gleichheit.

(2). Sei $B$ eine endliche Basis und $A$ linear unabhängig. Nach (10.7) existiert eine injektive Abbildung $f:A\to B$, s.d. die Obermenge $A':=A\cup (B\setminus f(A))\supseteq A$ ein Erzeugenden-System ist. Um nun auch lineare Unabhängigkeit von $A'$ zu erreichen wählen wir ein minimales $B'\subseteq B\setminus f(A)$, s.d. $A\cup B'$ ein Erzeugenden-System ist. So ein minimales $B'$ existiert da $B$ endlich ist. Es ist $A\cup B'\supseteq A$ auch linear unabhängig und somit eine Basis, denn andernfalls wäre $0=\sum_{a\in A}\lambda _a\,a+\sum_{b'\in B}\lambda _{b'}\,b'$ und nicht alle $\lambda$ gleich 0. Da aber $A$ linear unabhängig ist, muß $\lambda _{b'}\ne 0$ sein für mindestens ein $b'\in B$ und folglich wäre $A\cup (B'\setminus\{b'\})$ ein kleineres Erzeugenden-System.

(3). Sei $A$ ein Erzeugenden-System. Mittels Induktion nach $\vert A'\vert$ konstruieren wir linear unabhängige Teilmengen $A'\subseteq A$. Für $\vert A'\vert=0$ sei $A'=\emptyset$. Falls $A'$ erzeugend (d.h. eine Basis) ist, so sind wir fertig. Nach (10.7) existiert ein injektives $f:A'\to W$ mit $A'\cup (W\setminus f(A'))$ erzeugend. Also ist $A'$ spätestens dann erzeugend, wenn $\vert A'\vert=\vert W\vert$ .

Andernfalls wähle $a\in A\setminus \langle A'\rangle$ (andernfalls ist $V=\langle A\rangle= \langle A'\rangle$). Dann ist $A'\cup \{a\}$ linear unabhängig, denn $A'$ ist es und $a\notin\langle A'\rangle$.

(4). Sei $B$ linear unabhängig und $B'\supseteq B$ eine Basis nach (2). Dann ist $\vert B\vert\leq \vert B'\vert=\dim(V)$.

(5). Sei $B$ erzeugend und $B'\subseteq B$ eine Basis nach (3). Dann ist $\vert B\vert\geq \vert B'\vert=\dim(V)$.

(6). $B$ ist maximale linear unabhängige Teilmenge (resp. minimales Erzeugenden-System) nach (4) (resp. (5)). Also eine Basis nach (2) und (3).     []

Für Basen in ${\infty}$-dimensionalen Vektorräumen benötigen wir Ordinalzahlen. Diese sind eine Verallgemeinerung der natürlichen Zahlen, welche wir rekursiv als $n^+:=n\cup\{n\}=\{0,1,2,\dots,n\}$ definiert haben. Für natürliche Zahlen $n,m$ ist $n<m$ $\Leftrightarrow$ $n\in m$. Die Menge $\mathbb{N}$ aller natürlichen Zahlen ist wohlgeordnet. Allgemein heißt nun eine Menge Ordinalzahl, wenn sie bezüglich der $\in$-Relation wohlgeordnet ist. Insbesonders ist jede natürliche Zahl aber auch $\mathbb{N}$ eine Ordinalzahl. Letztere wird auch gerne mit $\omega$ bezeichnet. Man zeigt leicht, daß für jede Ordinalzahl $\alpha$ auch $\alpha ^+:=\alpha \cup\{\alpha \}$ eine Ordinalzahl ist. Somit sind auch $\omega +1$, $\omega +2$, ...Ordinalzahlen. Ebenso deren Vereinigung $2\omega :=\omega +\omega :=\bigcup_{n\in\mathbb{N}}\omega +n$. Und folglich auch $2\omega +1$, $2\omega +2$, ...und analog $3\omega :=2\omega +\omega$, $4\omega$, ..., sowie deren Vereinigung $\bigcup_{n\in\mathbb{N}}n\omega =\omega \omega =:\omega ^2$, und analog $\omega ^3$, $\omega ^4$,..., sowie deren Vereinigung $\omega ^\omega$, u.s.w..

Man kann zeigen, daß die Ordinalzahlen bzgl. $\in$ wohlgeordnet sind. Somit existiert für jede Menge von Ordinalzahlen das Minimum, man kann Ordnungsinduktion (man sagt auch transfinite Induktion dazu) für Ordinalzahlen machen und Funktionen auf den Ordinalzahlen rekursive (man sagt auch durch transfinite Rekursion) definieren. Da man mittels Auswahlaxiom zeigen kann, daß jede Menge gleichmächtig zu einer Ordinalzahl ist, ist transfinite Induktion eine Möglichkeit etwas für alle Mengen zu zeigen.

Diese Hilfsmittel verwenden wir nun in der folgenden Proposition.

9.14 Zorn'sche Lemma.
Sei $(X,\preceq)$ eine partiell geordnete Menge, sodaß jede lineare geordnete Teilmenge eine obere Schranke besitzt. Dann existieren maximale Elemente in $(X,\preceq)$.

Beweis. Es sei $(X,\preceq)$ eine partiell geordnete Menge, die die Voraussetzungen des Zorn'schen Lemmas erfüllt. Wegen dem Auswahlaxiom existiert eine Abbildung

$$F:\mathcal{P}(X)\setminus \{\emptyset\}\to X=\bigcup (\mathcal{P}(X)\setminus \{\emptyset\})$$

mit $F(A)\in A$ für alle $\emptyset\ne A\subseteq X$. Es sei ein fixes $\gamma \notin X$ gewählt. Mittels transfiniter Rekursion definieren wir für jede Ordinalzahl $\alpha$ ein $y_\alpha \in X\cup\{\gamma \}$ durch

$$y_\alpha := \begin{cases}F(A_\alpha ) &\text{f... ..._\beta \prec x\}\ne\emptyset \\ \gamma &\text{andernfalls}. \end{cases}$$

Die Zuordnung $\alpha \mapsto y_\alpha$ ist streng monoton auf $\{\alpha :y_\alpha \ne\gamma \}$, denn sei $\beta <\alpha$ und $y_\alpha \ne\gamma$, also $A_\alpha \ne\emptyset$ und somit $y_\alpha =F(A_\alpha )\in A_\alpha$, d.h. $y_\beta \prec y_\alpha$ für $\beta <\alpha$.

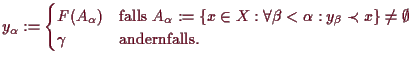
Da es mehr als eine Menge Ordinalzahlen gibt, $X$ nur eine Menge ist und $\alpha \mapsto y_\alpha$ injektiv auf $\{\alpha :y_\alpha \ne\gamma \}$ ist, existiert eine Ordinalzahl $\alpha$ mit $y_\alpha =\gamma$. Da die Ordinalzahlen wohlgeordnet sind existiert eine kleinste solche Ordinalzahl und wir nennen sie $\alpha _0$. Die Menge $\{y_\alpha :\alpha <\alpha _0\}$ ist somit eine linear geordnete Teilmenge von $(X,\preceq)$ und besitzt nach Voraussetzung eine obere Schranke $x_0$. Wir zeigen nun, daß $x_0$ ein maximales Element ist. Andernfalls existiert ein $x_1\in X$ mit $x_0\prec x_1$. Da $y_\alpha \preceq x_0\prec x_1$ alle $\alpha <\alpha _0$ ist dann $A_{\alpha _0}\ne\emptyset$ und somit $y_{\alpha _0}\ne \gamma$, ein Widerspruch.     []

9.15 Folgerung.
Jeder Vektorraum besitzt eine Basis.

Beweis. Wir zeigen mehr noch: Sei $V$ ein Vektorraum über einem Körper $\mathbb{K}$, $A\subseteq V$ eine linear unabhängige Teilmenge und $E\subseteq V$ ein Erzeugenden-System mit $A\subseteq E$. Dann gibt es eine Basis $B$ von $V$ mit $A\subseteq B\subseteq E$.
Wie betrachten die Menge $\mathcal{B}$ aller linear unabhängigen Teilmengen $C\subseteq V$, die $A\subseteq C\subseteq E$ erfüllen. Wir definieren eine Halbordnung auf dieser Menge durch $C\leq C'$ genau dann, wenn $C\subseteq C'$. Sei $\mathcal{A}\subseteq \mathcal{B}$ eine Teilmenge, auf der dies eine Totalordnung ist und betrachte $X:=\bigcup_{C\in\mathcal{A}}C$. Sind $x_1,\dots,x_n\in X$ und $\lambda _1,\dots,\lambda _n\in\mathbb{K}$ endlich viele Elemente sodaß $\lambda _1x_1+\dots+\lambda _nx_n=0$ gilt, dann gibt es $C_1,\dots,C_n\in\mathcal{A}$, sodaß $x_i\in C_i$ für jedes $i$. Da $\mathcal{A}$ durch die Inklusion total geordnet ist, gilt für $i,j=1,\dots,n$ entweder $C_i\subseteq C_j$ oder $C_j\subseteq C_i$. Daraus folgt aber leicht, daß es ein $i_0$ gibt, sodaß $C_i\subseteq C_{i_0}$ für alle $i$ gilt. Da die Menge $C_{i_0}$ in $\mathcal{A}\subseteq \mathcal{B}$ liegt ist sie linear unabhängig, also folgt $\lambda _i=0$ für alle $i$. Somit ist $X$ linear unabhängig. Offensichtlich gilt $A\subseteq X\subseteq E$, weil das für jedes $C\in\mathcal{A}$ gilt, also ist $X\in\mathcal{B}$ eine obere Schranke für $A$.

Nach dem Zorn'schen Lemma (9.14) erhalten wir ein maximales Element $B_0\in\mathcal{B}$. Damit ist $A\subseteq B_0\subseteq E$ und $B_0$ linear unabhängig. Da $B_0$ maximal ist, ist für jedes Element $y\in E\setminus B_0$ die Menge $B_0\cup\{y\}$ linear abhängig, und man sieht leicht, daß dies nur möglich ist, wenn $y\in\langle B_0\rangle$ gilt. Damit folgt aber $E\subseteq \langle B_0\rangle$, und weil $E$ ein Erzeugenden-System ist, ist auch $B_0$ ein Erzeugenden-System, also eine Basis.     []

9.16 Folgerung.
Jeder Teilraum $W$ eines Vektorraums $V$ besitzt einen Komplementärraum $W'$. Insbesonders ist $\dim(V)=\dim(W)+\dim(W')$.

Beweis. Sei $B$ eine Basis von $W$. Dann ist $B$ linear unabhängig in $V$ und somit existiert eine Menge $B'$, s.d. $B\cup B'$ eine Basis von $V$ ist. Nun sieht man leicht, daß der von $B'$ erzeugte Teilvektorraum $W'$ ein Komplementärraum zu $W$ ist.     []

9.17 Folgerung.
Für Teilräume $V_1,V_2\leq V$ gilt: $\dim(V_1+V_2)=\dim(V_1)+\dim(V_2)-\dim(V_1\cap V_2)$.

Beweis. Wir wählen Komplemente $W_i$ zu $V_1\cap V_2$ in $V_i$. Dann ist $V_1+V_2=W_1\oplus (V_1\cap V_2)\oplus W_2$ und $\dim(W_i)+\dim(V_1\cap V_2)=\dim(V_i)$.     []