Nächste Seite: 5 Die rationalen Zahlen Aufwärts: Mathematik 1 für Informatik Vorherige Seite: 3 Die natürlichen Zahlen Inhalt Index
Descartes nannte die negativen ganzen Zahlen auch ``falsche Zahlen''.
4.1 Konstruktion von
![]() .
.
Um auch für natürliche Zahlen
![]() Gleichungen der Form
Gleichungen der Form
![]() zu lösen,
benötigen wir ein Inverses (welches wir mit
zu lösen,
benötigen wir ein Inverses (welches wir mit
![]() bezeichnen)
zu jedem
bezeichnen)
zu jedem
![]() .
Da in jeder Gruppe das neutrale Element
invers zu sich selbst ist, ist
.
Da in jeder Gruppe das neutrale Element
invers zu sich selbst ist, ist
![]() .
Somit sollte die Menge der ganzen Zahlen durch
.
Somit sollte die Menge der ganzen Zahlen durch
![]() gegeben sein.
gegeben sein.
Um die Operationen für
![]() ohne Fallunterscheidungen zu definieren,
betrachten wir für
ohne Fallunterscheidungen zu definieren,
betrachten wir für
![]() ein Symbol
ein Symbol
![]() (die virtuelle Lösung der Gleichung
(die virtuelle Lösung der Gleichung
![]() ).
Die Menge
).
Die Menge
![]() sollte auch als Menge
sollte auch als Menge
![]() aller Lösungen beschrieben werden können.
Wir versuchen nun mit diesen Lösungen
aller Lösungen beschrieben werden können.
Wir versuchen nun mit diesen Lösungen
![]() zu rechnen.
Natürlich erwarten wir, daß
zu rechnen.
Natürlich erwarten wir, daß
![]() durch
durch
![]() gegeben ist, wobei
gegeben ist, wobei
![]() das (zu findende) Inverse von
das (zu findende) Inverse von
![]() ist.
Wegen
ist.
Wegen
![]() sollte
sollte
![]() sein.
Dies sieht man auch wie folgt ein:
sein.
Dies sieht man auch wie folgt ein:
Diese Relation ist mit der Addition verträglich
(man sagt
![]() ist eine Kongruenzrelation),
denn aus
ist eine Kongruenzrelation),
denn aus
![]() und
und
![]() folgt
folgt
![]() da
da
Die Multiplikation auf
![]() erweitert sich ebenfalls zu einer Operation
auf
erweitert sich ebenfalls zu einer Operation
auf
![]() durch
durch
![]() .
Idee dabei ist
.
Idee dabei ist
![]() .
Auch diese Operation ist mit
.
Auch diese Operation ist mit
![]() verträglich, denn
aus
verträglich, denn
aus
![]() , also
, also
![]() , folgt
, folgt
![]() , d.h.
, d.h.
![]() .
Also ist auch
.
Also ist auch
![]() eine kommutative Halbgruppe mit
eine kommutative Halbgruppe mit
![]() .
Weiters gilt das distributiv-Gesetz, d.h.
.
Weiters gilt das distributiv-Gesetz, d.h.
![]() ist ein kommutativer Ring mit
ist ein kommutativer Ring mit
![]() .
.
Allerdings ist
![]() kein Körper
den außer
kein Körper
den außer
![]() hat kein einziges Element
hat kein einziges Element
![]() ein multiplikatives
Inverses.
Trotzdem ist
ein multiplikatives
Inverses.
Trotzdem ist
![]() ein Integritätsbereich, d.h.
es ist ein kommutativer Ring mit 1, der nullteilerfrei ist.
ein Integritätsbereich, d.h.
es ist ein kommutativer Ring mit 1, der nullteilerfrei ist.
4.2
Unendliche Zifferndarstellung negativer ganzer Zahlen.
Wendet man das übliche Verfahren zur Berechnung der Differenz
![]() zweier Zahlen auch im Falle
zweier Zahlen auch im Falle
![]() an so erhält man z.B. für Dezimalzahlen
an so erhält man z.B. für Dezimalzahlen
![]() in der Binärdarstellung:
in der Binärdarstellung:
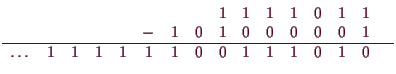
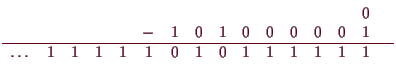
| binär | hexadezimal | unsigned byte | signed byte |
| 00000000 | 00 | 0 | 0 |
| 00000001 | 01 | 1 | 1 |
| &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; |
| 01111110 | 7E | 126 | 126 |
| 01111111 | 7F | 127 | 127 |
| 10000000 | 80 | -128 | 128 |
| 10000000 | 81 | -127 | 129 |
| &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; |
| 11111110 | FE | -2 | 254 |
| 11111111 | FF | -1 | 255 |
4.3 Restklassenringe.
Auch die Restklassenringe
![]() für
für
![]() sind kommutative Ringe
mit 1, wobei
die Addition und Multiplikation von Klassen durch
sind kommutative Ringe
mit 1, wobei
die Addition und Multiplikation von Klassen durch
Insbesonders sind
![]() und
und
![]() Integritätsbereiche (und sogar Körper,
wie wir in (4.7) zeigen werden)
Integritätsbereiche (und sogar Körper,
wie wir in (4.7) zeigen werden)
![]() ,
,
![]() und
und
![]() hingegen nicht einmal Integritätsbereiche.
hingegen nicht einmal Integritätsbereiche.
4.4 Definition.
Es sei
![]() ein Integritätsbereich und
ein Integritätsbereich und
![]() .
Dann heißt
.
Dann heißt
![]() Teiler von
Teiler von
![]() falls
ein
falls
ein
![]() existiert mit
existiert mit
![]() .
Ein größter gemeinsamer Teiler (kurz ggT)
von
.
Ein größter gemeinsamer Teiler (kurz ggT)
von
![]() und
und
![]() ist ein Element
ist ein Element
![]() welches
welches
![]() und
und
![]() teilt, und welches von jedem anderen gemeinsamen Teiler
geteilt wird.
Falls 1 ein größter gemeinsamer Teiler ist, so heißen
teilt, und welches von jedem anderen gemeinsamen Teiler
geteilt wird.
Falls 1 ein größter gemeinsamer Teiler ist, so heißen
![]() und
und
![]() relativ
prim.
relativ
prim.
4.5 Proposition. Charakterisierung des ggT.
Die Menge
![]() der größte gemeinsame Teiler zweier Elemente
der größte gemeinsame Teiler zweier Elemente
![]() und
und
![]() eines Integritätsbereichs erhält man durch Multiplikation eines ggT mit allen
Einheiten (d.h. invertierbaren Elementen).
eines Integritätsbereichs erhält man durch Multiplikation eines ggT mit allen
Einheiten (d.h. invertierbaren Elementen).
In
Beweis. Es sei
Sei nun
![]() ein ggT von
ein ggT von
![]() und
und
![]() und
und
![]() eine Einheit, dann ist
eine Einheit, dann ist
![]() ebenfalls ein ggT von
ebenfalls ein ggT von
![]() und
und
![]() :
Nach obigen ist
:
Nach obigen ist
![]() ein Teiler von
ein Teiler von
![]() und
und
![]() .
Sei
.
Sei
![]() ein weiterer gemeinsamer Teiler von
ein weiterer gemeinsamer Teiler von
![]() und
und
![]() .
Dann ist
.
Dann ist
![]() ein Teiler von
ein Teiler von
![]() . Da
. Da
![]() invertierbar ist, existiert
invertierbar ist, existiert
![]() und ist auch eine Einheit. Somit ist auch
und ist auch eine Einheit. Somit ist auch
![]() ein Teiler
von
ein Teiler
von
![]() , d.h. es existiert ein
, d.h. es existiert ein
![]() mit
mit
![]() , also
, also
![]() , somit ist
, somit ist
![]() auch Teiler von
auch Teiler von
![]() .
.
Sei schließlich
![]() ein weiterer ggT von
ein weiterer ggT von
![]() und
und
![]() . Dann
teilen sich
. Dann
teilen sich
![]() und
und
![]() gegenseitig, also existieren
gegenseitig, also existieren
![]() und
und
![]() mit
mit
![]() und
und
![]() , also
ist
, also
ist
![]() und da wir Nullteilerfreiheit
vorausgesetzt haben (und Teiler nicht 0 sind)
ist
und da wir Nullteilerfreiheit
vorausgesetzt haben (und Teiler nicht 0 sind)
ist
![]() , also
, also
![]() eine Einheit mit
eine Einheit mit
![]() .
'ed
.
'ed
Euklid'ischer Algorithmus.
Man kann den ggT von
![]() wie folgt bestimmen (ohne die aufwendige
Bestimmung der Primfaktorenzerlegung von
wie folgt bestimmen (ohne die aufwendige
Bestimmung der Primfaktorenzerlegung von
![]() und
und
![]() ).
Sei dazu O.B.d.A.
).
Sei dazu O.B.d.A.
![]() .
Wir setzen
.
Wir setzen
![]() und
und
![]() und berechnen mittels Division mit Rest rekursiv
und berechnen mittels Division mit Rest rekursiv
![]() und
und
![]() mit
mit
![]() mit
mit
![]() .
Nach höchstens
.
Nach höchstens
![]() Schritten ist
Schritten ist
![]() . Das letzte
. Das letzte
![]() ist dann ein ggT
ist dann ein ggT
![]() von
von
![]() und
und
![]() .
.
Beweis. Aus der letzten Gleichung der Rekursion folgt, daß
Weiters können wir die Gleichungen rekursiv bei der vorletzten Gleichung beginnend nach oben fortschreitend auflösen und erhalten:
Falls ein
![]() sowohl
sowohl
![]() als auch
als auch
![]() und damit die rechte Seite teilt, so
teilt
und damit die rechte Seite teilt, so
teilt
![]() auch die linke Seite
auch die linke Seite
![]() .
Also ist
.
Also ist
![]() ein ggT von
ein ggT von
![]() und
und
![]() .
[]
.
[]
4.6 Beispiel.
Wir bestimmen mittels Euklid'ischen Algorithmus den ggT von
![]() und
und
![]() :
Fortgesetze Division mit Rest liefert:
:
Fortgesetze Division mit Rest liefert:
4.7 Folgerung.
Eine Restklasse
![]() ist genau dann eine Einheit, wenn
1 ein ggT von
ist genau dann eine Einheit, wenn
1 ein ggT von
![]() und
und
![]() ist, d.h.
ist, d.h.
![]() und
und
![]() relativ prim sind.
relativ prim sind.
Somit ist
![]() genau dann ein Körper, wenn
genau dann ein Körper, wenn
![]() eine Primzahl ist.
eine Primzahl ist.
Beweis. Wegen dem Euklid'ischen Algorithmus ist
Polynome
3.32 Definition.
Unter einem reellen Polynom
![]() verstehen wir eine Funktion
verstehen wir eine Funktion
![]() , welche durch
, welche durch
![]() mit
mit
![]() und
gewissen Koeffizienten
und
gewissen Koeffizienten
![]() gegeben ist.
gegeben ist.
Manchmal ist es günstiger Polynome als formal unendliche Summen
![]() zu schreiben, wobei halt in Wirklichkeit
fast alle Koeffizienten
zu schreiben, wobei halt in Wirklichkeit
fast alle Koeffizienten
![]() gleich 0 sind,
d.h. alle bis auf endlich viele.
gleich 0 sind,
d.h. alle bis auf endlich viele.
Wir können Funktionen
![]() addieren und multiplizieren:
addieren und multiplizieren:
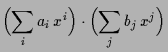 |
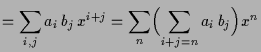 |
|
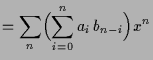 |
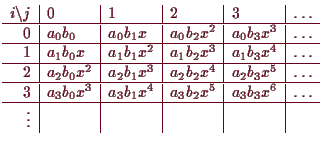
Da reelle Polynome
![]() eindeutig durch ihre Koeffizienten
eindeutig durch ihre Koeffizienten
![]() beschrieben
werden (siehe (4.13a)), können wir diese auch als die Teilmenge
beschrieben
werden (siehe (4.13a)), können wir diese auch als die Teilmenge
Allgemeiner sei nun
![]() ein kommutativer Ring mit 1 und
ein kommutativer Ring mit 1 und
![]() eine Menge.
Dann ist auch die Menge
eine Menge.
Dann ist auch die Menge
![]() aller Abbildungen
aller Abbildungen
![]() ein
kommutativer Ring mit 1 vermöge der Operationen:
ein
kommutativer Ring mit 1 vermöge der Operationen:
Jedes Polynom
![]() können wir natürlich als polynomiale Funktion
können wir natürlich als polynomiale Funktion
![]() vermöge
vermöge
![]() auffassen.
Dies liefert einen Homomorphismus (d.h. Abbildung, die mit Addition und
Multiplikation verträglich ist)
auffassen.
Dies liefert einen Homomorphismus (d.h. Abbildung, die mit Addition und
Multiplikation verträglich ist)
![]() , der aber für
endliche Ringe
, der aber für
endliche Ringe
![]() nicht injektiv zu sein braucht.
Für
nicht injektiv zu sein braucht.
Für
![]() z.B. ist die zum Monom
z.B. ist die zum Monom
![]() gehörende
polynomiale Funktion
gehörende
polynomiale Funktion
![]() für jedes
für jedes
![]() durch die Identität
durch die Identität
![]() gegeben.
gegeben.
Man schreibt statt der Folge
![]() üblicherweise
die ``formale Summe''
üblicherweise
die ``formale Summe''
![]() damit die Formeln für die Addition
und Multiplikation sich durch formale Anwendung des distributiv-Gesetzes
ergeben.
damit die Formeln für die Addition
und Multiplikation sich durch formale Anwendung des distributiv-Gesetzes
ergeben.
Der Grad
![]() eines Polynoms
eines Polynoms
![]() ist der größte Index
ist der größte Index
![]() der nicht verschwindenden Koeffizienten
der nicht verschwindenden Koeffizienten
![]() diese Polynoms,
oder wie man auch sagt der Index des führenden Koeffizienten.
diese Polynoms,
oder wie man auch sagt der Index des führenden Koeffizienten.
Es ist
![]() und
und
![]() falls
falls
![]() ein Integritätsbereich ist.
Für das Nullpolynom ergäbe sich daraus
ein Integritätsbereich ist.
Für das Nullpolynom ergäbe sich daraus
![]() für alle
Polynome
für alle
Polynome
![]() . Diese Gleichung in
. Diese Gleichung in
![]() ist in
ist in
![]() nicht lösbar, aber
nicht lösbar, aber
![]() erfüllt sie, also setzt man
erfüllt sie, also setzt man
![]() .
.
Die Summanden
![]() heißen auch Monome vom Grad
heißen auch Monome vom Grad
![]() .
.
Man schreibt oft
![]() für die Menge der Polynome vom
Grad kleiner oder gleich
für die Menge der Polynome vom
Grad kleiner oder gleich
![]() .
.
4.8 Lemma.
Ein reelles Polynom
![]() (oder allgemeiner Polynom mit Koeffizienten in einen
Körper) besitzt genau dann ein multiplikatives Inverses, d.h. ist eine Einheit, wenn
(oder allgemeiner Polynom mit Koeffizienten in einen
Körper) besitzt genau dann ein multiplikatives Inverses, d.h. ist eine Einheit, wenn
![]() , d.h.
, d.h.
![]() konstant aber nicht 0 ist.
konstant aber nicht 0 ist.
Beweis. Sei
4.9 Folgerung.
Falls
![]() ein Integritätsbereich ist, so ist auch der Ring
ein Integritätsbereich ist, so ist auch der Ring
![]() der Polynome mit Koeffizienten in
der Polynome mit Koeffizienten in
![]() ein solcher.
ein solcher.
Beweis. Es seien
4.10 Bemerkung.
Wie bei ganzen Zahlen, können wir auch bei reellen Polynomen (oder allgemeiner
bei Polynomen mit Koeffizienten in einem Körper) die
Division mit Rest durchführen:
Wir fassen dazu die Koeffizienten
![]() als
als
![]() -te ``Ziffer''
von rechts gezählt auf.
Z.B. ist
-te ``Ziffer''
von rechts gezählt auf.
Z.B. ist
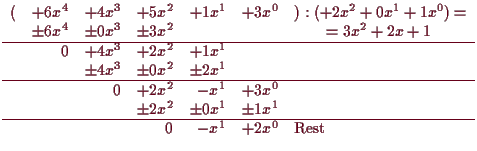
4.11 Horner-Schema.
Es sei
![]() ein Polynom
ein Polynom
![]() mit Koeffizienten aus
einem Ring
mit Koeffizienten aus
einem Ring
![]() und
und
![]() .
Division durch
.
Division durch
![]() mit Rest liefert ein Polynom
mit Rest liefert ein Polynom
![]() und Rest
und Rest
![]() mit
mit
![]() .
Wir versuchen nun eine Formel für Koeffizienten
.
Wir versuchen nun eine Formel für Koeffizienten
![]() und Rest
und Rest
![]() zu finden.
Es ist
zu finden.
Es ist
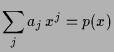 |
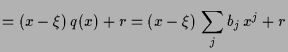 |
|
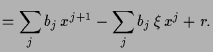 |
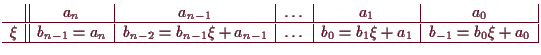
Induktive Anwendlung liefert das vollständige Horner-Schema
zur Darstellung
eines Polynoms
![]() als Linearkombination von Potenzen von
als Linearkombination von Potenzen von
![]() ,
d.h.
,
d.h.
![]() .
.
4.12 Definition.
Unter einer Nullstelle einer Funktion
![]() , versteht
man ein
, versteht
man ein
![]() mit
mit
![]() .
Falls
.
Falls
![]() ein Polynom ist, so spricht man auch von einer Wurzel
ein Polynom ist, so spricht man auch von einer Wurzel
![]() von
von
![]() .
.
4.13 Proposition.
Es sei
![]() ein Polynom und
ein Polynom und
![]() .
Dann gilt:
.
Dann gilt:
![]()
![]()
![]() teilt
teilt
![]() :
:
Beweis. Da
4.13a Folgerung. Koeffizientenvergleich.
Es sei
![]() ein Polynom vom Grad
ein Polynom vom Grad
![]() und
und
![]() ein
Integritätsbereich.
Dann besitzt
ein
Integritätsbereich.
Dann besitzt
![]() höchstens
höchstens
![]() Nullstellen.
Ist also
Nullstellen.
Ist also
![]() für unendlich viedle (oder zumindestens
für unendlich viedle (oder zumindestens
![]() viele
viele
![]() ), dann sind alle Koeffizienten
), dann sind alle Koeffizienten
![]() .
.
Beweis. Es seien
5.19 Proposition.
Es sei
![]() ein Polynom mit Koeffizienten in
ein Polynom mit Koeffizienten in
![]() und
und
![]() eine rationale Nullstelle
von
eine rationale Nullstelle
von
![]() mit relativ primen
mit relativ primen
![]() und
und
![]() .
Dann wird der führende Koeffizient von
.
Dann wird der führende Koeffizient von
![]() durch
durch
![]() und der 0-te
Koeffizient durch
und der 0-te
Koeffizient durch
![]() geteilt.
geteilt.
Dies kann dazu verwendet werden die rationalen Nullstellen eines Polynoms durch Probieren zu finden.
Beweis. Es sei also
4.14 Proposition. Vieta'scher Wurzelsatz.
Der
![]() -te Koeffizient von
-te Koeffizient von
![]() ist durch
ist durch
![]() gegeben, wobei
gegeben, wobei
![]() die
die
![]() -te elementarsymmetrische Funktion ist.
-te elementarsymmetrische Funktion ist.
Im Fall
Beweis. Wenn man
4.15 Euklid'ischer Algorithmus für Polynome.
Wie für ganze Zahlen können wir den Euklid'ische Algorithmus
auch dazu verwenden um einen ggT in
![]() zweier Polynome
zweier Polynome
![]() und
und
![]() zu bestimmen.
Wir müssen dazu nur rekursive Division mit Rest ausführen bis wir
bei Rest 0 landen. Der letzte Rest davor ist dann ein ggT.
zu bestimmen.
Wir müssen dazu nur rekursive Division mit Rest ausführen bis wir
bei Rest 0 landen. Der letzte Rest davor ist dann ein ggT.
Sei z.B.
![]() und
und
![]() .
Fortgesetze Division mit Rest liefert
.
Fortgesetze Division mit Rest liefert
Komposition von Polynomen.
Wenn wir Polynome als Abbildungen
![]() auffassen, so können wir diese
auch zusammensetzen, und erhalten somit allgemein eine Komposition:
auffassen, so können wir diese
auch zusammensetzen, und erhalten somit allgemein eine Komposition:
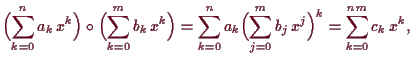
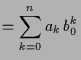 |
||
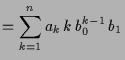 |
||
4.16 Bemerkung.
Jenes Polynom minimalen Grades, welches
an den Stellen
![]() die Werte
die Werte
![]() hat, heißt Interpolationspolynom und ist durch die
Lagrange'sche Interpolationsformel
hat, heißt Interpolationspolynom und ist durch die
Lagrange'sche Interpolationsformel
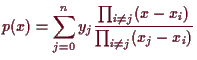
Beweis. Offensichtlich ist
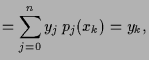 wobei wobei |
||
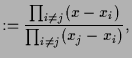 also also |
||
 |
![\includegraphics[scale=1]{pic-1042}](img1528.png)
4.17 Inklusions-Exklusions-Prinzip.
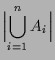 |
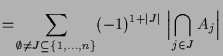 |
|
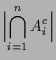 |
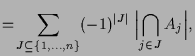 |
|
wobei wir 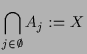 gesetzt haben. gesetzt haben. |
Mit
![\includegraphics[scale=0.7]{pic-1016}](img1535.png)
Beweis. Wir zeigen die erste Formel mittels Induktion nach
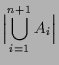 |
||
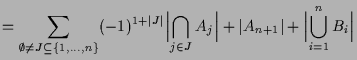 |
||
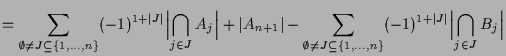 |
||
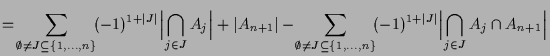 |
||
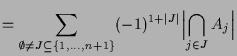 |
Die zweite Formel folgt mittels de Morgan'schen Gesetzen aus der ersten, denn
![\bgroup\color{demo}$\displaystyle \bigcap_{i=1}^n A_i^c=X\setminus \bigcup_{i=1}^n A_i.{\rm\quad[]}
$\egroup](img1555.png)
Andreas Kriegl 2002-02-01