Next: 20.2 Integration über meßbare Up: 20 Mehrfach Integrale Previous: 20 Mehrfach Integrale
20.1.1 Definition. Mehrdimensionale Integral.
Es sei
![]() beschränkt, wobei
beschränkt, wobei
![]() ein
ein ![]() -dimensionales Intervall (ein Rechteck, Quader oder Hyper-Quader)
ist, d.h.
-dimensionales Intervall (ein Rechteck, Quader oder Hyper-Quader)
ist, d.h.
![]() mit
mit
![]() ,...,
,...,
![]() .
Unter einer Zerlegung
.
Unter einer Zerlegung
![]() von
von
![]() verstehen wir
verstehen wir
![]() wobei
wobei
![]() eine Zerlegung von
eine Zerlegung von
![]() in Teilintervalle für
in Teilintervalle für
![]() ist.
Also besteht
ist.
Also besteht
![]() seinerseits aus
seinerseits aus
![]() -dimensionalen Teilintervallen
-dimensionalen Teilintervallen
![]() von
von
![]() .
Analog zum 1-dimensionalen Fall definieren wir die Obersumme und
Untersumme
der Funktion
.
Analog zum 1-dimensionalen Fall definieren wir die Obersumme und
Untersumme
der Funktion
![]() bzgl. der Zerlegung
bzgl. der Zerlegung
![]() als
als

Die Funktion
![]() heißt Riemann-integrierbar
und
heißt Riemann-integrierbar
und
![]() das Riemann-Integral von
das Riemann-Integral von
![]() (über
(über
![]() ),
falls
),
falls
![]() ,
d.h.
,
d.h.
![]()
![]() mit
mit
![]() .
.
20.1.2
Lebesgue'sche Integrabilitätskriterium.
Eine beschränkte Funktion
![]() auf einen mehrdimensionalen Intervall
auf einen mehrdimensionalen Intervall
![]() ist genau dann
ist genau dann
![]() -integrierbar, wenn
-integrierbar, wenn
![]() fast überall
stetig auf
fast überall
stetig auf
![]() ist.
ist.
Beweis.
![]()
![]() mit
mit
![]() .
.
![]()
![]()
![]() , d.h.
, d.h.
![]() mit
mit
![]() .
.
![]()
![]() ist offene
Überdeckung, also existiert eine endliche Teilüberdeckung
ist offene
Überdeckung, also existiert eine endliche Teilüberdeckung
![]() . Sei
. Sei
![]() eine
Zerlegung mit
eine
Zerlegung mit
![]() für ein
für ein
![]() .
Daß das geht, sieht man wie folgt:
Wegen der Dreiecksungleichung ist
.
Daß das geht, sieht man wie folgt:
Wegen der Dreiecksungleichung ist
![]() stetig und
stetig und
![]() auf
auf
![]() .
Also ist
.
Also ist
![]() stetig und
stetig und
![]() überall, und
folglich existiert ein
überall, und
folglich existiert ein
![]() mit
mit
![]() für alle
für alle
![]() , d.h. für jeden Quader
, d.h. für jeden Quader
![]() mit Durchmesser
mit Durchmesser
![]() und
Mittelpunkt
und
Mittelpunkt
![]() ist ein
ist ein
![]() und somit
und somit
![]() .
Dann ist
.
Dann ist
20.1.3 Satz von Fubini.
Es seien
![]() und
und
![]() zwei
kompakte Quader und
zwei
kompakte Quader und
![]()
![]() -integrierbar. Weiters sei
-integrierbar. Weiters sei
![]() auf
auf
![]()
![]() -integrierbar.
-integrierbar.
Dann ist
![]() auf
auf
![]()
![]() -integrierbar und es gilt:
-integrierbar und es gilt:
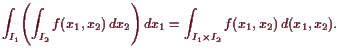
Beweis. Es sei
20.1.4 Folgerung.
Es seien
![]() und
und
![]() zwei
kompakte Quader und
zwei
kompakte Quader und
![]()
![]() -integrierbar. Weiters sei
-integrierbar. Weiters sei
![]() auf
auf
![]()
![]() -integrierbar
und
-integrierbar
und
![]() auf
auf
![]()
![]() -integrierbar.
-integrierbar.
Dann ist
![\begin{multline*}
\int_{I_1}\Biggl(\int_{I_2} f(x_1,x_2) dx_2\Biggr) dx_1 =
\...
...I_2}\Biggl(\int_{I_1} f(x_1,x_2) dx_1\Biggr) dx_2.{\rm\quad[]}
\end{multline*}](img3151.gif)
![\bgroup\color{proclaim}$\displaystyle \int_I f = \int_{a_1}^{b_1}\dots
\int_{a_p}^{b_p} f(x_1,\dots,x_p) dx_p \dots dx_1.{\rm\quad[]}
$\egroup](img3154.gif)
Beispiel.
Es sei
![]() gegeben durch
gegeben durch
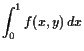 |
||
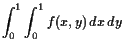 |
||
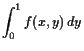 |
Andreas Kriegl 2002-07-01