Nächste Seite: 4.2 Unbestimmte Integrale Aufwärts: 4 Integralrechnung Vorherige Seite: 4 Integralrechnung Inhalt Index
4.1.1 Definition.
Es sei
![]() eine beschränkte Abbildung auf einem kompakten
Intervall
eine beschränkte Abbildung auf einem kompakten
Intervall
![]() mit Werten in einem endlich dimensionalen Vektorraum
mit Werten in einem endlich dimensionalen Vektorraum
![]() .
Es sei
.
Es sei
![]() eine endliche Zerlegung von
eine endliche Zerlegung von
![]() in Teilintervalle
in Teilintervalle
![]() .
Als Obersumme von
.
Als Obersumme von
![]() bzgl. der Zerlegung
bzgl. der Zerlegung
![]() bezeichnet man
bezeichnet man
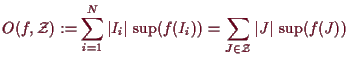
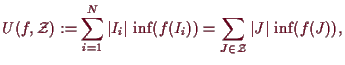
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-4-01}\egroup](img1628.png)
Weiters sei
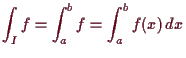
4.1.2 Lemma.
Jede monotone Funktion und jede stetige Funktion ist Riemann-integrierbar.
Man sieht leicht ein, daß monotone Funktionen nur Sprungstellen als Unstetigkeitsstellen besitzen können, und davon höchsten abzählbar viele vorhanden sein können.
Beweis. (1) O.B.d.A. sei
(2) Sei nun
![]() stetig, dann ist
stetig, dann ist
![]() gleichmäßig stetig nach 2.3.5,
also existiert zu
gleichmäßig stetig nach 2.3.5,
also existiert zu
![]() ein
ein
![]() mit
mit
![]() für
für
![]() .
Sei nun
.
Sei nun
![]() eine äquidistante Zerlegung wie zuvor mit Schrittweite
eine äquidistante Zerlegung wie zuvor mit Schrittweite
![]() . Für
. Für
![]() ist dann
ist dann
![]() und somit
und somit
![]() .
Also gilt
.
Also gilt
![]() .
[]
.
[]
4.1.3 Beispiele.
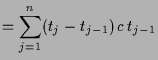 |
||
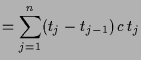 |
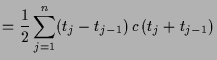 |
||
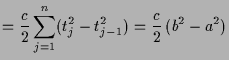 |
Ein Kriterium für die Integrierbarkeit ist folgender Satz den wir ohne Beweis angeben.
4.1.4 Lebesgue'sches Integrabilitätskriterium.
Eine beschränkte Funktion ist genau dann
Riemann-integrierbar
wenn die Menge der Punkte
![]() in denen sie unstetig ist
eine Lebesgue-Nullmenge ist.
in denen sie unstetig ist
eine Lebesgue-Nullmenge ist.
Dabei heißt eine Teilmenge
Z.B. ist jede abzählbare Menge eine Nullmenge, denn sei
![]() und
und
![]() . Dann ist
. Dann ist
![]() und
und
![]() .
.
4.1.5 Beispiel.
Die Dirichlet'sche Sprungfunktion
![]() ist überall unstetig, also auf
ist überall unstetig, also auf
![]() nicht integrierbar.
nicht integrierbar.
Hingegen ist die Funktion
![]() welche gegeben ist durch
welche gegeben ist durch
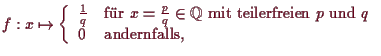
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-4-02}\egroup](img1629.png)
4.1.6 Lemma.
Die Riemann-integrierbare Funktionen bilden einen Vektorraum. Integrieren ist linear.
Beweis. Es ist
4.1.7 Lemma.
Produkte Riemann-integrierbarer Funktionen sind Riemann-integrierbar.
Ebenso beschränkte Quotienten.
Beachte jedoch, daß dies keine Formel zur Berechnung des Integrals eines Produktes aus jenen der Teile liefert.
Beweis. Dies folgt leicht aus dem Lebesgue'schen Integrabilitätskriterium 4.1.4. []
4.1.8 Lemma.
Integrieren ist additiv in den Grenzen.
Beweis. Es seien
4.1.9 Lemma.
Integrieren ist monoton.
Beweis. Aus
4.1.10 Mittelwertsatz der Integralrechnung.
Es sei
![]() für alle
für alle
![]() und
und
![]() integrierbar.
Dann ist
integrierbar.
Dann ist
![]() .
.
Beweis. Dies folgt aus 4.1.9, da
Andreas Kriegl 2001-07-01