4.2 Unbestimmte Integrale

4.2.1 Definition. Unbestimmte Integral.
Es sei $\bgroup\color{demo}$ f:[a,b]\to\mathbb{R}$\egroup$ Riemann-integrierbar. Nach dem Lebesgue'schen Integrabilitätskriterium 4.1.4 existiert dann für jedes $\bgroup\color{demo}$ x\in[a,b]$\egroup$ auch $\bgroup\color{demo}$ F(x):=\int_a^x f(t)\,dt$\egroup$ . Diese Abbildung $\bgroup\color{demo}$ F:[a,b]\to\mathbb{R}$\egroup$ heißt unbestimmtes Integral von $\bgroup\color{demo}$ f$\egroup$ .

4.2.2 Hauptsatz.
Das unbestimmte Integral $\bgroup\color{demo}$ F$\egroup$ jeder Riemann-integrierbaren Funktion $\bgroup\color{demo}$ f$\egroup$ ist stetig. Ist der Integrand $\bgroup\color{demo}$ f$\egroup$ stetig, so ist $\bgroup\color{demo}$ F$\egroup$ differenzierbar mit Ableitung $\bgroup\color{demo}$ F'=f$\egroup$ .

Umgekehrt sei $\bgroup\color{demo}$ F$\egroup$ stetig differenzierbar mit Ableitung $\bgroup\color{demo}$ f:=F'$\egroup$ . Dann ist $\bgroup\color{demo}$ f$\egroup$ Riemann-integrierbar und $\bgroup\color{demo}$ \int_a^b f(x)\,dx=F(b)-F(a)=:F(x)\vert _{x=a}^{b}$\egroup$ .

Jede Funktion $\bgroup\color{demo}$ F$\egroup$ die $\bgroup\color{demo}$ F'=f$\egroup$ erfüllt heißt Stammfunktion von $\bgroup\color{demo}$ f$\egroup$ . Insbesonders ist $\bgroup\color{demo}$ \int_a^b f(x)\,dx=F(x)\vert _{x=a}^b$\egroup$ für jede Stammfunktion $\bgroup\color{demo}$ F$\egroup$ von $\bgroup\color{demo}$ f$\egroup$ und man schreibt auch $\bgroup\color{demo}$ \int f=\int f(t)\,dt$\egroup$ für die (Familie der) Stammfunktion(en) von $\bgroup\color{demo}$ f$\egroup$ . Der Hauptsatz besagt also, daß integrieren und differenzieren im wesentlichen, d.h. bis auf Addition einer Konstanten, invers zueinander sind.

Beweis. Es ist $\bgroup\color{demo}$ F(x+h)-F(x)=\int_x^{x+h} f(t)\,dt$\egroup$ , also $\bgroup\color{demo}$ \vert F(x+h)-F(x)\vert\leq \vert h\vert\,sup\{\vert f(t)\vert:t\}$\egroup$ nach 4.1.10 und somit $\bgroup\color{demo}$ F$\egroup$ (Lipschitz)-stetig, da $\bgroup\color{demo}$ f$\egroup$ beschränkt ist.

Ist $\bgroup\color{demo}$ f$\egroup$ zusätzlich stetig, so existiert zu $\bgroup\color{demo}$ \varepsilon >0$\egroup$ ein $\bgroup\color{demo}$ \delta >0$\egroup$ s.d. $\bgroup\color{demo}$ \vert f(t)-f(x)\vert\leq\varepsilon $\egroup$ für alle $\bgroup\color{demo}$ \vert t-x\vert\leq \delta $\egroup$ und damit ist

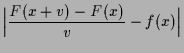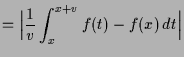$\displaystyle \Bigl\vert\frac{F(x+v)-F(x)}{v}-f(x)\Bigr\vert$	$\displaystyle =\Bigl\vert\frac1v \int_{x}^{x+v} f(t)-f(x)\,dt\Bigr\vert$
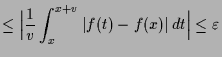	$\displaystyle \leq \Bigl\vert\frac1v\int_{x}^{x+v} \vert f(t)-f(x)\vert\,dt\Bigr\vert \leq \varepsilon$

für $\bgroup\color{demo}$ \vert v\vert\leq\delta $\egroup$ . Also ist $\bgroup\color{demo}$ F'(x)=\lim_{v\to 0}\frac{F(x+v)-F(x)}{v}=f(x)$\egroup$ .

$\bgroup\color{demo}\includegraphics[scale=.7]{pic-4-03}\egroup$

Ist $\bgroup\color{demo}$ f$\egroup$ also stetig, so ist $\bgroup\color{demo}$ F:x\mapsto \int_a^x f(y)\,dy$\egroup$ eine Stammfunktion von $\bgroup\color{demo}$ f$\egroup$ .

Nach Voraussetzung ist $\bgroup\color{demo}$ F$\egroup$ eine Stammfunktion von $\bgroup\color{demo}$ f$\egroup$ und nach dem 1. Teil ist $\bgroup\color{demo}$ G:x\mapsto \int_a^x f(t)\,dt$\egroup$ ebenfalls eine Stammfunktion, also ist die Ableitung von $\bgroup\color{demo}$ F-G$\egroup$ gleich 0 und damit nach Mittelwertsatz $\bgroup\color{demo}$ F-G$\egroup$ konstant, also $\bgroup\color{demo}$ \int_a^b f(x)\, dx=G(b)=G(b)-G(a)=F(b)-F(a)$\egroup$ . []

4.2.3 Beispiele von Stammfunktionen.

$\int x^a\,dx =\frac{x^{a+1}}{a+1}+C$ für alle $\mathbb{Q}\ni a\ne 1$ .
$\int \sin(x)\,dx =-\cos(x)+C$
$\int \cos(x)\,dx =\sin(x)+C$
$\int \frac1{\cos(x)^2}\,dx =\tan(x)+C$
$\int \frac1{\sin(x)^2}\,dx =-\cot(x)+C$
$\int \frac1{\sqrt{1-x^2}}\,dx =\arcsin(x)+C$
$\int \frac1{1+x^2}\,dx =\arctan(x)+C$
$\int f+\lambda \,g=\int f + \lambda \int g$
$\int f\,g'=f\,g-\int f'\,g$ (partielle Integration).
Z.B. $\int x\,\cos(x)\,dx=x\,\sin(x)-\int 1\,\sin(x)\,dx=x\,\sin(x)+\cos(x)+C$ .
$\int F'(g(t))\,g'(t)\,dt=F\o g+C$
$\int_{g(a)}^{g(b)}f(t)\,dt=\int_a^b f(g(t))\,g'(t)\,dt$
(]Substitutionsformel für unbestimmte Integrale).
$\int_{g(x_0)}^{g(x_1)}f(y)\,dy=\int_{x_0}^{x_1}f(g(x))\,g'(x)\,dx$
(Substitutionsformel für bestimmte Integrale), denn aus dem vorigen Punkt folgt

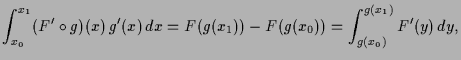
$\displaystyle \int_{x_0}^{x_1} (F'\o g)(x)\,g'(x)\,dx = F(g(x_1))-F(g(x_0)) =\int_{g(x_0)}^{g(x_1)} F'(y)\,dy,$
mit einer Stammfunktion von .
Z.B. $\int_1^2 x\,\sqrt{1+x^2}\,dx=\int_2^5 \sqrt{u}\,\frac{du}{2} =\frac{u^{3/2}}{3}\vert _2^5=\frac{5\sqrt{5}-2\sqrt{2}}3$ .

4.2.4 Definition. Logarithmus.
Es sei der natürliche Logarithmus definiert durch $\bgroup\color{demo}$ \ln(x):=\int_1^x \frac1{y}\,dy$\egroup$ . Dann ist $\bgroup\color{demo}$ \ln:\mathbb{R}^+\to\mathbb{R}$\egroup$ eine Stammfunktion zu $\bgroup\color{demo}$ x\mapsto \frac1x$\egroup$ also insbesonders streng monoton wachsend. Weiters ist $\bgroup\color{demo}$ \ln(1)=\int_1^1 \frac1y\,dy=0$\egroup$ und

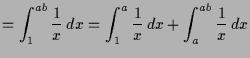$\displaystyle \ln(ab)$	$\displaystyle = \int_1^{ab} \frac1x\,dx = \int_1^a \frac1x\,dx + \int_a^{ab}\frac1x\,dx$
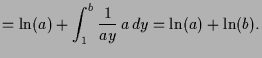	$\displaystyle = \ln(a) + \int_1^b \frac1{ay}\,a\,dy=\ln(a)+\ln(b).$

Folglich ist $\bgroup\color{demo}$ \ln(a^n)=n\,\ln(a)$\egroup$ für alle $\bgroup\color{demo}$ n\in\mathbb{N}$\egroup$ und weiters $\bgroup\color{demo}$ \ln(a^x)=x\,\ln(a)$\egroup$ für $\bgroup\color{demo}$ x\in\mathbb{Q}$\egroup$ . Denn sei $\bgroup\color{demo}$ x=\frac{p}{q}$\egroup$ , dann ist $\bgroup\color{demo}$ \ln(a)=\ln((a^{1/q})^q)=q\,\ln(a^{1/q})$\egroup$ , also $\bgroup\color{demo}$ \ln(a^{1/q})=\frac1q\,\ln(a)$\egroup$ und somit $\bgroup\color{demo}$ \ln(a^x)=x\,\ln(a)$\egroup$ für $\bgroup\color{demo}$ x>0$\egroup$ . Für $\bgroup\color{demo}$ x<0$\egroup$ ist $\bgroup\color{demo}$ \ln(a^x)=\ln(1/a^{-x})=-\ln(a^{-x})=-(-x)\,\ln(a)=x\,\ln(a)$\egroup$ . Schließlich ist $\bgroup\color{demo}$ \lim_{x\to+{\infty}}\ln(x)=+{\infty}$\egroup$ , denn $\bgroup\color{demo}$ \int_1^n \frac1x\,dx\geq \sum_{k=2}^n\frac1k\to{\infty}$\egroup$ . Wegen $\bgroup\color{demo}$ \ln(1/x)=-\ln(x)$\egroup$ ist $\bgroup\color{demo}$ \lim_{x\to 0+}\ln(x)=-{\infty}$\egroup$ .

Nach de Sätzen 2.4.4 und 3.3.4 über inverse Funktionen existiert somit die differenzierbare Umkehrfunktion $\bgroup\color{demo}$ \exp:\mathbb{R}\to\mathbb{R}^+$\egroup$ (genannte Exponentialfunktion) mit $\bgroup\color{demo}$ \exp'(x)=\frac1{\ln'(\exp(x))}=\exp(x)$\egroup$ . Weiters folgt aus den Aussagen für $\bgroup\color{demo}$ \ln$\egroup$ , daß $\bgroup\color{demo}$ \exp(x+y)=\exp(x)\cdot\exp(y)$\egroup$ und $\bgroup\color{demo}$ \exp(0)=1$\egroup$ . Es ist

$\displaystyle (1+\frac1n)^n=\exp(\ln((1+\frac1n)^n))=\exp(n\,\ln(1+\frac1n))$

und somit

$\displaystyle e$	$\displaystyle =\lim_{n\to{\infty}}(1+\frac1n)^n =\exp(\lim_{n\to{\infty}}n\,\ln(1+\frac1n))$
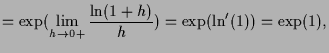	$\displaystyle =\exp(\lim_{h\to 0+}\frac{\ln(1+h)}h)=\exp(\ln'(1))=\exp(1),$

d.h. $\bgroup\color{demo}$ \exp(x)=e^x$\egroup$ für alle $\bgroup\color{demo}$ x\in\mathbb{Q}$\egroup$ .

4.2.5 Definition. Allgemeine Potenz und Logarithums.
Sei nun $\bgroup\color{demo}$ a\in\mathbb{R}^+$\egroup$ . Dann setzen wir

$\bgroup\color{demo}$\displaystyle a^x := \exp(x\,\ln(a))$\egroup$ für $\bgroup\color{demo}$\displaystyle x\in\mathbb{R}$\egroup$

Und für $\bgroup\color{demo}$ a\ne 1$\egroup$ heißt die Umkehrfunktion zu $\bgroup\color{demo}$ x\mapsto a^x$\egroup$ der Logarithmus $\bgroup\color{demo}$ \log_a$\egroup$ zur Basis $\bgroup\color{demo}$ a$\egroup$ .

4.2.6 Definition.
Es sei $\bgroup\color{demo}$ f:\mathbb{R}\to\mathbb{R}$\egroup$ eine Funktion. Dann ist $\bgroup\color{demo}$ g:x\mapsto \frac{f(x)+f(-x)}2$\egroup$ eine gerade und $\bgroup\color{demo}$ u:x\mapsto \frac{f(x)-f(-x)}2$\egroup$ eine ungerade Funktion mit $\bgroup\color{demo}$ f=g+h$\egroup$ .

Wenden wir dies insbesonders auf die Funktione $\bgroup\color{demo}$ f:=\exp$\egroup$ an, so erhalten wir den Sinushyperbolicus $\bgroup\color{demo}$ \sinh(x):=\frac{e^x-e^{-x}}2$\egroup$ , und und den Cosinushyperbolicus $\bgroup\color{demo}$ \cosh(x):=\frac{e^x+e^{-x}}2$\egroup$ . In Analogie zu den üblichen Winkelfunktionen definieren wir den Tangenshyperbolicus als $\bgroup\color{demo}$ \tanh(x):=\frac{\sinh(x)}{\cosh(x)}$\egroup$ . Die dazugehörenden Umgehrfunktionen heißen Areasinushyperbolicus $\bgroup\color{demo}$ \operatorname{Arsinh}$\egroup$ , Areacosinushyperbolicus $\bgroup\color{demo}$ \operatorname{Arcosh}$\egroup$ und $\bgroup\color{demo}$ {\textcolor{index}{Areatangenshyperbolicus}}\index{Areatangenshyperbolicus}\operatorname{Artanh}$\egroup$ . Die Nahmensgebung begründet sich darin, daß die Punkte $\bgroup\color{demo}$ (x,y)$\egroup$ eines Astes der gleichseitigen Hyperbel $\bgroup\color{demo}$ x^2-y^2=1$\egroup$ sich durch $\bgroup\color{demo}$ x=\cosh(t)$\egroup$ , $\bgroup\color{demo}$ y=\sinh(t)$\egroup$ parametrisieren lassen wobei $\bgroup\color{demo}$ t$\egroup$ die Fläche des Hyperbelsektors bezeichnet.

4.2.7 Bemerkung.
Folgende rationale Ausdrücke können wir integrieren:

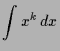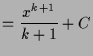$\displaystyle \int x^k\,dx$	$\displaystyle = \frac{x^{k+1}}{k+1}+C$ für $\displaystyle k\ne -1$
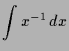$\displaystyle \int x^{-1}\,dx$	$\displaystyle = \ln(x)+C$
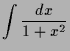$\displaystyle \int \frac{dx}{1+x^2}$	$\displaystyle = \arctan(x)+C$

Unser Ziel ist es nun beliebige rationale Funktionen $\bgroup\color{demo}$ x\mapsto \frac{P(x)}{Q(x)}$\egroup$ mit Polynomen $\bgroup\color{demo}$ P$\egroup$ und $\bgroup\color{demo}$ Q$\egroup$ zu berechnen. Wir können natürlich Division mit Rest durchführen und damit ein Polynom abspalten um eine rationale Funktion mit $\bgroup\color{demo}$ \deg(P)<\deg(Q)$\egroup$ zu erhalten.

4.2.8 Proposition. Partialbruchzerlegung im Komplexen.

Es seien $\bgroup\color{proclaim}$ P$\egroup$ und $\bgroup\color{proclaim}$ Q$\egroup$ Polynome mit komplexen Koeffizienten und $\bgroup\color{proclaim}$ \operatorname{grad}(P)<\operatorname{grad}(Q)$\egroup$ . Weiters seien $\bgroup\color{proclaim}$ \alpha _1,\dots,\alpha _n$\egroup$ die verschiedenen Nullstellen von $\bgroup\color{proclaim}$ Q$\egroup$ und $\bgroup\color{proclaim}$ d_1,\dots,d_n$\egroup$ ihre Vielfachheit. Dann ist

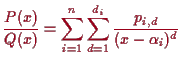
$\bgroup\color{proclaim}$\displaystyle \frac{P(x)}{Q(x)} = \sum_{i=1}^n \sum_{d=1}^{d_i}\frac{p_{i,d}}{(x-\alpha _i)^d} $\egroup$

mit gewisssen eindeutig bestimmten Koeffizienten $\bgroup\color{proclaim}$ p_{i,d}\in\mathbb{C}$\egroup$ .

Beweis. Nach Voraussetzung ist

$\bgroup\color{proclaim}$\displaystyle Q(x)=(x-\alpha _1)^{d_1}\cdot Q_1(x) $\egroup$

und somit $\bgroup\color{demo}$ \frac{P(x)}{Q(x)}=\frac{P(x)}{(x-\alpha _1)^{d_1}Q_1(x)}$\egroup$ mit $\bgroup\color{demo}$ \lim_{x\to \alpha _1}\frac{P(x)}{Q_1(x)}=\frac{P(\alpha _1)}{Q_1(\alpha _1)}$\egroup$ . Daher ist

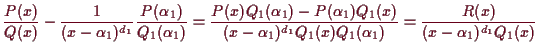
$\bgroup\color{demo}$\displaystyle \frac{P(x)}{Q(x)}-\frac1{(x-\alpha _1)^{d_1}}\... ... _1)^{d_1}Q_1(x)Q_1(\alpha _1)} =\frac{R(x)}{(x-\alpha _1)^{d_1}Q_1(x)} $\egroup$

mit $\bgroup\color{demo}$ R(x):=\frac{P(x)Q_1(\alpha _1)-P(\alpha _1)Q_1(x)}{Q_1(\alpha _1)}$\egroup$ und $\bgroup\color{demo}$ R(\alpha _1)=0$\egroup$ . Also ist das Polynom $\bgroup\color{demo}$ R$\egroup$ durch $\bgroup\color{demo}$ (x-\alpha _1)$\egroup$ teilbar, d.h. $\bgroup\color{demo}$ R(x)=(x-\alpha _1)\cdot R_1(x)$\egroup$ und somit ist

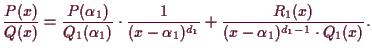
$\bgroup\color{demo}$\displaystyle \frac{P(x)}{Q(x)}=\frac{P(\alpha _1)}{Q_1(\alp... ...x-\alpha _1)^{d_1}} + \frac{R_1(x)}{(x-\alpha _1)^{d_1-1}\cdot Q_1(x)}. $\egroup$

Nun folgt das Resultat mittels Induktion. []

Wir können nun die Partialbruchzerlegung verwenden um rationale Funktionen zu integrieren.

4.2.9 Beispiel.
Es sei die rationale Funktion $\bgroup\color{demo}$ f:x\mapsto\frac{x^2+1}{x^3-2x^2+x}$\egroup$ gegeben. Die Nullstellen des Nenners sind 0 und $\bgroup\color{demo}$ 1$\egroup$ mit Vielfachheiten $\bgroup\color{demo}$ 1$\egroup$ und $\bgroup\color{demo}$ 2$\egroup$ also $\bgroup\color{demo}$ x^3-2x^2+x=x(x-1)^2$\egroup$ . Es muß also nach 4.2.8 eine Darstellung der Form

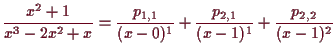
$\bgroup\color{demo}$\displaystyle \frac{x^2+1}{x^3-2x^2+x} = \frac{p_{1,1}}{(x-0)^1} + \frac{p_{2,1}}{(x-1)^1} + \frac{p_{2,2}}{(x-1)^2} $\egroup$

existieren. Ausmultiplizieren der Nenner liefert:

$\bgroup\color{demo}$\displaystyle x^2+1=p_{1,1}\,(x-1)^2 + p_{2,1}\,x(x-1) + p_{2,2}\,x, $\egroup$

also

$\bgroup\color{demo}$\displaystyle (p_{1,1}+p_{2,1}-1)\,x^2 + (-2p_{1,1}-p_{2,1}+p_{2,2})\,x+(p_{1,1}-1)=0. $\egroup$

Es müssen also alle Koeffizienten dieses Polynoms 0 sein, d.h.

$\displaystyle p_{1,1}+p_{2,1}$	$\displaystyle = 1$
$\displaystyle p_{2,2}-2p_{1,1}-p_{2,1}$	$\displaystyle = 0$
$\displaystyle p_{1,1}$	$\displaystyle = 1$

Die Lösung dieses linearen Gleichungssystems ist

$\bgroup\color{demo}$\displaystyle p_{1,1} = 1,\quad p_{2,1} = 0$\egroup$ und $\bgroup\color{demo}$\displaystyle p_{2,2}=2, $\egroup$

d.h.

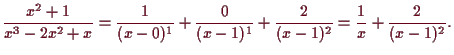
$\bgroup\color{demo}$\displaystyle \frac{x^2+1}{x^3-2x^2+x} = \frac{1}{(x-0)^1} + \frac{0}{(x-1)^1} + \frac{2}{(x-1)^2} = \frac1{x} + \frac{2}{(x-1)^2}. $\egroup$

Somit ist

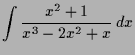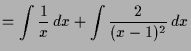$\displaystyle \int \frac{x^2+1}{x^3-2x^2+x}\,dx$	$\displaystyle = \int \frac1{x}\,dx + \int \frac{2}{(x-1)^2}\,dx$
	$\displaystyle = \ln(x) - \frac{2}{x-1} + C.$

4.2.10 Proposition. Partialbruchzerlegung im Reellen.

Es seien $\bgroup\color{demo}$ P$\egroup$ und $\bgroup\color{demo}$ Q$\egroup$ Polynome mit reellen Koeffizienten und $\bgroup\color{demo}$ \operatorname{grad}(P)\leq\operatorname{grad}(Q)$\egroup$ . Weiters seien $\bgroup\color{demo}$ \alpha _1,\dots,\alpha _k$\egroup$ die verschiedenen reellen Nullstellen von $\bgroup\color{demo}$ Q$\egroup$ und $\bgroup\color{demo}$ d_1,\dots,d_k$\egroup$ ihre Vielfachheit. Seien schließlich $\bgroup\color{demo}$ a_1\pm i\,b_1,\dots,a_j\pm i\, b_j$\egroup$ die echt komplexen verschiedenen Nullstellen von $\bgroup\color{demo}$ Q$\egroup$ und $\bgroup\color{demo}$ e_1,\dots,e_j$\egroup$ ihre Vielfachheit. Dann ist

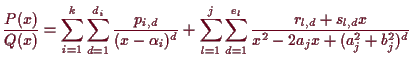
$\bgroup\color{demo}$\displaystyle \frac{P(x)}{Q(x)} = \sum_{i=1}^k \sum_{d=1}^{d... ...sum_{d=1}^{e_l}\frac{r_{l,d}+s_{l,d}x}{x^2 - 2 a_j x + (a_j^2+b_j^2)^d} $\egroup$

mit gewissen eindeutig bestimmten reellen Koeffizienten $\bgroup\color{demo}$ p_{i,d}$\egroup$ , $\bgroup\color{demo}$ r_{j,d}$\egroup$ und $\bgroup\color{demo}$ s_{j,j}$\egroup$ .

Andreas Kriegl 2001-07-01