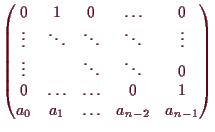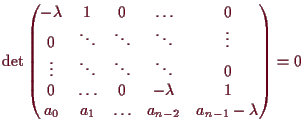4.4.1 Definition.
Unter einer gewöhnlichen Differentialgleichung 1.ter Ordnung
versteht man eine Gleichung der Form
wo
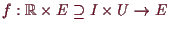 für ein offenes Intervall
für ein offenes Intervall
 in
in
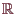 ,
welches
,
welches
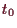 enthält
und eine offene Umgebung
enthält
und eine offene Umgebung
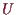 von
von
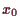 in einem endlich dimensionalen
Vektorraum
in einem endlich dimensionalen
Vektorraum
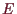 und wobei die Lösung
und wobei die Lösung
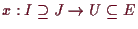 eine
differenzierbare Kurve auf einen offenen Intervall
eine
differenzierbare Kurve auf einen offenen Intervall
 sein soll, welches
sein soll, welches
 enthält.
enthält.
4.4.4 Picard-Lindelöf Theorem.
Es sei
![\bgroup\color{demo}$ f:[-a,a]\times B\to E$\egroup](img1837.png) stetig
und bzgl. der zweiten Variable Lipschitz,
wobei
stetig
und bzgl. der zweiten Variable Lipschitz,
wobei
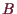 der abgeschlossene Ball im Euklidischen Raum
der abgeschlossene Ball im Euklidischen Raum
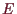 mit Mittelpunkt
mit Mittelpunkt
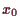 und Radius
und Radius
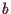 sei.
Weiters, sei
sei.
Weiters, sei
 .
Dann existiert eine eindeutige (iterative erhaltbare) Lösung
.
Dann existiert eine eindeutige (iterative erhaltbare) Lösung
![\bgroup\color{demo}$ x':[-a_1,a_1]\to B$\egroup](img1839.png) der Differential-Gleichung
der Differential-Gleichung
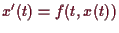
mit
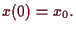
Beweis.
Aus
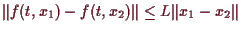 folgert man
folgert man
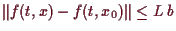 und da
und da
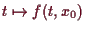 stetig ist erhalten wir
stetig ist erhalten wir
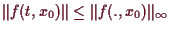 und somit
Um den Banach'schen Fixpunkt-Satz 2.4.6 anzuwenden, übersetzen wir die
Differential-Gleichung in eine äquivalente(!)
Integral Gleichung auf dem abgeschlossenen Ball
und somit
Um den Banach'schen Fixpunkt-Satz 2.4.6 anzuwenden, übersetzen wir die
Differential-Gleichung in eine äquivalente(!)
Integral Gleichung auf dem abgeschlossenen Ball
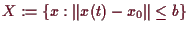 des vollständig metrischen Raumes
des vollständig metrischen Raumes
![\bgroup\color{demo}$ C([-a_1,a_1],E)$\egroup](img1848.png) .
.
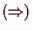 Aus
Aus
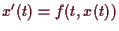 und
und
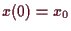 erhalten wir mittels dem Hauptsatz
erhalten wir mittels dem Hauptsatz
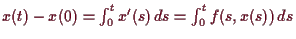 . Also ist
. Also ist
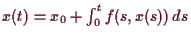 .
.
 Aus
Aus
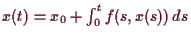 erhalten wir
welches gegen
erhalten wir
welches gegen
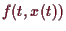 konvergiert wegen dem ersten Hauptsatz.
konvergiert wegen dem ersten Hauptsatz.
Die entsprechenden Integral-Operatoren
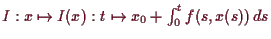 lassen
lassen
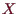 invariant, denn für
invariant, denn für
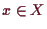 und
und
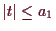 gilt
gilt
Und wenn man die äquivalente Norm
![\bgroup\color{demo}$ \Vert x\Vert:=\max\{\Vert x(t)\Vert e^{-2Lt}:t\in [-a_1,a_1]\}$\egroup](img1858.png) verwendet, sind sie eine
verwendet, sind sie eine
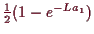 -Kontraktion, denn
-Kontraktion, denn
Also ist der Banach'sche Fixpunktsatz
anwendbar und wenn man mit einer beliebigen Funktion in
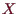 z.B. der konstant
z.B. der konstant
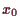 startet und rekursiv
startet und rekursiv
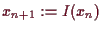 definiert. Dann konvergiert
definiert. Dann konvergiert
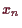 in
in
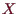 gegen den eindeutigen Fixpunkt
gegen den eindeutigen Fixpunkt
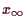 , die Lösung der Differentialgleichung.
[]
, die Lösung der Differentialgleichung.
[]
4.4.5 Beispiel.
Es sei
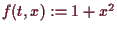 .
Die Lösung
.
Die Lösung
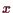 der Differentialgleichung
der Differentialgleichung
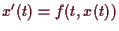 mit
Anfangsbedingung
mit
Anfangsbedingung
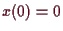 können wir mittels Separation der Variablen
bestimmen:
können wir mittels Separation der Variablen
bestimmen:
Die Lösung existiert somit nur auf den Intervall
 ganz im Unterschied zur global definierten Funktion
ganz im Unterschied zur global definierten Funktion
Für lineare Differentialgleichungen hingegen
passiert dieses Schrumpfen des Definitionsbereiches nicht:
4.4.6 Folgerung (Lineare Differential-Gleichung).
Es sei
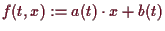 ,
dann existieren die Lösungen dort wo
,
dann existieren die Lösungen dort wo
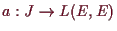 und
und
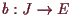 stetig sind. []
stetig sind. []
4.4.7 Bemerkung.
- Falls
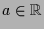 konstant und
konstant und  ist, dann ist die Lösung
ist, dann ist die Lösung
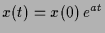 .
In der Tat können wir wieder Separation der Variablen durchführen und erhalten:
.
In der Tat können wir wieder Separation der Variablen durchführen und erhalten:
- Dies gilt auch für
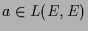 , wobei
, wobei
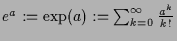 für alle
für alle 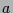 konvergiert.
konvergiert.
- Falls
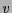 ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert 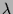 von
von 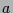 ist, d.h.
ist, d.h.
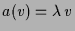 gilt,
so liefert eine Variation der Konstanten
den Ansatz
gilt,
so liefert eine Variation der Konstanten
den Ansatz
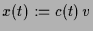 . Dies ist genau dann eine Lösung der
Differentialgleichung
. Dies ist genau dann eine Lösung der
Differentialgleichung
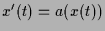 , wenn
, wenn
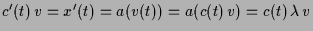 ,
also
,
also
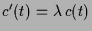 und somit
und somit
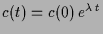 ist.
ist.
Beachte, daß jede Linearkombination von Lösungen einer homogenen
linearen Differentialgleichung selbst wieder eine Lösung ist.
Wenn also
 Eigenvektoren von
Eigenvektoren von 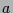 mit Eigenwerten
mit Eigenwerten
 sind, so ist auch
sind, so ist auch
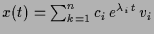 eine Lösung zum Anfangswert
eine Lösung zum Anfangswert
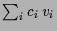 . Wenn die
. Wenn die 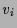 eine Basis bilden, so kann daraus jede
Lösung berechnet werden.
eine Basis bilden, so kann daraus jede
Lösung berechnet werden.
- Betrachten wir nun insbesonders den 2-dimensionalen Fall
einer homogenen lineare Differentialgleichung
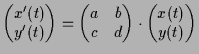
Es seien 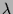 und
und 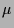 die beiden Eigenwerte dieser
die beiden Eigenwerte dieser 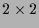 -Matrix
-Matrix 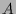 und
und 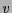 und
und 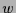 zugehörige Eigenvektoren. Dann können die folgenden Fälle auftreten:
zugehörige Eigenvektoren. Dann können die folgenden Fälle auftreten:
-
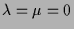 und
und 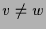 . Dann ist
. Dann ist  und alle Lösungen konstant.
und alle Lösungen konstant.
-
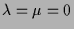 und
und  . Dies ist z.B. für
. Dies ist z.B. für  ,
,  der Fall, also für
die Differentialgleichung
der Fall, also für
die Differentialgleichung
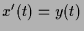 ,
, 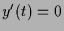 , d.h.
, d.h.
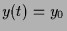 und
und
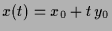 . Die Lösungskurven sind also
affine Geraden parallel zum Eigenvektor.
. Die Lösungskurven sind also
affine Geraden parallel zum Eigenvektor.
-
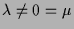 . Dies ist z.B. für
. Dies ist z.B. für  ,
,  der Fall, also
für die Differentialgleichung
der Fall, also
für die Differentialgleichung
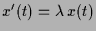 ,
, 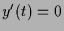 , d.h.
, d.h.
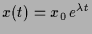 und
und 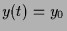 . Die Lösungskurven sind also durch die
Exponentialfunktion parametrisierte Halbgeraden parallel zum Eigenvektor
. Die Lösungskurven sind also durch die
Exponentialfunktion parametrisierte Halbgeraden parallel zum Eigenvektor 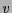 .
Je nach dem ob
.
Je nach dem ob
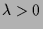 oder
oder
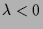 geht die Lösung für
geht die Lösung für
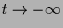 oder
oder
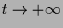 gegen die
gegen die 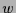 -Achse.
-Achse.
-
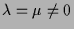 und
und 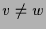 .
Dann ist
.
Dann ist
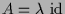 und die Lösungen sind
und die Lösungen sind
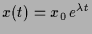 ,
,
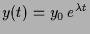 parametrisieren also gerade die Halbstrahlen durch 0.
Je nach dem ob
parametrisieren also gerade die Halbstrahlen durch 0.
Je nach dem ob
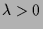 oder
oder
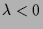 geht die Lösung für
geht die Lösung für
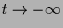 oder
oder
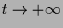 gegen 0.
gegen 0.
![\bgroup\color{demo}\includegraphics[scale=.3]{pic-4-05a}\egroup](img2038.png)
-
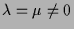 und
und  . Dies ist z.B. für
. Dies ist z.B. für
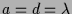 ,
,  ,
,  der Fall,
also für
der Fall,
also für
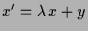 ,
,
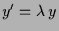 , d.h.
, d.h.
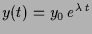 und
und
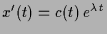 wobei
wobei
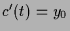 ist, also
ist, also
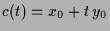 .
Die Lösungskurven gehen für
.
Die Lösungskurven gehen für
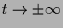 gegen 0 und
gegen 0 und 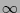 und schneiden
dabei die
und schneiden
dabei die 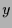 -Achse zum Zeitpunkt
-Achse zum Zeitpunkt
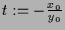 .
.
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-4-05b}\egroup](img2039.png)
-
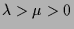 oder
oder
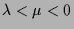 . Dies ist z.B. für
. Dies ist z.B. für  ,
, 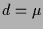 ,
, 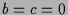 der Fall. Die Lösungen
der Fall. Die Lösungen
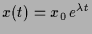 ,
,
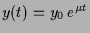 beschreiben halbe verallgemeinerte Parabeln
beschreiben halbe verallgemeinerte Parabeln
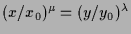 die tangential an
die tangential an  liegen.
liegen.
![\bgroup\color{demo}\includegraphics[scale=1]{pic-4-05c}\egroup](img2040.png)
-
 . Wie zuvor sind die Lösungen
. Wie zuvor sind die Lösungen
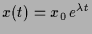 und
und
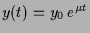 und wegen
und wegen
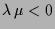 beschreiben diese verallgemeinerte Hyperbeln
beschreiben diese verallgemeinerte Hyperbeln
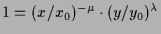 .
.
![\bgroup\color{demo}\includegraphics[scale=.4]{pic-4-05d}\egroup](img2041.png)
-
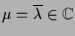 und
und
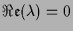 .
Dies ist z.B. für
.
Dies ist z.B. für  ,
, 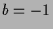 ,
,  der Fall, also für die
Differentialgleichung
der Fall, also für die
Differentialgleichung
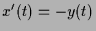 ,
,
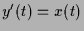 . Damit ist
. Damit ist
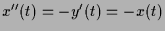 und somit
und somit
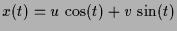 und
und
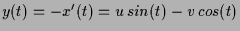 .
Dann ist
.
Dann ist
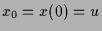 und
und
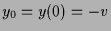 .
Sei nun
.
Sei nun
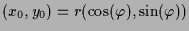 , dann ist
, dann ist
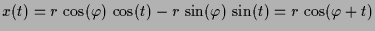 und
und
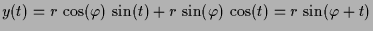 .
Die Lösungen parametrisieren also konzentrische Kreis um 0.
Mittels der komplexen Lösungen
.
Die Lösungen parametrisieren also konzentrische Kreis um 0.
Mittels der komplexen Lösungen
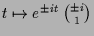 können wir das ebenfalls erhalten indem wir deren Summe
können wir das ebenfalls erhalten indem wir deren Summe
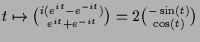 bzw.
das
bzw.
das 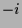 -fache der Differenz
-fache der Differenz
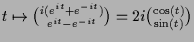 betrachten.
betrachten.
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-4-05e}\egroup](img2042.png)
-
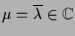 und
und
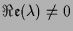 .
Dies ist z.B. für
.
Dies ist z.B. für  und
und 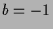 der Fall mit Eigenwerten
der Fall mit Eigenwerten
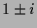 . Komplexe Eigenvektoren sind
. Komplexe Eigenvektoren sind 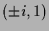 also sind
also sind
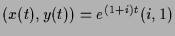 und
und
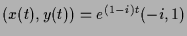 zwei komplexe Lösungen.
Die Summe dieser Lösungen liefert
zwei komplexe Lösungen.
Die Summe dieser Lösungen liefert
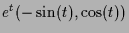 und die Differenz
und die Differenz
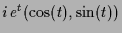 .
Also ist die reelle Lösung mit Anfangswert
.
Also ist die reelle Lösung mit Anfangswert
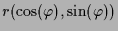 durch
durch
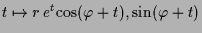 gegeben, parametrisiert
somit eine Spirale die für
gegeben, parametrisiert
somit eine Spirale die für
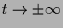 gegen 0 bzw.
gegen 0 bzw.  konvergiert
und dabei unendlich oft um 0 herumläuft.
konvergiert
und dabei unendlich oft um 0 herumläuft.
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-4-05f}\egroup](img2043.png)
- Ist
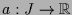 beliebig, dann folgt aus
beliebig, dann folgt aus
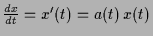 formal
formal
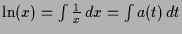 und somit
Einsetzen zeigt, daß dies in der Tat die Lösung der Differentialgleichung ist.
und somit
Einsetzen zeigt, daß dies in der Tat die Lösung der Differentialgleichung ist.
- Ist
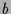 beliebig, so erhält man die Lösung
beliebig, so erhält man die Lösung 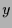 der inhomogenen Gleichung
der inhomogenen Gleichung
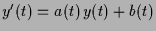 durch Variation der Konstanten der Lösung
durch Variation der Konstanten der Lösung 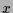 der homogenen Gleichung
der homogenen Gleichung
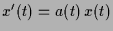 , d.h.
, d.h.
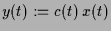 .
Dann ist
.
Dann ist
also
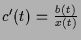 , d.h.
, d.h.
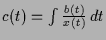 .
.
- Ist
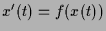 eine Zeit-unabhängige Differentialgleichung
und
eine Zeit-unabhängige Differentialgleichung
und 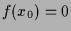 , so ist
, so ist
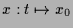 eine stationäre Lösung ein sogenannter Fixpunkt.
Indem man die Ableitung
eine stationäre Lösung ein sogenannter Fixpunkt.
Indem man die Ableitung
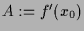 von
von 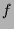 betrachtet, kann man
im generische Fall zeigen, daß sich die Lösungen der Differentialgleichung
betrachtet, kann man
im generische Fall zeigen, daß sich die Lösungen der Differentialgleichung
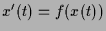 nahe
nahe  im wesentlichen so wie jene der linearen
Differentialgleichung
im wesentlichen so wie jene der linearen
Differentialgleichung
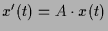 verhalten.
verhalten.
Folgerung.
Das Theorem 4.4.3 gilt auch
für Zeit-abhängige Differential-Gleichungen mit allgemeiner
Anfangsbedingung
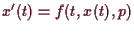
und
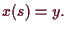
Beweis.
Es sei
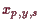 eine Lösung von
eine Lösung von
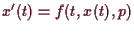
und
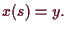
Wir betrachten für
die Differential-Gleichung
mit Anfangswert
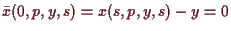 .
Also ist das Problem auf eine Zeit-abhängige
Gleichung mit spezieller Anfangsbedingung
.
Also ist das Problem auf eine Zeit-abhängige
Gleichung mit spezieller Anfangsbedingung
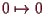 und Parameter
und Parameter
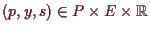 reduziert.
[]
reduziert.
[]
4.4.9 Bemerkung. Differentialgleichungen höherer Ordnung.
Unter einer Differentialgleichung
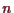 -ter Ordnung versteht man eine
Gleichung der Form
-ter Ordnung versteht man eine
Gleichung der Form
wobei
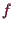 eine lokal definierte Abbildung
eine lokal definierte Abbildung
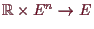 ist und
die Lösung
ist und
die Lösung
 lokal
lokal
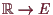
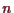 -mal differenzierbar sein soll.
-mal differenzierbar sein soll.
Wenn man
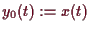 ,
,
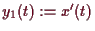 , ...,
, ...,
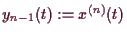 für eine Lösung
für eine Lösung
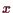 setzt. Dann ist
setzt. Dann ist
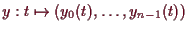 eine Lösung der gewöhnlichen
Differentialgleichung 1. Ordnung:
eine Lösung der gewöhnlichen
Differentialgleichung 1. Ordnung:
wobei
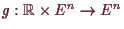 gegeben ist durch
Umgekehrt liefert auch jede Lösung
gegeben ist durch
Umgekehrt liefert auch jede Lösung
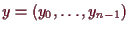 von
von
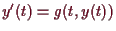 eine Lösung
eine Lösung
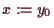 von
von
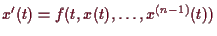 .
.
Ist insbesonders
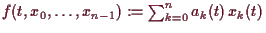 , so ist
, so ist
 linear in
linear in
 und wird durch die Matrix
und wird durch die Matrix
gegeben.
Deren Eigenwerte
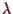 sind gerade
die Lösungen der Gleichung
und somit durch Entwicklung nach der letzten Zeile
von
sind gerade
die Lösungen der Gleichung
und somit durch Entwicklung nach der letzten Zeile
von
| 0 |
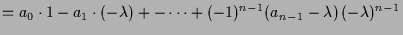 |
|
| |
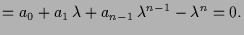 |
|
Andreas Kriegl
2001-07-01
![]() stetig
und bzgl. der zweiten Variable Lipschitz,
wobei
stetig
und bzgl. der zweiten Variable Lipschitz,
wobei
![]() der abgeschlossene Ball im Euklidischen Raum
der abgeschlossene Ball im Euklidischen Raum
![]() mit Mittelpunkt
mit Mittelpunkt
![]() und Radius
und Radius
![]() sei.
Weiters, sei
sei.
Weiters, sei
![]() .
Dann existiert eine eindeutige (iterative erhaltbare) Lösung
.
Dann existiert eine eindeutige (iterative erhaltbare) Lösung
![]() der Differential-Gleichung
der Differential-Gleichung
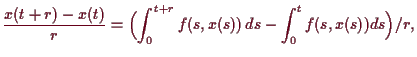
![]() lassen
lassen
![]() invariant, denn für
invariant, denn für
![]() und
und
![]() gilt
gilt
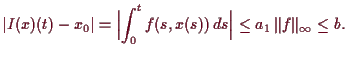
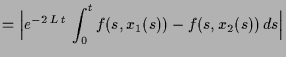
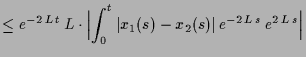
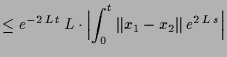
![]() .
Die Lösung
.
Die Lösung
![]() der Differentialgleichung
der Differentialgleichung
![]() mit
Anfangsbedingung
mit
Anfangsbedingung
![]() können wir mittels Separation der Variablen
bestimmen:
können wir mittels Separation der Variablen
bestimmen:

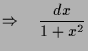
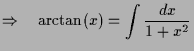
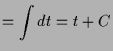
![]() ,
dann existieren die Lösungen dort wo
,
dann existieren die Lösungen dort wo
![]() und
und
![]() stetig sind. []
stetig sind. []

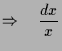
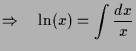
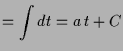
![]() Eigenvektoren von
Eigenvektoren von ![]() mit Eigenwerten
mit Eigenwerten
![]() sind, so ist auch
sind, so ist auch
![]() eine Lösung zum Anfangswert
eine Lösung zum Anfangswert
![]() . Wenn die
. Wenn die ![]() eine Basis bilden, so kann daraus jede
Lösung berechnet werden.
eine Basis bilden, so kann daraus jede
Lösung berechnet werden.
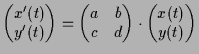
![\bgroup\color{demo}\includegraphics[scale=.3]{pic-4-05a}\egroup](img2038.png)
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-4-05b}\egroup](img2039.png)
![\bgroup\color{demo}\includegraphics[scale=1]{pic-4-05c}\egroup](img2040.png)
![\bgroup\color{demo}\includegraphics[scale=.4]{pic-4-05d}\egroup](img2041.png)
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-4-05e}\egroup](img2042.png)
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-4-05f}\egroup](img2043.png)
![]() -ter Ordnung versteht man eine
Gleichung der Form
-ter Ordnung versteht man eine
Gleichung der Form
![]() ,
,
![]() , ...,
, ...,
![]() für eine Lösung
für eine Lösung
![]() setzt. Dann ist
setzt. Dann ist
![]() eine Lösung der gewöhnlichen
Differentialgleichung 1. Ordnung:
eine Lösung der gewöhnlichen
Differentialgleichung 1. Ordnung:
![]() , so ist
, so ist
![]() linear in
linear in
![]() und wird durch die Matrix
und wird durch die Matrix