Nächste Seite: 5.2 Potenzreihen Aufwärts: 5 Höhere Ableitungen Vorherige Seite: 5 Höhere Ableitungen Inhalt Index
5.1.1 Definition. Zweite Ableitung.
Wir wollen nun die 2. Ableitung einer Funktion
![]() definieren. Natürlich setzen wir voraus, daß
definieren. Natürlich setzen wir voraus, daß
![]() differenzierbar ist. Dann haben wir die Ableitung
differenzierbar ist. Dann haben wir die Ableitung
![]() .
Falls diese ihrerseits differenzierbar ist, so nennen wir
.
Falls diese ihrerseits differenzierbar ist, so nennen wir
![]() 2 mal differenzierbar. Die Ableitung
2 mal differenzierbar. Die Ableitung
![]() von
von
![]() ist dann
eine Abbildung
ist dann
eine Abbildung
![]() .
Wir können aber
.
Wir können aber
![]() mit
mit
![]() nach 3.2.2
identifizieren definieren somit
die 2. Ableitung
nach 3.2.2
identifizieren definieren somit
die 2. Ableitung
![]() von
von
![]() durch
durch
Rekursiv nennen wir
![]() tex2html_wrap_inline$n+1$-mal
(stetig) differenzierbar,
falls
tex2html_wrap_inline$n+1$-mal
(stetig) differenzierbar,
falls
![]()
![]() -mal (stetig)
differenzierbar ist.
Wir schreiben dafür
-mal (stetig)
differenzierbar ist.
Wir schreiben dafür
![]() (
(
![]() ).
Schließlich heißt
).
Schließlich heißt
![]() glatt (kurz
glatt (kurz
![]() ), wenn
), wenn
![]() beliebig oft
differenzierbar ist.
beliebig oft
differenzierbar ist.
Unter der ![]() -ten Ableitung
einer
-ten Ableitung
einer
![]() -mal differenzierbaren Funktion
-mal differenzierbaren Funktion
![]() versteht man
versteht man
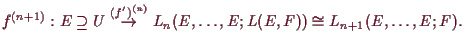
Wir benötigen zuerst den folgenden Spezialfall der Kettenregel für höhere Differenzierbarkeit.
5.1.2 Lemma.
Es sei
![]() linear und
linear und
![]() . Dann ist
. Dann ist
![]() .
.
Beweis. Für
Folglich ist die Differenzierbarkeitsklasse zweier Abbildungen gleich, falls diese auf einen linearen Isomorphismus der Bildräume gleich sind, Wir wollen die Bezeichnung
5.1.3 Lemma.
Beweis. Induktion bezüglich der Differentiationsordnung
![\bgroup\color{demo}$\displaystyle \xymatrix{
E_1\times \dots\times E_n\ar[-0,1] ...
...n\ar[-0,1]_{T\check{}} &L(E_i,F)
\ar[-1,0]_{\operatorname{pr}_i^*} \\
}$\egroup](img2070.png)
Für
![]() erhalten wir die Resultate durch Induktion,
denn wenn
erhalten wir die Resultate durch Induktion,
denn wenn
![]()
![]() ist, so ist
ist, so ist
![]()
![]() .
[]
.
[]
Beachte, daß wir für affine und bilineare Abbildungen (1) direkt zeigen könnten ohne die Kettenregel zu benützen, denn die Ableitung einer bilineare Abbildung ist linear und, die einer linearen Abbildung ist konstant. Jedoch ist die Ableitung eine 3-linearen Abbildung nicht bilinear!
5.1.4 Lemma.
Es sei
![]() und
und
![]() und
und
![]() .
Dann gilt:
.
Dann gilt:
Beweis. Wir zeigen dies durch Induktion nach
Für stetige Differenzierbarkeit haben wir nur zu zeigen, daß
![]() . O.B.d.A. sei
. O.B.d.A. sei
![]() . Dann ist
. Dann ist
![]() wegen
wegen
![]() und daher
und daher
![]() und
und
![]() .
Somit ist
.
Somit ist
![]() , d.h.
, d.h.
![]() .
[]
.
[]
Wir wollen als nächstes 3.3.1 auf höhere Differenzierbarkeit
verallgemeinern, d.h. aus der Existenz der iterierten partiellen Ableitungen
![]() und einer geeigneten Stetigkeitsbedingung
auf
und einer geeigneten Stetigkeitsbedingung
auf
![]() schließen.
schließen.
5.1.5 Proposition.
Es ist
![]()
![]()
![]() alle iterierten partiellen Ableitungen
alle iterierten partiellen Ableitungen
![]() existieren und sind stetig.
Weiters haben wir dann
existieren und sind stetig.
Weiters haben wir dann
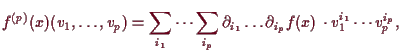
Beweis. Man zeigt dies mittels Induktion wie in 3.3.3. []
5.1.6 Beispiel.
Es sei
![]() gegeben durch
gegeben durch
![]() .
Dann ist
.
Dann ist
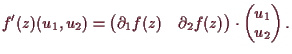
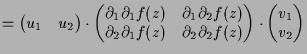 |
Man beachte, daß hier
5.1.7 Schwarz.
Es sei
![]() gegeben. Wir nehmen an,
daß
gegeben. Wir nehmen an,
daß
![]() ,
,
![]() und
und
![]() existieren und stetig in
existieren und stetig in
![]() sind. Dann existiert
sind. Dann existiert
![]() und stimmt überein mit
und stimmt überein mit
![]() .
.
Beweis. Es ist
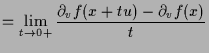 |
||
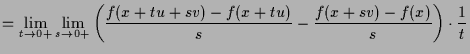 |
||
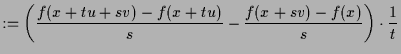 |
||
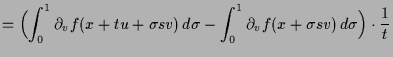 |
||
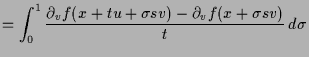 |
||
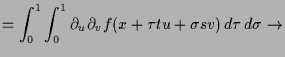 |
||
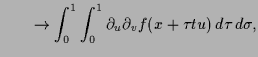 |
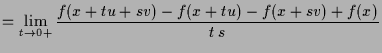 |
||
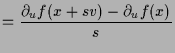 |
Beispiel.
Betrachte

![\bgroup\color{demo}\includegraphics[scale=1]{pic-4-06}\egroup](img2210.png)
Dann existiert
![]() für alle
für alle
![]() , aber
, aber
![]() .
.
In der Tat
![]() ,
,
![]() und daher erhalten wir
und daher erhalten wir
![]() .
Beachte weiters, daß
.
Beachte weiters, daß
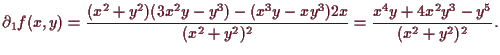
Folgerung.
Es sei
![]()
![]() . Dann ist
. Dann ist
![]() symmetrisch für alle
symmetrisch für alle
![]() .
.
Beweis. Wir zeigen dies mittels Induktion nach
Für
![]() haben wir
haben wir
Bemerkung.
Es sei
![]()
![]() -mal differenzierbar. Dann ist nach
5.1.5
-mal differenzierbar. Dann ist nach
5.1.5
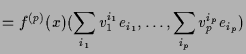 |
||
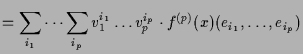 |
||
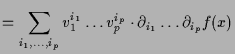 |
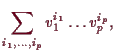
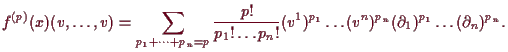
Andreas Kriegl 2001-07-01