Nächste Seite: 5.3 Lokale Extrema Aufwärts: 5 Höhere Ableitungen Vorherige Seite: 5.1 Grundlegendes Inhalt Index
5.2.1 Taylor's Formel.
Es sei
![]()
![]() und
und
![]() .
Dann ist
.
Dann ist
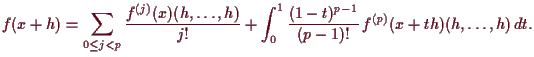
Beweis. Indem wir
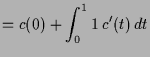 |
||
![$\displaystyle = c(0) + \Bigl[(t-1)\,c'(t)\Bigr]_{t=0}^1 -\int_0^1 (t-1)\,c''(t)\,dt$](img2219.png) |
||
![$\displaystyle = c(0) + c'(0) - \Bigl[\frac{(t-1)^2}{2}\,c''(t)\Bigr]_{t=0}^1 +\int_0^1 \frac{(t-1)^2}{2} \,c'''(t)\,dt$](img2220.png) |
||
![$\displaystyle = c(0) + c'(0) + \dots + \frac1{(p-1)!}\,c^{(p-1)}(0) + \int_0^1 \frac{(1-t)^{p-1}}{(p-1)!}\,c^{(p)}(t)\,dt{\rm\quad[]}$](img2222.png) |
5.2.2 Bemerkung.
Es sei
![]()
![]() . Falls das Restglied
. Falls das Restglied
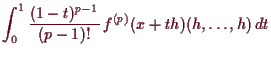
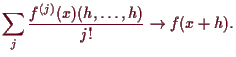
Z.B. ist dies für
![]() ,
,
![]() und
und
![]() der Fall da
der Fall da
![]() ,
,
![]() und
und
![]() .
.
Wir sollten also sogenannte Potenzreihen, d.h.
Reihen der Form
![]() näher untersuchen,
näher untersuchen,
5.2.3 Proposition.
Eine Potenzreihe
![]() konvergiert für
konvergiert für
![]() falls
falls
![]() und divergiert falls
und divergiert falls
![]() , wobei
, wobei
![]() Konvergenzradius der Reihe heißt.
Entsprechend heißt
Konvergenzradius der Reihe heißt.
Entsprechend heißt
![]() Konvergenzkreis der Reihe.
Konvergenzkreis der Reihe.
Dabei dürfen sowohl die Koeffizienten
Beweis. Nach dem Wurzelkriterium genügt es den Ausdruck
5.2.4 Definition. Konvergenz von Funktionen.
Es sei
![]() eine Menge,
eine Menge,
![]() ein endlich dimensionaler Euklidischer Raum
und
ein endlich dimensionaler Euklidischer Raum
und
![]() Funktionen.
Man sagt
Funktionen.
Man sagt
![]() konvergiert gegen
konvergiert gegen
![]() punktweise, wenn
punktweise, wenn
Wenn wir die Abstandsfunktion
![]() auf der Menge
der beschränkten Funktionen
auf der Menge
der beschränkten Funktionen
![]() betrachten, so ist die gleichmäßige
Konvergenz gerade die Konvergenz bezüglich dieser Metrik. Für die punktweise
Konvergenz existiert nur für endliches
betrachten, so ist die gleichmäßige
Konvergenz gerade die Konvergenz bezüglich dieser Metrik. Für die punktweise
Konvergenz existiert nur für endliches
![]() eine sie beschreibende Metrik.
Wenn man
eine sie beschreibende Metrik.
Wenn man
![]() setzt, so ist
setzt, so ist
![]() .
.
5.2.5 Proposition.
Es konvergiere
![]() gleichmäßig auf
gleichmäßig auf
![]() und alle
und alle
![]() seien stetig. Dann ist auch
seien stetig. Dann ist auch
![]() stetig.
In dieser Situation gilt also
stetig.
In dieser Situation gilt also
Beweis. Es sei
5.2.6
Cauchy'sches Konvergenzkriterium für Funktionen.
Es konvergiert
![]() genau dann punktweise, wenn für alle
genau dann punktweise, wenn für alle
![]() die Folge
die Folge
![]() eine Cauchy-Folge ist.
eine Cauchy-Folge ist.
Weiters konvergiert
![]() genau dann gleichmäßig, wenn
genau dann gleichmäßig, wenn
5.2.7
Kriterium von Weierstrass für gleichmäßige Konvergenz.
Es konvergiere
![]() . Dann konvergiert
. Dann konvergiert
![]() gleichmäßig.
gleichmäßig.
Beweis. Es ist
5.2.8 Proposition. Stetigkeit des Integrals.
Es sei
![]() Riemann-integrierbar und
Riemann-integrierbar und
![]() konvergiere
gegen
konvergiere
gegen
![]() gleichmäßig. Dann ist auch
gleichmäßig. Dann ist auch
![]() Riemann-integrierbar
und es gilt
Riemann-integrierbar
und es gilt
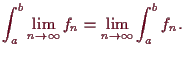
Beweis. Nach dem Lebesgue'schen Integrabilitätskriterium 4.1.4 ist
5.2.9 Proposition.
Es sei
![]() differenzierbar,
differenzierbar,
![]() konvergiere gegen
konvergiere gegen
![]() punktweise und
punktweise und
![]() konvergiere gleichmäßig gegen gegen eine Funktion
konvergiere gleichmäßig gegen gegen eine Funktion
![]() .
Dann ist
.
Dann ist
![]() differenzierbar und die Ableitung
ist
differenzierbar und die Ableitung
ist
![]() , d.h.
es gilt
, d.h.
es gilt
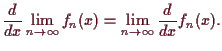
Beweis. Es ist
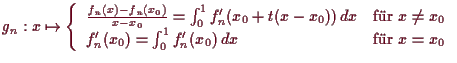
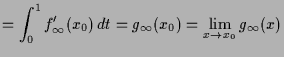 |
||
![$\displaystyle =\lim_{x\to x_0}\frac{f_{\infty}(x)-f_{\infty}(x_0)}{x-x_0} =(f_{\infty})'(x_0).{\rm\quad[]}$](img2283.png) |
5.2.10 Theorem.
Potenzreihen konvergieren auf jedem im Inneren des
Konvergenzkreises enthaltenen Kreisschreibe
gleichmäßig. Sie stellen dort
unendlich oft differenzierbare Abbildungen dar. Die Ableitungen und auch das unbestimmte Integral
können gliedweise
berechnet werden, d.h.
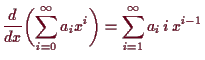 und
und 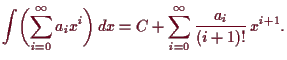
Beweis. Es sei
Man zeigt nun nacheinander, daß
![]() stetig ist bei 0, daß für
stetig ist bei 0, daß für
![]() auch
auch
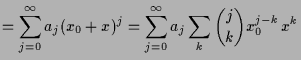 |
||
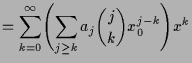 |
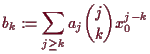
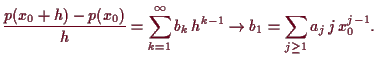
Nach 1.3.6 sind Summen konvergenter Reihen konvergent und nach 1.5.17 Produkte absolut konvergenter Reihen.
Sei nun
![]() mit
mit
![]() und
und
![]() .
Man kann zeigen, daß
.
Man kann zeigen, daß
![]() in eine Potenzreihe entwickeln läßt, die für
in eine Potenzreihe entwickeln läßt, die für
![]() mit
mit
![]() kleiner als der Konvergenzradius von
kleiner als der Konvergenzradius von
![]() und
und
![]() kleiner als der Konvergenzradius von
kleiner als der Konvergenzradius von
![]() auch konvergiert,
auch konvergiert,
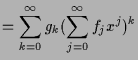 |
||
Da
![]() , wobei
, wobei
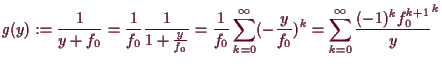
Wegen dem inversen Funktionensatz ist die Summenfunktion
![]() einer
konvergenten Potenzreihe lokal invertierbar, falls
einer
konvergenten Potenzreihe lokal invertierbar, falls
![]() ist.
Wegen
ist.
Wegen
![]() kann man
kann man
![]() ebenfalls in eine Reihe entwickeln.
[]
ebenfalls in eine Reihe entwickeln.
[]
Beispiele.
Es sei
![]() . Dann ist
. Dann ist
![]() und somit nach (gliedweiser) Integration
und somit nach (gliedweiser) Integration
![]() . Wegen
. Wegen
![]() ist
ist
![]() , d.h.
, d.h.
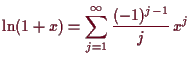 für
für 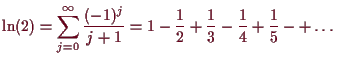
Lemma.
Es sei
![]() eine Potenzreihe mit Konvergenzradius
eine Potenzreihe mit Konvergenzradius
![]() .
Falls eine Folge
.
Falls eine Folge
![]() existiert mit
existiert mit
![]() , dann ist
, dann ist
![]() .
.
Beweis. Wir zeigen mittels Induktion, daß
5.2.11 Beispiel.
Es ist
![]() .
Und
.
Und
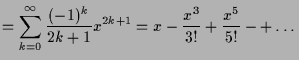 |
||
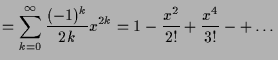 |
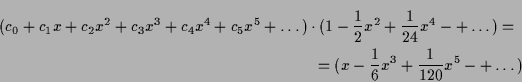
5.2.12 Beispiel.
Es sei
![]() . Dann ist
. Dann ist
![]() ,
also ist die Taylorreihe
,
also ist die Taylorreihe
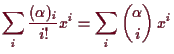
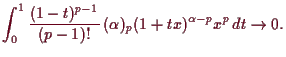
5.2.13 Bemerkung. Komplexe Differenzierbarkeit.
Für Abbildungen
![]() haben wir auch
die Möglichkeit eine Ableitung
haben wir auch
die Möglichkeit eine Ableitung
![]() analog zum 1-dimensionalen reellen Fall zu definieren:
analog zum 1-dimensionalen reellen Fall zu definieren:
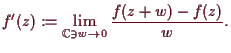
Was ist nun der Zusammenhang zu der linearen Approximation
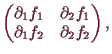
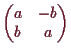
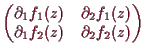
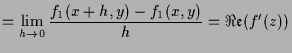 |
||
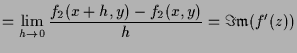 |
||
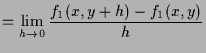 |
||
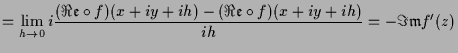 |
||
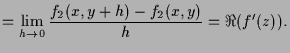 |
Man kann umgekehrt zeigen, daß jedes reell-differenzierbare
![]() welches
die Cauchy-Riemann'schen Differentialgleichungen erfüllt komplex
differenzierbar ist.
welches
die Cauchy-Riemann'schen Differentialgleichungen erfüllt komplex
differenzierbar ist.
Weiters läßt sich jede komplex differenzierbare Abbildung
![]() auf jeder Kreisscheibe in
auf jeder Kreisscheibe in
![]() in eine konvergente Potenzreihe entwickeln und ist somit
insbesonders unendlich oft
(komplex) differenzierbar.
in eine konvergente Potenzreihe entwickeln und ist somit
insbesonders unendlich oft
(komplex) differenzierbar.
5.2.14 Theorem. Glatte Lösungen von Gleichungen.
Folgende Sätze gelten auch für
![]() -mal stetig differenzierbare und auch
für glatte Abbildungen:
-mal stetig differenzierbare und auch
für glatte Abbildungen:
Beweis. Wir zeigen dies mittels Induktion nach
(4) Beachte, daß wir für
![]() erhalten haben, daß
erhalten haben, daß
![]() .
Wobei
.
Wobei
![]() stetig und linear ist. Also folgt mittels Induktion, daß
stetig und linear ist. Also folgt mittels Induktion, daß
![]()
![]() ist und damit auch
ist und damit auch
![]() , also
, also
![]()
![]() ist.
ist.
(5) Im Beweis für
![]() , haben wir ein implizite
Lösung
, haben wir ein implizite
Lösung
![]() erhalten. Diese ist
nun nach (4) und (2) auch
erhalten. Diese ist
nun nach (4) und (2) auch
![]() , also ist
, also ist
![]() in
in
![]()
![]() und der
Definitionsbereich hat sich nicht verkleinert.
und der
Definitionsbereich hat sich nicht verkleinert.
Für zeitabhängige Differentialgleichungen mit einer allgemeinen
Anfangsbedingung
folgt das nun ebenso wie im
![]() -Fall.
[]
-Fall.
[]
Andreas Kriegl 2001-07-01