5.3.1 Definition.
Es sei
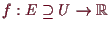 und
und
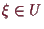 .
Dann heißt
.
Dann heißt
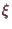 lokales Maximum (resp. Minimum) von
lokales Maximum (resp. Minimum) von
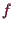 , genau dann
wenn ein
, genau dann
wenn ein
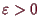 existiert, so daß für all
existiert, so daß für all
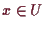 mit
mit
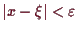 die Ungleichung
die Ungleichung
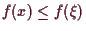 (resp.
(resp.
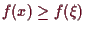 )
gilt. Gilt sogar die strikte Ungleichung
)
gilt. Gilt sogar die strikte Ungleichung
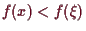 (resp.
(resp.
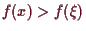 ) für all jene
) für all jene
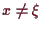 , so heißt
, so heißt
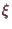 ein lokales striktes
Maximum (resp. Minimum).
ein lokales striktes
Maximum (resp. Minimum).
5.3.2 Lemma.
Es sei
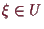 ein lokales Extremum (d.h. Maximum oder Minimum) von
ein lokales Extremum (d.h. Maximum oder Minimum) von
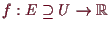 und
und
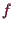 sei differenzierbar bei
sei differenzierbar bei
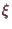 oder besitze
zumindest die Richtungsableitungen
oder besitze
zumindest die Richtungsableitungen
 für alle
für alle
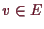 .
.
Dann ist
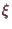 ein kritischer Punkt von
ein kritischer Punkt von
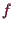 , d.h.
, d.h.
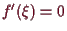 .
.
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-5-02}\egroup](img2538.png)
Beweis.
Für
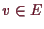 besitzt auch
besitzt auch
 ein lokales Extremum bei
ein lokales Extremum bei
 und somit z.B. im Falle eines lokalen Minimums
und somit z.B. im Falle eines lokalen Minimums
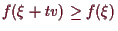 für alle
für alle
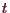 und damit
also ist
und damit
also ist
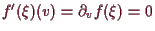 .
[]
.
[]
5.3.3 Proposition (lokale Extrema).
Es sei
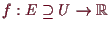
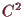 ,
,
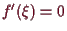 und die symmetrische Form
und die symmetrische Form
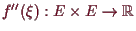 sei positiv definit. Dann hat
sei positiv definit. Dann hat
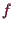 bei
bei
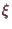 ein striktes lokales Minimum.
ein striktes lokales Minimum.
Eine bilineare symmetrische Form
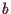 ist genau dann positiv definit,
wenn
ist genau dann positiv definit,
wenn
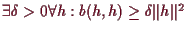 :
Denn die Einheitssphäre
:
Denn die Einheitssphäre
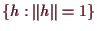 ist kompakt und somit
existiert
ist kompakt und somit
existiert
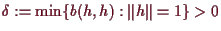 und für
und für
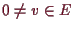 gilt
gilt
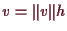 , wobei
, wobei
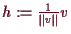 und damit
und damit
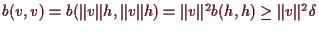 .
.
In der Mathematik 1 haben wir gezeigt, daß
eine bilinear-Form
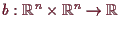 genau dann positiv
definit ist, wenn es die zugehörige quadratische Matrix
genau dann positiv
definit ist, wenn es die zugehörige quadratische Matrix
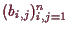 mit
mit
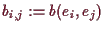 ist, d.h.
die Determinante der Hauptminore
ist, d.h.
die Determinante der Hauptminore
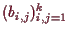 positiv ist für jedes
positiv ist für jedes
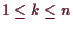 .
.
Beweis.
O.B.d.A. sei
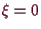 . Nach Taylor's Theorem 5.2.1 ist
Die Menge der stetigen positiv definiten symmetrischen Bilinear-Formen
ist offen in allen symmetrischen Bilinear-Formen, denn wenn
. Nach Taylor's Theorem 5.2.1 ist
Die Menge der stetigen positiv definiten symmetrischen Bilinear-Formen
ist offen in allen symmetrischen Bilinear-Formen, denn wenn
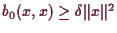 ist und
ist und
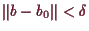 ist, so ist
ist, so ist
Da
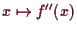 stetig ist und
stetig ist und
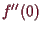 positiv definit ist existiert
ein
positiv definit ist existiert
ein
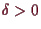 und ein
und ein
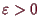 , so daß alle
, so daß alle
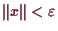 in
in
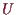 liegen und
liegen und
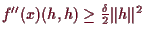 für alle
für alle
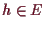 gilt.
Somit ist für diese
gilt.
Somit ist für diese
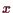 daher ist
daher ist
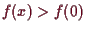 für alle
für alle
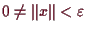 .
[]
.
[]
5.3.4 Beispiele.
-
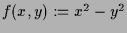 hat nur
hat nur 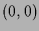 als kritischen Punkt. Dieser ist
ein Sattelpunkt.
als kritischen Punkt. Dieser ist
ein Sattelpunkt.
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-5-03}\egroup](img2539.png)
-
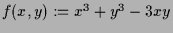 hat nur
hat nur 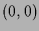 und
und 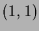 als kritische
Punkte. Der erste ist ein Sattelpunkt (setze
als kritische
Punkte. Der erste ist ein Sattelpunkt (setze 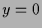 ) und der zweite ein
lokales striktes Minimum.
) und der zweite ein
lokales striktes Minimum.
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-5-04}\egroup](img2540.png)
-
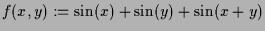 für
für
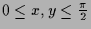 .
.
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-5-05}\egroup](img2541.png)
Der einzige kritische Punkt im Inneren ist
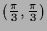 ,
ein globales Maximum. Am Rand sind
,
ein globales Maximum. Am Rand sind 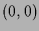 und
und
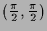 lokale Minima und
lokale Minima und
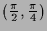 und
und
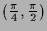 lokale
Maxima, davon ist der erste Punkt ist ein globales Minimum von
lokale
Maxima, davon ist der erste Punkt ist ein globales Minimum von 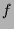 ,
und die beiden anderen Sattelpunkte.
,
und die beiden anderen Sattelpunkte.
5.3.5 Proposition über Lagrange Multiplikatoren.
Es sei
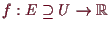 und
und
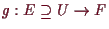 , beide
, beide
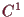 . Falls
. Falls
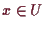 ein lokales Extremum von
ein lokales Extremum von
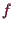 mit der Nebenbedingung
mit der Nebenbedingung
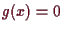 ist und falls
ist und falls
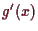 surjektiv ist, so
ist
surjektiv ist, so
ist
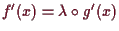 für ein
für ein
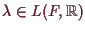 .
.
Beweis.
O.B.d.A. sei
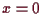 .
Es sei
.
Es sei
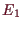 der Kern von
der Kern von
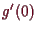 und
und
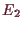 ein Komplementärraum zu
ein Komplementärraum zu
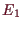 also
z.B. das orthogonale Komplement
also
z.B. das orthogonale Komplement
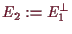 .
Dann ist
.
Dann ist
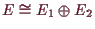 und wir bezeichnen mit
und wir bezeichnen mit
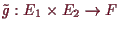 die Abbildung
die Abbildung
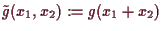 und analog
und analog
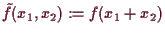 . Dann ist
. Dann ist
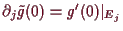 und insbesonders ist
und insbesonders ist
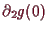 injektiv, da
injektiv, da
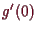 nur
auf
nur
auf
 verschwindet, und ebenso surjektiv, denn aus
verschwindet, und ebenso surjektiv, denn aus
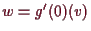 folgt für
folgt für
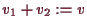 die Gleichung
die Gleichung
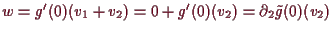 (Man sieht auch leicht, daß
(Man sieht auch leicht, daß
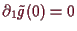 ).
Aus dem Satz über implizite Abbildungen folgt die Existenz einer
lokal eindeutigen
).
Aus dem Satz über implizite Abbildungen folgt die Existenz einer
lokal eindeutigen
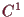 -Lösung
-Lösung
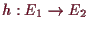 der impliziten Gleichung
der impliziten Gleichung
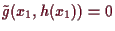 , d.h.
, d.h.
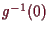 läßt sich
lokal durch den Graph einer Abbildung
läßt sich
lokal durch den Graph einer Abbildung
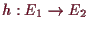 parametrisieren läßt. Damit ist das Extremalproblem für
parametrisieren läßt. Damit ist das Extremalproblem für
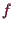 mit
Nebenbedingung
mit
Nebenbedingung
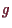 auf das gewöhnliche Extremalproblem für
auf das gewöhnliche Extremalproblem für
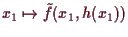 ohne Nebenbedingung zurückgeführt.
Da
ohne Nebenbedingung zurückgeführt.
Da
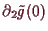 invertierbar ist können wir
invertierbar ist können wir
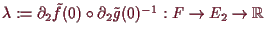 setzen, und erhalten
setzen, und erhalten
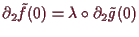 Nach 5.3.3 die Ableitung
Nach 5.3.3 die Ableitung
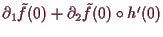 von
von
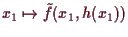 bei 0 verschwinden.
Ebenso folgt durch Differenzieren von
bei 0 verschwinden.
Ebenso folgt durch Differenzieren von
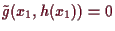 ,
daß die
Ableitung
,
daß die
Ableitung
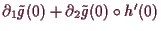 verschwindet, und da
verschwindet, und da
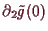 invertierbar ist,
ist
invertierbar ist,
ist
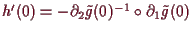 (Wegen
(Wegen
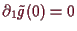 ist
ist
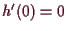 ).
Somit ist
).
Somit ist
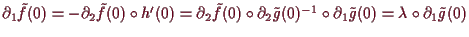 (Und dies ist 0).
Also ist insgesamt
(Und dies ist 0).
Also ist insgesamt
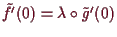 ,
und somit auch
,
und somit auch
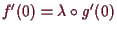 , da
, da
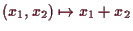 ein linearer Isomorphismus
ein linearer Isomorphismus
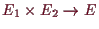 ist der
ist der
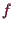 und
und
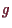 in
in
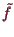 und
und
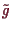 übersetzt.
[]
übersetzt.
[]
Wenn
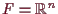 ist, dann ist
ist, dann ist
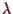 durch
durch
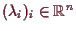 vermöge
vermöge
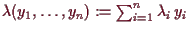 gegeben und
somit muß ein relatives lokales Extremum
gegeben und
somit muß ein relatives lokales Extremum
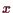 folgendes
erfüllen
folgendes
erfüllen
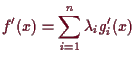
und
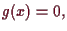
wobei
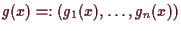 ist.
Ist zusätzlich
ist.
Ist zusätzlich
 so bedeutet dies für ein lokales Extremum
so bedeutet dies für ein lokales Extremum
 folgendes
(im allgemeinen nur bzgl. der
folgendes
(im allgemeinen nur bzgl. der
 lineare) Gleichungssystem von
lineare) Gleichungssystem von
 Gleichungen in den
Gleichungen in den
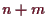 vielen Variablen
vielen Variablen
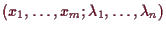 :
:
Da der letzte Satz nur eine notwendige Bedingung liefert, benötigt man
zusätzliche Argumente um den Nachweis eines lokalen Extremums zu liefern.
Das kann z.B. sein, daß die Nebenbedingung eine kompakte Menge beschreibt
und die stetige Funktion
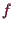 somit ein Maximum und ein Minimum besitzen muß.
somit ein Maximum und ein Minimum besitzen muß.
5.3.7 Beispiele.
- Die Extremalwerte von
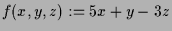 auf dem Durchschnitt der Ebene
auf dem Durchschnitt der Ebene
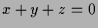 mit der Sphäre
mit der Sphäre
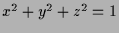 .
Die Abbildung
.
Die Abbildung 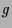 ist in diesem Beispiel
ist in diesem Beispiel
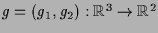 mit
mit
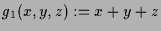 und
und
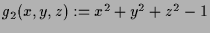 .
Es ist somit folgendes Gleichungssystem im
.
Es ist somit folgendes Gleichungssystem im
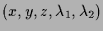 zu lösen:
zu lösen:
Die einzigen Lösungen sind
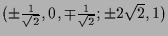 .
Einsetzen in
.
Einsetzen in 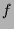 zeigt, daß
zeigt, daß
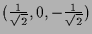 die Stelle eines lokalen (und somit auch globalen) Maximums und
die Stelle eines lokalen (und somit auch globalen) Maximums und
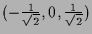 die eines globalen Minimums ist.
die eines globalen Minimums ist.
- Sei
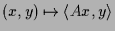 eine bilineare symmetrische Form.
Gesucht sind ihre Extremalwerte unter der Nebenbedingung
eine bilineare symmetrische Form.
Gesucht sind ihre Extremalwerte unter der Nebenbedingung 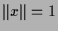 .
Die Methode der Lagrangemultiplikatoren liefert:
.
Die Methode der Lagrangemultiplikatoren liefert:
Wegen der Symmetrie von  also
also
 und
und 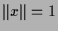 und somit ist
und somit ist  ein normierter Eigenvektor
zum Eigenwert
ein normierter Eigenvektor
zum Eigenwert 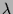 . Ist
. Ist 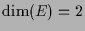 , dann liefert die beiden Eigenwerte
, dann liefert die beiden Eigenwerte
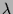 das Maximum und das Minimum. Das sind gerade die Längen
der Halbachsen des Ellipse oder Hyperbel
das Maximum und das Minimum. Das sind gerade die Längen
der Halbachsen des Ellipse oder Hyperbel
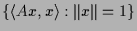 und die
zugehörigen Eigenvektoren sind die Richtungsvektoren der Halbachsen.
und die
zugehörigen Eigenvektoren sind die Richtungsvektoren der Halbachsen.
Andreas Kriegl
2001-07-01
![]() und
und
![]() .
Dann heißt
.
Dann heißt
![]() lokales Maximum (resp. Minimum) von
lokales Maximum (resp. Minimum) von
![]() , genau dann
wenn ein
, genau dann
wenn ein
![]() existiert, so daß für all
existiert, so daß für all
![]() mit
mit
![]() die Ungleichung
die Ungleichung
![]() (resp.
(resp.
![]() )
gilt. Gilt sogar die strikte Ungleichung
)
gilt. Gilt sogar die strikte Ungleichung
![]() (resp.
(resp.
![]() ) für all jene
) für all jene
![]() , so heißt
, so heißt
![]() ein lokales striktes
Maximum (resp. Minimum).
ein lokales striktes
Maximum (resp. Minimum).
![]() ein lokales Extremum (d.h. Maximum oder Minimum) von
ein lokales Extremum (d.h. Maximum oder Minimum) von
![]() und
und
![]() sei differenzierbar bei
sei differenzierbar bei
![]() oder besitze
zumindest die Richtungsableitungen
oder besitze
zumindest die Richtungsableitungen
![]() für alle
für alle
![]() .
.
![]() ein kritischer Punkt von
ein kritischer Punkt von
![]() , d.h.
, d.h.
![]() .
.
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-5-02}\egroup](img2538.png)
![]()
![]() ,
,
![]() und die symmetrische Form
und die symmetrische Form
![]() sei positiv definit. Dann hat
sei positiv definit. Dann hat
![]() bei
bei
![]() ein striktes lokales Minimum.
ein striktes lokales Minimum.
![]() genau dann positiv
definit ist, wenn es die zugehörige quadratische Matrix
genau dann positiv
definit ist, wenn es die zugehörige quadratische Matrix
![]() mit
mit
![]() ist, d.h.
die Determinante der Hauptminore
ist, d.h.
die Determinante der Hauptminore
![]() positiv ist für jedes
positiv ist für jedes
![]() .
.
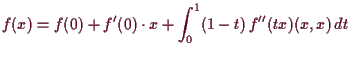
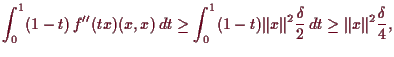
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-5-03}\egroup](img2539.png)
![\bgroup\color{demo}\includegraphics[scale=.7]{pic-5-04}\egroup](img2540.png)
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-5-05}\egroup](img2541.png)
![]() ,
ein globales Maximum. Am Rand sind
,
ein globales Maximum. Am Rand sind ![]() und
und
![]() lokale Minima und
lokale Minima und
![]() und
und
![]() lokale
Maxima, davon ist der erste Punkt ist ein globales Minimum von
lokale
Maxima, davon ist der erste Punkt ist ein globales Minimum von ![]() ,
und die beiden anderen Sattelpunkte.
,
und die beiden anderen Sattelpunkte.
![]() und
und
![]() , beide
, beide
![]() . Falls
. Falls
![]() ein lokales Extremum von
ein lokales Extremum von
![]() mit der Nebenbedingung
mit der Nebenbedingung
![]() ist und falls
ist und falls
![]() surjektiv ist, so
ist
surjektiv ist, so
ist
![]() für ein
für ein
![]() .
.
![]() ist, dann ist
ist, dann ist
![]() durch
durch
![]() vermöge
vermöge
![]() gegeben und
somit muß ein relatives lokales Extremum
gegeben und
somit muß ein relatives lokales Extremum
![]() folgendes
erfüllen
folgendes
erfüllen
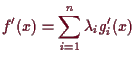 und
und 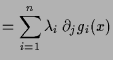 für
für ![]() somit ein Maximum und ein Minimum besitzen muß.
somit ein Maximum und ein Minimum besitzen muß.