Nächste Seite: 6.3 Integrationsmethoden Aufwärts: 6 Mehrfach Integrale Vorherige Seite: 6.1 Integration über Intervalle Inhalt Index
6.2.1 Definition.
Es sei
![]() beschränkt.
Dann heißt
beschränkt.
Dann heißt
![]() Riemann-integrierbar (auf
Riemann-integrierbar (auf
![]() )
)
![]() für ein (alle) kompaktes mehrdimensionales
Intervall
für ein (alle) kompaktes mehrdimensionales
Intervall
![]() ist die Fortsetzung
ist die Fortsetzung
![]() von
von
![]() , die
durch
, die
durch
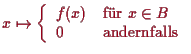
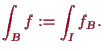
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-6-02}\egroup](img2721.png)
Eine beschränkte Menge
![]() heißt Jordan-meßbar
heißt Jordan-meßbar
![]() die konstante Funktion
die konstante Funktion
![]() ist Riemann-integrierbar über
ist Riemann-integrierbar über
![]() , d.h. die charakteristische Funktion
, d.h. die charakteristische Funktion
![]() ist Riemann-integrierbar über ein/jedes kompakte
Intervall, welches
ist Riemann-integrierbar über ein/jedes kompakte
Intervall, welches
![]() enthält.
Das Volumen oder auch Maß
einer
enthält.
Das Volumen oder auch Maß
einer
![]() -meßbaren Menge definiert man als
-meßbaren Menge definiert man als
![]() .
.
6.2.2 Proposition.
Eine Teilmenge
![]() ist genau dann
ist genau dann
![]() -meßbar, wenn
-meßbar, wenn
![]() beschränkt und der Rand
beschränkt und der Rand
![]() von
von
![]() eine Lebesgue-Nullmenge ist.
eine Lebesgue-Nullmenge ist.
Unter dem Rand
Beweis.
6.2.3 Folgerung.
Es seien
![]() und
und
![]()
![]() -meßbar. Dann sind auch
-meßbar. Dann sind auch
![]() ,
,
![]() und
und
![]()
![]() -meßbar.
-meßbar.
Beweis. Es ist
6.2.4 Lebesgue'sches Integrabilitätskriterium.
Es sei
![]()
![]() -meßbar. Dann ist eine beschränkte Funktion
-meßbar. Dann ist eine beschränkte Funktion
![]() genau dann
genau dann
![]() -integrierbar,
falls
-integrierbar,
falls
![]() fast überall stetig auf
fast überall stetig auf
![]() ist.
ist.
Beweis. Es sei
6.2.5 Folgerung.
Es sei
![]()
![]() -meßbar und
-meßbar und
![]() und
und
![]()
![]() -integrierbar auf
-integrierbar auf
![]() und
und
![]() .
Dann ist
.
Dann ist
![]()
![]() -integrierbar auf
-integrierbar auf
![]() und
und
![]() . Weiters sind
. Weiters sind
![]() ,
,
![]() ,
,
![]() und
und
![]() allesamt
allesamt
![]() -integrierbar auf
-integrierbar auf
![]() .
.
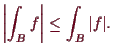
6.2.6 Mittelwertsatz.
Es sei
![]()
![]() -meßbar und
-meßbar und
![]()
![]() -integrierbar auf
-integrierbar auf
![]() .
Dann ist
.
Dann ist
![\bgroup\color{proclaim}$\displaystyle \vert B\vert\, \inf(f(B)) \leq \int_B f \leq \vert B\vert\, \sup(f(B)).{\rm\quad[]}
$\egroup](img2689.png)
6.2.7 Folgerung.
Es sei
![]() eine
eine
![]() -Nullmenge, d.h.
-Nullmenge, d.h.
![]() ist
ist
![]() -meßbar und
-meßbar und
![]() .
Dann ist jede beschränkte Funktion
.
Dann ist jede beschränkte Funktion
![]()
![]() -integrierbar
mit
-integrierbar
mit
![]() .
.
Beweis. Wegen
6.2.8 Proposition.
![]()
![]() -meßbar
-meßbar
![]()
![]() ist beschränkt und
ist beschränkt und
![]() ist
ist
![]() -Nullmenge.
-Nullmenge.
Beweis. Kompakte Mengen sind genau dann Lebesgue-Nullmengen, wenn sie Jordan-Nullmengen sind. Sei nämlich
6.2.9 Folgerung.
![]()
![]() -integrierbar,
-integrierbar,
![]() beide
beide
![]() -meßbar
-meßbar
![]()
![]()
![]() -integrierbar. []
-integrierbar. []
6.2.10 Proposition.
Es sei
![]()
![]() -integrierbar auf den
-integrierbar auf den
![]() -meßbaren Mengen
-meßbaren Mengen
![]() und
und
![]() .
Dann ist
.
Dann ist
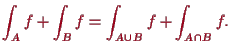
Beweis. 6.2.3
Wegen
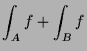 |
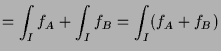 |
|
![$\displaystyle = \int_I (f_{A\cup B}+f_{A\cap B}) =\int_I f_{A\cup B}+ \int_I f_{A\cap B} = \int_{A\cup B} f + \int_{A\cap B} f.{\rm\quad[]}$](img2717.png) |
6.2.11 Folgerung.
Es seien
![]() ,
,
![]()
![]() -meßbar
-meßbar
![]()
![]() .
.
![]()
![]()
![]() . []
. []
Andreas Kriegl 2001-07-01