Nächste Seite: 6.4 Kurven-Integrale Aufwärts: 6 Mehrfach Integrale Vorherige Seite: 6.2 Integration über meßbare Inhalt Index
6.3.1 Proposition.
![]()
![]() -meßbar,
-meßbar,
![]()
![]() -integrierbar
-integrierbar
![]()
![]() ist
ist
![]() -Nullmenge in
-Nullmenge in
![]() .
.
Beweis. Es sei
6.3.2 Folgerung.
![]()
![]() -meßbar,
-meßbar,
![]()
![]() -integrierbar,
-integrierbar,
![]()
![]() Die Ordinatenmenge
Die Ordinatenmenge
![]() mit Grenzen
mit Grenzen
![]() ist
ist
![]() -meßbar in
-meßbar in
![]() und
und
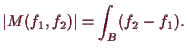
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-6-03}\egroup](img2884.png)
Weiters ist jede stetige und beschränkte Funktion
![]()
![]() -integrierbar
auf
-integrierbar
auf
![]() und
und
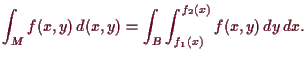
Dies zeigt, daß die Definition 6.2.1 der Fläche als
Beweis.
Es sei
![]() , dann ist
, dann ist
![$\displaystyle = \int_{I\times [\inf f_1,\sup f_2]} f_M \AMSoverset{\text{Fubini}}\to= \int_I \int_{\inf f_1}^{\sup f_2}f_M(x,y)\,dy\,dx$](img2743.png) |
||
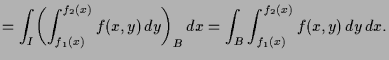 |
![\bgroup\color{demo}$\displaystyle \vert M(f_1,f_2)\vert = \int_M 1
= \int_B \int_{f_1(x)}^{f_2(x)} 1\,dy\,dx= \int_B f_2-f_1. {\rm\quad[]}
$\egroup](img2746.png)
Beispiel.
Die Fläche
![]() einer Kreisscheibe
einer Kreisscheibe
![]() .
.
Für
![]() ,
,
![]() ,
,
![]() ist
ist
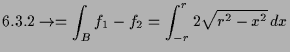 |
||
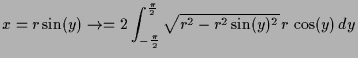 |
||
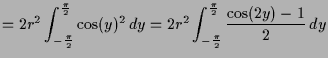 |
||
![$\displaystyle = 2r^2 \left[\frac{\sin(2y)}4-\frac{y}2\right]_{y=-\frac{\pi}2}^{y=\frac\pi2} = r^2 \pi$](img2756.png) |
6.3.3 Formel von Cavaleri.
Es sei
![]()
![]() -meßbar, und für alle
-meßbar, und für alle
![]() sei
sei
![]()
![]() -meßbar.
Dann ist
-meßbar.
Dann ist
![]() auf
auf
![]()
![]() -integrierbar und
-integrierbar und
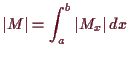
Falls
![\bgroup\color{demo}\includegraphics[scale=.5]{pic-6-04}\egroup](img2885.png)
Das Volumen von
![]() ist somit
ist somit
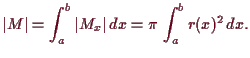
Beweis. Es ist
![$\displaystyle = \int_{[a,b]\times J} \chi _M \AMSoverset{\text{Fubini}}\to = \int_a^b \int_J \chi _M(x,y)\,dy\, dx$](img2768.png) |
||
![$\displaystyle = \int_a^b \int_J \chi _{M_x}(y)\,dy\, dx = \int_a^b \vert M_x\vert\,dx {\rm\quad[]}$](img2769.png) |
Beispiel.
Das Volumen der Kugel
![]() . Es ist
. Es ist
![]()
![]() -meßbar(!) und
-meßbar(!) und
![]() eine Kreisscheibe mit Radius
eine Kreisscheibe mit Radius
![]() und
somit Fläche
und
somit Fläche
![]() . Nach 6.3.3 ist also
. Nach 6.3.3 ist also
![\bgroup\color{demo}$\displaystyle \vert K\vert = \int_{-r}^r \vert K_x\vert\,dx ...
... \pi\Bigl[r^2 x -\frac{x^3}3 \Bigr]_{x=-r}^{x=r} = \frac{4 r^3 \pi}{3}.
$\egroup](img2775.png)
6.3.4 Lemma.
Es sei
![]() eine Lipschitz-Abbildung mit Konstante
eine Lipschitz-Abbildung mit Konstante
![]() . Für jeden (achsenparallelen) Würfel
. Für jeden (achsenparallelen) Würfel
![]() mit Seitenlänge
mit Seitenlänge
![]() der
der
![]() trifft
existiert ein
Würfel
trifft
existiert ein
Würfel
![]() mit
mit
![]() und
und
![]() .
.
Der Fall
Beweis. Es sei
6.3.5 Folgerung.
Lipschitz stetige Bilder von
![]() -Nullmengen sind
-Nullmengen sind
![]() -Nullmengen, d.h.
-Nullmengen, d.h.
![]() ist eine
ist eine
![]() -Nullmenge, falls
-Nullmenge, falls
![]() eine ist und
eine ist und
![]() Lipschitz-stetig ist.
Lipschitz-stetig ist.
Dieses Resultat stimmt auch noch, wenn
Beweis. Es ist
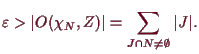
Definition.
Eine Abbildung
![]() auf einer beliebigen Teilmenge
auf einer beliebigen Teilmenge
![]() von
von
![]() heißt
heißt
![]() (stetig differenzierbar)
(stetig differenzierbar)
![]()
![]()
![]() mit
mit
![]() offen.
offen.
6.3.6 Proposition.
Es sei
![]()
![]() und
und
![]() eine kompakte
eine kompakte
![]() -Nullmenge.
Dann ist
-Nullmenge.
Dann ist
![]() eine
eine
![]() -Nullmenge.
-Nullmenge.
Beweis. Wegen 6.3.5 genügt zu zeigen, daß
6.3.7 Satz.
Es sei
![]() kompakt
kompakt
![]() -meßbar und
-meßbar und
![]()
![]() . Es sei
. Es sei
![]() eine
eine
![]() -Nullmenge mit
-Nullmenge mit
![]() invertierbar
für alle
invertierbar
für alle
![]() .
Dann ist
.
Dann ist
![]()
![]() -meßbar.
-meßbar.
Falls
Beweis.
Bemerkung.
Stetige Bilder von Nullmengen sind nicht immer Nullmengen.
6.3.8 Substitutionsregel.
Es sei
![]() ein Quader,
ein Quader,
![]()
![]() und
und
![]() stetig.
Sei weiters eine Zerlegung
stetig.
Sei weiters eine Zerlegung
![]() von
von
![]() vorgegeben. Das Bild eines Teilungsrechtecks
vorgegeben. Das Bild eines Teilungsrechtecks
![]() hat annähernd die Fläche des von
hat annähernd die Fläche des von
![]() und
und
![]() erzeugten Parallelogramms, also
erzeugten Parallelogramms, also
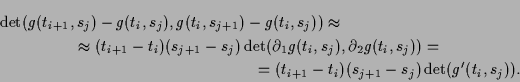
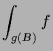 |
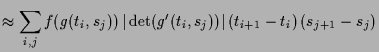 |
|
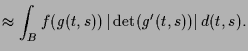 |
Theorem.
![]() kompakt und
kompakt und
![]() -meßbar,
-meßbar,
![]()
![]() ,
,
![]() eine
eine
![]() -Nullmenge,
-Nullmenge,
![]() injektiv,
injektiv,
![]() konstant und nicht 0 auf
konstant und nicht 0 auf
![]() ,
,
![]() stetig.
stetig.
Dann ist
![]()
![]() -meßbar,
-meßbar,
![]()
![]() -integrierbar auf
-integrierbar auf
![]() und
es gilt folgende Transformationsformel
und
es gilt folgende Transformationsformel
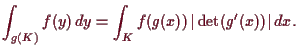
Im Falle
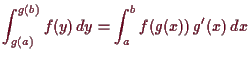

Bemerkung.
Vergleiche die Substitutionsregel
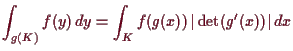
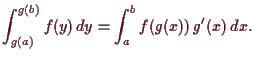
Polarkoordinaten.
Die Transformation von Polar- auf kartesische Koordinaten ist
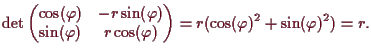
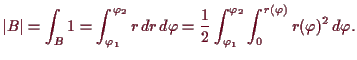
Zylinderkoordinaten.
Die Transformation von Zylinder- auf Kartesische Koordinaten ist
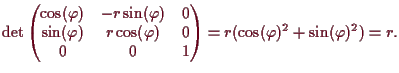
Kugelkoordinaten.
Die Transformation von Kugel- auf Kartesische Koordinaten ist
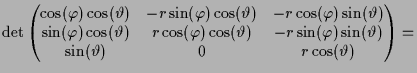 |
||
Andreas Kriegl 2001-07-01