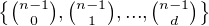 ,
where d = dim P.
Similarly to h/h*-vectors, the f*-vector of P coincides with the f-vector of
its unimodular triangulations (if they exist).
We present several inequalities that hold among the coefficients of f*-vectors of polytopes.
These inequalities resemble striking similarities with existing inequalities for the
coefficients of f-vectors of simplicial polytopes; e.g., the first half of the
f*-coefficients increases and the last quarter decreases.
Even though f*-vectors of polytopes are not always unimodal, there are several families of polytopes that carry the unimodality property.
We also show that for any polytope with a given Ehrhart h*-vector, there is a polytope with the same h*-vector whose f*-vector is unimodal.
,
where d = dim P.
Similarly to h/h*-vectors, the f*-vector of P coincides with the f-vector of
its unimodular triangulations (if they exist).
We present several inequalities that hold among the coefficients of f*-vectors of polytopes.
These inequalities resemble striking similarities with existing inequalities for the
coefficients of f-vectors of simplicial polytopes; e.g., the first half of the
f*-coefficients increases and the last quarter decreases.
Even though f*-vectors of polytopes are not always unimodal, there are several families of polytopes that carry the unimodality property.
We also show that for any polytope with a given Ehrhart h*-vector, there is a polytope with the same h*-vector whose f*-vector is unimodal.
The following versions are available: