Nächste Seite: Index Aufwärts: Mathematik 1 für Informatik Vorherige Seite: 13 Euklid'ische Geometrie Inhalt Index
Wir wollen nun ein geometrischeres Verständnis von linearen Abbildungen
![]() entwickeln.
entwickeln.
14.1 Bemerkung.
Es sei
![]() . Wir wollen eruieren, wo
. Wir wollen eruieren, wo
![]() einfach
als Streckung wirkt, d.h. jene
einfach
als Streckung wirkt, d.h. jene
![]() bestimmen, für welche
bestimmen, für welche
![]() für ein
für ein
![]() ist.
Das homogene Gleichungssystem
ist.
Das homogene Gleichungssystem
![]() hat genau dann eine nichttriviale Lösung
hat genau dann eine nichttriviale Lösung
![]() , wenn
, wenn
![]() ist.
Beachte, daß
ist.
Beachte, daß
![]() ein Polynom vom Grad
ein Polynom vom Grad
![]() ist.
Es heißt das charakteristische Polynom
von
ist.
Es heißt das charakteristische Polynom
von
![]() . Seine Nullstellen heißen Eigenwerte von
. Seine Nullstellen heißen Eigenwerte von
![]() ,
die Menge
,
die Menge
![]() der Lösungen
der Lösungen
![]() von
von
![]() heißt Eigenraum zum Eigenwert
heißt Eigenraum zum Eigenwert
![]() , und dessen Elemente
, und dessen Elemente
![]() heißen Eigenvektoren von
heißen Eigenvektoren von
![]() zum Eigenwert
zum Eigenwert
![]() .
.
14.1a Beispiel.
Wir betrachten die lineare Abbildung
![]()
![]() mit Matrizendarstellung
mit Matrizendarstellung
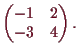
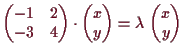
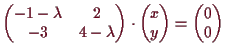
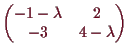
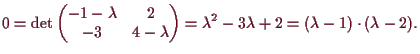
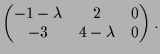 |
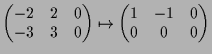 |
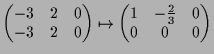 |
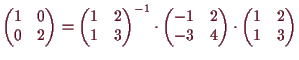
14.2 Proposition.
Der höchste Koeffizient des charakteristischen Polynoms
![]() jeder Matrix
jeder Matrix
![]() ist 1, der konstante Koeffizient ist
ist 1, der konstante Koeffizient ist
![]() und der zweithöchste Koeffizient heißt
und der zweithöchste Koeffizient heißt
![]() .
Falls
.
Falls
![]() eine Matrizendarstellung von
eine Matrizendarstellung von
![]() ist, so ist
ist, so ist
![]() .
.
Beweis. Um den Koeffizienten von
14.3 Proposition.
Die Eigenwerte
![]() einer Isometrie erfüllen
einer Isometrie erfüllen
![]() .
.
Die Eigenwerte einer Spiegelung sind
![]() , die Eigenvektoren zu
, die Eigenvektoren zu
![]() bilden die Fixpunktmenge und der Eigenraum zu
bilden die Fixpunktmenge und der Eigenraum zu
![]() wird von
wird von
![]() erzeugt.
erzeugt.
Beweis.
Sei eine Spiegelung
![]() an
an
![]() gegeben.
Für
gegeben.
Für
![]() sind die Eigenwerte genau jene
sind die Eigenwerte genau jene
![]() mit
mit
![]() , d.h.
, d.h.
![]() .
Für
.
Für
![]() sind die Eigenwerte genau jene
sind die Eigenwerte genau jene
![]() mit
mit
![]() , d.h.
, d.h.
![]() also
o.B.d.A.
also
o.B.d.A.
![]() und
und
![]() , d.h.
, d.h.
![]() .
[]
.
[]
14.4 Beispiel.
Die Eigenwerte einer Drehung um den Winkel
![]() sind gegeben durch
sind gegeben durch
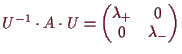 bezüglich der invertierbaren Matrix
bezüglich der invertierbaren Matrix
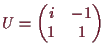 .
.
14.6 Lemma.
Alle Eigenwerte symmetrischer Matrizen
![]() sind reell.
sind reell.
Beweis. Es sei
14.7 Lemma.
Eigenvektoren zu verschiedenen Eigenwerten
![]() einer symmetrischen Matrix
einer symmetrischen Matrix
![]() stehen zueinander orthogonal.
stehen zueinander orthogonal.
Beweis. Es sei
14.8 Proposition.
Jede symmetrische
![]() besitzt eine orthonormal-Basis von Eigenvektoren
besitzt eine orthonormal-Basis von Eigenvektoren
![]() .
Es ist somit
.
Es ist somit
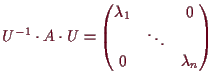
Beweis. Sei
14.8a Folgerung.
Es sei
![]() invertierbar, dann ist das Bild der Sphäre
invertierbar, dann ist das Bild der Sphäre
![]() ein Ellipsoid, genau gesagt gibt es eine
orthonormal-Basis von Eigenvektoren
ein Ellipsoid, genau gesagt gibt es eine
orthonormal-Basis von Eigenvektoren
![]() von
von
![]() mit zugehörigen
Eigenwerten
mit zugehörigen
Eigenwerten
![]() , s.d.
, s.d.
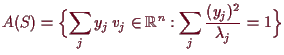
Beweis. Es ist
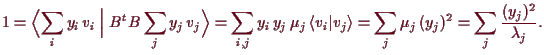
![\includegraphics[scale=1.2]{pic-1050}](img3623.png)
14.9 Bemerkung. Jordan'sche Normalform.
Allgemeine Matrizen
![]() lassen sich aber nicht immer
durch Konjugation
mit einer invertierbaren Matrix auf Diagonalgestalt bringen, wie obige Beispiele zeigen.
Dennoch läßt sich zeigen, daß folgendes erreicht werden kann:
Es sei
lassen sich aber nicht immer
durch Konjugation
mit einer invertierbaren Matrix auf Diagonalgestalt bringen, wie obige Beispiele zeigen.
Dennoch läßt sich zeigen, daß folgendes erreicht werden kann:
Es sei
![]() und
und
![]() die Eigenwerte in ihrer Vielfachheit
angeschrieben. Dann existiert ein linearer Isomorphismus
die Eigenwerte in ihrer Vielfachheit
angeschrieben. Dann existiert ein linearer Isomorphismus
![]() für welchen
für welchen
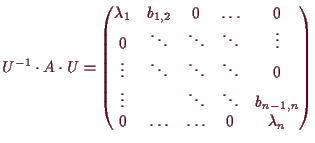
Ein erster Schritt um dies zu zeigen ist der
14.10 Satz von Cayley-Hamilton.
Es sei
![]() das charakteristische Polynom von
das charakteristische Polynom von
![]() . Dann ist
. Dann ist
![]() .
.
Beweis. Es sei
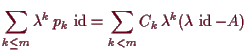
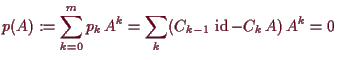
14.11 Bemerkung.
Falls
![]() regulär ist, so ist
regulär ist, so ist
![]() und somit
und somit
![]() aus
aus
![]() berechenbar.
berechenbar.
Andreas Kriegl 2002-02-01