Nächste Seite: 6 Die reellen Zahlen Aufwärts: Mathematik 1 für Informatik Vorherige Seite: 4 Die ganzen Zahlen Inhalt Index
5.1 Konstruktion von
![]() .
.
Wir wollen nun nach der additiven Gleichung
![]() die uns in (4.1)
zu den ganzen Zahlen geführt hat analog die multiplikative Gleichung
die uns in (4.1)
zu den ganzen Zahlen geführt hat analog die multiplikative Gleichung
![]() behandeln.
Nur für
behandeln.
Nur für
![]() dürfen wir die Existenz einer Lösung
dürfen wir die Existenz einer Lösung
![]() erhoffen, den
in jedem Ring gilt
erhoffen, den
in jedem Ring gilt
![]() für alle
für alle
![]() nach (2.6).
Leider haben wir für
nach (2.6).
Leider haben wir für
![]() gesehen, daß die Gleichung
gesehen, daß die Gleichung
![]() genau dann eine Lösung
genau dann eine Lösung
![]() besitzt, wenn
besitzt, wenn
![]() durch
durch
![]() teilbar ist.
Z.B. für
teilbar ist.
Z.B. für
![]() ist das nur für
ist das nur für
![]() der Fall.
der Fall.
Also versuchen wir wie in (4.1) wieder mit virtuellen Lösungen
![]() diesmal der Gleichungen
diesmal der Gleichungen
![]() für
für
![]() zu rechnen.
Analog zum Übergang von
zu rechnen.
Analog zum Übergang von
![]() auf
auf
![]() sollte
sollte
![]() sein und
sein und
![]() , falls
, falls
![]() ist.
Wir definieren also die Menge der rationalen Zahlen als
ist.
Wir definieren also die Menge der rationalen Zahlen als
Weiters sollte
![]() sein,
denn
sein,
denn
![]() .
Einfache Rechnungen zeigen, daß damit
.
Einfache Rechnungen zeigen, daß damit
![]() zu einem Körper wird,
der Körper der rationalen Zahlen.
Man schreibt natürlich üblicherweise
zu einem Körper wird,
der Körper der rationalen Zahlen.
Man schreibt natürlich üblicherweise
![]() an Stelle
von
an Stelle
von
![]() .
Beachte dabei, daß wir ganze Zahlen
.
Beachte dabei, daß wir ganze Zahlen
![]() als spezielle
rationale Zahlen
vermöge der Abbildung
als spezielle
rationale Zahlen
vermöge der Abbildung
![]() ,
,
![]() auffassen können.
auffassen können.
Kombinatorik (Fortsetzung)
5.2 Definition.
Unter einer Kombination ohne Wiederholung von
![]() vielen Objekten aus
vielen Objekten aus
![]() vielen,
versteht man eine Auswahl von
vielen,
versteht man eine Auswahl von
![]() -verschiedenen Elementen aus einer Grundmenge von
-verschiedenen Elementen aus einer Grundmenge von
![]() vielen, wobei
es auf die Reihenfolge der Auswahl nicht ankommen soll.
Also wenn z.B. der Vorstand bestehend aus 3 gleichberechtigen
Personen, deren jeweilige
Aufgaben/Ämter nicht
explizit festgelegt sind,
eines Vereins mit 100 Mitgliedern gewählt werden soll (ohne das Ämterkummulierung zulässig),
so ist eine Kombination ohne
Wiederholungen von 3 aus 100 zu bestimmen.
vielen, wobei
es auf die Reihenfolge der Auswahl nicht ankommen soll.
Also wenn z.B. der Vorstand bestehend aus 3 gleichberechtigen
Personen, deren jeweilige
Aufgaben/Ämter nicht
explizit festgelegt sind,
eines Vereins mit 100 Mitgliedern gewählt werden soll (ohne das Ämterkummulierung zulässig),
so ist eine Kombination ohne
Wiederholungen von 3 aus 100 zu bestimmen.
Kombinationen ohne Wiederholung von
![]() aus
aus
![]() werden also gerade
durch
werden also gerade
durch
![]() -Elementige Teilmenge einer
-Elementige Teilmenge einer
![]() -Elementigen Menge beschrieben.
-Elementigen Menge beschrieben.
5.3 Proposition.
Die Anzahl der Kombinationen ohne Wiederholung von
![]() vielen Objekten aus
vielen Objekten aus
![]() vielen
ist gerade der Binomialkoeffizient
vielen
ist gerade der Binomialkoeffizient
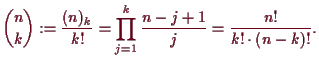
Beweis. Der Unterschied zwischen Variationen und Kombinationen ohne Wiederholung besteht gerade darin, daß es bei ersteren auf die Reihenfolge der Auswahlen ankommt. Aus jeder Auswahl einer Kombination ohne Wiederholung kann erhält man etliche Variationen ohne Wiederholung indem man die
Beachte, daß es genau eine Möglichkeit gibt aus
![]() -Elementen keines
Auszuwählen, nämlich die leere Menge, also ist
-Elementen keines
Auszuwählen, nämlich die leere Menge, also ist
![]() .
.
5.4 Folgerung. Binomsche Lehrsatz.
Für
![]() ist
ist
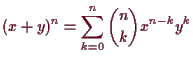
Beweis. Ausmultiplizieren von
5.5 Lemma.
Rekursionsformel für Binomialkoeffizienten:
![]()
Veranschaulichen kann man diese Rekursionsformel durch das Pascal'sches Dreieck, in welchen sich die Eintragungen als Summe des direkt darüber sowie des links darüberstehenden Elements ergeben:
![\bgroup\color{demo}$\displaystyle \begin{array}{ccccccc}
\binom{0}{0} \\ [0.2cm]...
...& \binom{n+1}{k+1}&\hdots&\hdots&\binom{n+1}{n+1} \\ [0.2cm]
\end{array}$\egroup](img1586.png)
Beweis. Dies läßt sich leicht mit Induktion zeigen, oder indem man beachtet, daß
5.6 Bemerkung.
Beachte, daß Kombinationen ohne Wiederholung von
![]() -Elementen aus
der Menge
-Elementen aus
der Menge
![]() , also
, also
![]() -elementige Teilmengen
-elementige Teilmengen
![]() , o.B.d.A. so geschrieben werden können,
daß
, o.B.d.A. so geschrieben werden können,
daß
![]() , also gerade durch streng monoton wachsende Folgen
von
, also gerade durch streng monoton wachsende Folgen
von
![]() natürlichen Zahlen
natürlichen Zahlen
![]() beschrieben werden können.
beschrieben werden können.
5.7 Definition.
Unter einer Kombination mit Wiederholung von
![]() vielen Objekten aus
vielen Objekten aus
![]() vielen,
versteht man eine Auswahl von
vielen,
versteht man eine Auswahl von
![]() Elementen aus einer Grundmenge von
Elementen aus einer Grundmenge von
![]() vielen,
wobei es auf die Reihenfolge der Auswahl nicht ankommen soll, und man durchaus auch
mehrmals gleiche Elemente wählen kann.
Man spricht auch von Auswählen mit Zurücklegen.
vielen,
wobei es auf die Reihenfolge der Auswahl nicht ankommen soll, und man durchaus auch
mehrmals gleiche Elemente wählen kann.
Man spricht auch von Auswählen mit Zurücklegen.
5.8 Bemerkung.
Jede Kombination mit Wiederholung von
![]() vielen Objekten aus
vielen Objekten aus
![]() vielen wird also
durch
vielen wird also
durch
![]() beschrieben, wobei wir verschiedene
Reihenfolgen der
beschrieben, wobei wir verschiedene
Reihenfolgen der
![]() als gleichbedeutend ansehen müssen.
Wir können aber wie bei Kombinationen ohne Wiederholung
die natürliche Reihenfolge
als gleichbedeutend ansehen müssen.
Wir können aber wie bei Kombinationen ohne Wiederholung
die natürliche Reihenfolge
![]() benutzen, und somit
Kombinationen mit Wiederholung als monoton wachsende Folgen von natürlichen
Zahlen
benutzen, und somit
Kombinationen mit Wiederholung als monoton wachsende Folgen von natürlichen
Zahlen
![]() auffassen.
auffassen.
5.9 Proposition.
Die Anzahl der Kombinationen mit Wiederholung von
![]() vielen Objekten aus
vielen Objekten aus
![]() vielen
ist
vielen
ist
![]() .
.
Beweis. Wir können aus jeder Kombination mit Wiederholung aufgefaßt als monotone Folge
Beispiel.
Es werden in einer Übungsstunde 10 Beispiele von gewissen der anwesenden
20 StudentInnen gerechnet. Wieviele Möglichkeiten bestehen dafür, wenn
es nur darauf ankommt dranzukommen, aber nicht welches Beispiel man rechnet.
Antwort: Kombinationen mit Wiederholung von 10 aus 20, also
![]() .
.
Zusammenfassung.
Wir haben also folgende Anzahlen für Auswahlen von
![]() aus
aus
![]() bestimmt:
bestimmt:
| mit Wiederholung | ohne Wiederholung | |
| mit Reihenf. (Variationen) |
|
|
| ohne Reihenf. (Kombinationen) |
|
|
Elementare Wahrscheinlichkeitstheorie
5.10 Definition.
Es sei eine Menge
![]() möglicher und gleich-wahrscheinlicher Ereignisse
gegeben. Also z.B.
möglicher und gleich-wahrscheinlicher Ereignisse
gegeben. Also z.B.
![]() Kopf
Kopf![]() Zahl
Zahl![]() bei Werfen einer Münze,
oder
bei Werfen einer Münze,
oder
![]() bei Werfen eines Würfels, oder
bei Werfen eines Würfels, oder
![]() beim Roulette.
Sei
beim Roulette.
Sei
![]() eine Teilmenge von
eine Teilmenge von
![]() .
Die Wahrscheinlichkeit
.
Die Wahrscheinlichkeit
![]() dafür, daß ein Ereignis aus
dafür, daß ein Ereignis aus
![]() eintritt
ist per Definition
eintritt
ist per Definition
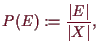
Offensichtlich ist
![]() . Es ist
. Es ist
![]() , wenn
, wenn
![]() ein sicher( eintretend)es Ereignis ist; und
ein sicher( eintretend)es Ereignis ist; und
![]() , wenn
, wenn
![]() ein unmögliches Ereignis ist.
ein unmögliches Ereignis ist.
So ist z.B. beim einmaligen Würfeln, ein einzelner Fall gerade ein
einzelner Wurf, der durch die oben liegende Ziffer des Würfels beschrieben
werden kann. Es gibt also 6 mögliche Fälle.
Sei nun das Ereignis
![]() gegeben, daß die Augenzahl gerade ist, dann sind
die Fälle
gegeben, daß die Augenzahl gerade ist, dann sind
die Fälle
![]() ,
,
![]() und
und
![]() günstig und somit
günstig und somit
![]() .
.
Beim Roulette hingegen ist die Anzahl der möglichen Fälle
![]() und die für ``rouge''(=rot) gerade
und die für ``rouge''(=rot) gerade
![]() , somit
, somit
![]() .
.
Beachte jedoch, daß es beim Werfen 2'er Münzen (oder auch beim
zweimaligen Werfen einer Münze) 4 mögliche Fälle gibt:
(Kopf,Kopf), (Kopf,Zahl), (Zahl,Kopf), (Zahl,Zahl).
Wenn wir also die Wahrscheinlichkeit des Ereignisses
![]() ,
daß genau eine Zahl kommt, bestimmen, so ergibt sich
,
daß genau eine Zahl kommt, bestimmen, so ergibt sich
![]() ,
und nicht ein Drittel wie an vielleicht fälschlich
wie folgt vermuten könnte: Es gibt 3 Fälle: Keinmal Kopf, genau einmal Kopf
und zweimal Kopf. Einer davon ist günstig, also
,
und nicht ein Drittel wie an vielleicht fälschlich
wie folgt vermuten könnte: Es gibt 3 Fälle: Keinmal Kopf, genau einmal Kopf
und zweimal Kopf. Einer davon ist günstig, also
![]() .
Diese Argumentation ist falsch, denn
genau einmal Kopf zu werfen, kann auf zwei Arten zustande kommen,
nämlich dadurch, daß die eine oder (ausschliesend)
die andere Münze auf Kopf fällt. Es ist also doppelt so wahrscheinlich
als, daß beide Münzen auf Kopf fallen.
.
Diese Argumentation ist falsch, denn
genau einmal Kopf zu werfen, kann auf zwei Arten zustande kommen,
nämlich dadurch, daß die eine oder (ausschliesend)
die andere Münze auf Kopf fällt. Es ist also doppelt so wahrscheinlich
als, daß beide Münzen auf Kopf fallen.
Beweis. Dies folgt aus
Beispiel.
Z.B. ist die Wahrscheinlichkeit bei 2 maligen Würfeln mindestens
einen 6'er zu haben wie folgt bestimmbar.
Die Wahrscheinlichkeit
![]() beim
beim
![]() -ten Wurf einen 6'er zu Würfeln
ist 1/6.
Die Wahrscheinlichkeit
-ten Wurf einen 6'er zu Würfeln
ist 1/6.
Die Wahrscheinlichkeit
![]() bei beiden Würfen einen
6'er zu Würfeln ist
bei beiden Würfen einen
6'er zu Würfeln ist
![]() , also ist
, also ist
![]() .
Dies hätten wir natürlich auch recht schnell durch Abzählen
der günstigen Fälle erhalten.
.
Dies hätten wir natürlich auch recht schnell durch Abzählen
der günstigen Fälle erhalten.
5.12 Satz über das Komplementärereignis.
![]() .
.
Beweis. Wegen
Beispiel.
Die Wahrscheinlichkeit dafür, daß mindestens zwei Personen auf einer Party
mit
![]() Personen am gleichen Tag Geburtstag haben berechnen wir wie folgt.
Das komplementäre Ereignis, daß keine 2 der Personen
am gleichen Tag Geburtstag haben ist
Personen am gleichen Tag Geburtstag haben berechnen wir wie folgt.
Das komplementäre Ereignis, daß keine 2 der Personen
am gleichen Tag Geburtstag haben ist
![]() . Bereits bei
. Bereits bei
![]() ist dies
ist dies
![]() also ist die Chance für 2 mit gleichen Geburtstag
bereits mehr als 50%.
also ist die Chance für 2 mit gleichen Geburtstag
bereits mehr als 50%.
5.13 Definition.
Unter der bedingten Wahrscheinlichkeit
![]() versteht man die Wahrscheinlichkeit dafür, daß
das Ereignis
versteht man die Wahrscheinlichkeit dafür, daß
das Ereignis
![]() eintritt, wenn man schon weiß, daß das Ereignis
eintritt, wenn man schon weiß, daß das Ereignis
![]() eintritt (oder eingetreten ist).
eintritt (oder eingetreten ist).
Z.B. sei beim zweimaligen Werfen einer Münze
![]() das Ereignis, daß die
erste Münze auf Kopf fällt und
das Ereignis, daß die
erste Münze auf Kopf fällt und
![]() das Ereignis, daß die zweite Münze
auf Kopf fällt. Dann hängt
das Ereignis, daß die zweite Münze
auf Kopf fällt. Dann hängt
![]() offensichtlich nicht von
offensichtlich nicht von
![]() ab, also
ist
ab, also
ist
![]() .
.
Hingegen ist beim zweifachen Ziehen einer Karte aus
![]() Karten (ohne die
erste zurückzustecken) die Wahrscheinlichkeit, daß die erste Karte ein
As ist
Karten (ohne die
erste zurückzustecken) die Wahrscheinlichkeit, daß die erste Karte ein
As ist
![]() . Jene, daß die zweite ein As ist hängt nun
aber davon ab ob wir bereits ein As gezogen und somit entfernt haben, dann ist
sie
. Jene, daß die zweite ein As ist hängt nun
aber davon ab ob wir bereits ein As gezogen und somit entfernt haben, dann ist
sie
![]() , oder ob wir beim ersten Zug kein As
erwischt haben, dann ist sie
, oder ob wir beim ersten Zug kein As
erwischt haben, dann ist sie
![]() .
.
5.14 Satz über die bedingte Wahrscheinlichkeit.
Es ist
![]() .
.
Beweis. Es ist
Diese Formel kann umgekehrt verwendet werden, um die Wahrscheinlichkeit
für das Eintreffen zweier Ereignisse
![]() und
und
![]() wie folgt zu bestimmen:
wie folgt zu bestimmen:
5.15 Multiplikationssatz.
Es ist
![]() .
Genau dann wenn
.
Genau dann wenn
![]() und
und
![]() unabhängig voneinander sind, d.h.
unabhängig voneinander sind, d.h.
![]() gilt, ist
gilt, ist
![]() .
.
Beweis. Die allgemeine Formel folgt sofort aus der Formel für die bedingte Wahrscheinlichkeit. Die spezielle Formel
Beispiel.
Die Wahrscheinlichkeit
![]() bei einem Kartenspiel
von 32 Karten ein As zu ziehen ist
bei einem Kartenspiel
von 32 Karten ein As zu ziehen ist
![]() .
Ist die gezogene Karte ein As, so ist die Wahrscheinlichkeit
.
Ist die gezogene Karte ein As, so ist die Wahrscheinlichkeit
![]() beim Ziehen einer weiteren Karten wieder ein As
zu ziehen
beim Ziehen einer weiteren Karten wieder ein As
zu ziehen
![]() . Die Wahrscheinlichkeit zwei Asse zu ziehen
ist somit
. Die Wahrscheinlichkeit zwei Asse zu ziehen
ist somit
![]() .
.
Vergleiche dies auch mit der Rechnung im Beispiel nach (5.12).
5.16 Formel für totale Wahrscheinlichkeit.
Beweis. Es ist
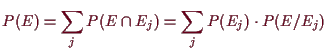
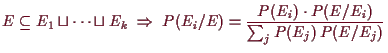
Beweis.
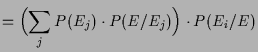 |
5.18 Beispiele.
Die Wahrscheinlichkeit bei Würfelpokern eine große Straße zu Würfeln
können wir wie folgt bestimmen. Es gibt
![]() möglichen Fälle für die 5 Würfe.
Ein günstiger wäre 10,B,D,K,A für 1.,2.,3.,4. und 5. Würfel, aber auch jede
andere der
möglichen Fälle für die 5 Würfe.
Ein günstiger wäre 10,B,D,K,A für 1.,2.,3.,4. und 5. Würfel, aber auch jede
andere der
![]() Anordnungen ist günstig, also ist
Anordnungen ist günstig, also ist
![]() .
.
Die Wahrscheinlichkeit bei Kartenpokern (wobei das Kartenspiel aus
9, 10, B, D, K, A in den 4 Farben bestehen soll) eine große Straße zu erhalten kann
wie folgt bestimmt werden:
Die Wahrscheinlichkeit
![]() als erste Karte ein As zu erhalten ist
als erste Karte ein As zu erhalten ist
![]() , jene
, jene
![]() für die zweite Karte einen König zu erhalten, wenn die
erste ein As war ist
für die zweite Karte einen König zu erhalten, wenn die
erste ein As war ist
![]() .
Die Wahrscheinlichkeit
.
Die Wahrscheinlichkeit
![]() ist somit
ist somit
![]() .
Jene, daß dann die 3.te Karte eine Dame ist, ist
.
Jene, daß dann die 3.te Karte eine Dame ist, ist
![]() , und somit
ist
die Wahrscheinlichkeit, daß die ersten 3 Karten
, und somit
ist
die Wahrscheinlichkeit, daß die ersten 3 Karten
![]() in dieser Reihenfolge
sind, gerade
in dieser Reihenfolge
sind, gerade
![]() .
Das wir
.
Das wir
![]() in dieser Reihenfolge erhalten hat analog
die Wahrscheinlichkeit
in dieser Reihenfolge erhalten hat analog
die Wahrscheinlichkeit
Die Wahrscheinlichkeit beim Würfelpoker ein full-hand mit sagen wir 2 Assen
und 3 Könige zu würfeln können wir analog wie folgt bestimmen:
Ein günstiger (der
![]() möglichen) Würfe wäre
möglichen) Würfe wäre
![]() .
Es gibt soviel Umordnungen dieses Falles wie 2-elementige Teilmengen
der Plätze 1 bis 5 die den Positionen der Asse entsprechen, also
ist die Wahrscheinlichkeit
.
Es gibt soviel Umordnungen dieses Falles wie 2-elementige Teilmengen
der Plätze 1 bis 5 die den Positionen der Asse entsprechen, also
ist die Wahrscheinlichkeit
![]() .
Es gibt
.
Es gibt
![]() verschiedene Arten von full-houses, also ist die
Wahrscheinlichkeit irgendein full-house zu würfeln
verschiedene Arten von full-houses, also ist die
Wahrscheinlichkeit irgendein full-house zu würfeln
![]() .
.
Beim Kartenspiel hingegen erhalten wir als Wahrscheinlichkeit von 2 Assen und 3 Königen
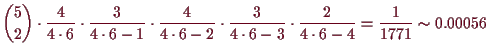
Andreas Kriegl 2002-02-01