Nächste Seite: 8 Vektorräume Aufwärts: Mathematik 1 für Informatik Vorherige Seite: 6 Die reellen Zahlen Inhalt Index
Von Leibniz stammt folgende Aussage aus 1702:
...imaginäre Wurzeln als feine und wunderbare Zuflucht des göttlichen Geistes, beinahe ein Zwitterwesen zwischen Sein und Nichtsein.Bzw. Euler 1768:
...dieselben ohnmögliche Zahlen sind. Der Begriff von solchen Zahlen, welche ihrer Natur nach ohnmöglich sind und gemeiniglich imaginäre Zahlen oder eingebildete Zahlen genannt werden, weil sie bloß allein in der Einbildung statt finden.
7.1 Bemerkung.
Keine Lösung von
![]() liegt in
liegt in
![]() .
.
Beweis. Angenommen eine Lösung, die wir mit
7.2 Definition. Körper der komplexen Zahlen.
Wir betrachten folglich eine virtuelle Lösung
![]() (die sogenannte imaginäre
Einheit) von
(die sogenannte imaginäre
Einheit) von
![]() und versuchen damit herumzurechnen. Insbesonders sollten wir reelle Zahlen
hinzuaddieren und hinzumultiplizieren können, also Ausdrücke der Form
und versuchen damit herumzurechnen. Insbesonders sollten wir reelle Zahlen
hinzuaddieren und hinzumultiplizieren können, also Ausdrücke der Form
![]() bilden können.
Da das kommutativ- und das distributiv-Gesetz auch hier gelten sollte
ergibt sich
bilden können.
Da das kommutativ- und das distributiv-Gesetz auch hier gelten sollte
ergibt sich
Die Addition von komplexen Zahlen als Punkten in der Ebene
entspricht somit der Addition der
(Orts)vektoren. Also ist die Addition mit einer fixen komplexen Zahl
![]() die Translation um den Vektor mit Koordinaten
die Translation um den Vektor mit Koordinaten
![]() .
.
![\includegraphics[scale=0.7]{pic-1035}](img1822.png)
Um auch die Multiplikation mit komplexen Zahlen geometrisch
zu beschreiben benötigen wir Polarkoordinaten, d.h. wir legen
Punkte nun durch den Abstand
![]() vom 0-Punkt und den Winkel
vom 0-Punkt und den Winkel
![]() von der
von der
![]() -Achse zum Ortsvektor fest.
Die kartesischen Koordinaten eines Punktes erhalten wird dann wie folgt
aus den Polarkoordinaten:
-Achse zum Ortsvektor fest.
Die kartesischen Koordinaten eines Punktes erhalten wird dann wie folgt
aus den Polarkoordinaten:
![\includegraphics[scale=0.7]{pic-1036}](img1836.png)
Die Multiplikation mit einer komplexen Zahl mit Polarkoordinaten
![]() ist nun gerade die Drehstreckung um den Winkel
ist nun gerade die Drehstreckung um den Winkel
![]() und den
Streckungsfaktor
und den
Streckungsfaktor
![]() , d.h.
Ein Punkt mit Polarkoordinaten
, d.h.
Ein Punkt mit Polarkoordinaten
![]() wird durch Multiplikation
mit
wird durch Multiplikation
mit
![]() auf den Punkt mit Polarkoordinaten
auf den Punkt mit Polarkoordinaten
![]() abgebildet.
abgebildet.
![\includegraphics[scale=0.7]{pic-1037}](img1840.png)
Rechnet man obige Beschreibung der Multiplikation komplexer Zahlen von Polarkoordinaten auf kartesische Koordinaten um so erhält man:
Der Körper
![]() kann aber leider nicht mehr angeordnet werden, denn
in jedem angeordneten Körper gilt
kann aber leider nicht mehr angeordnet werden, denn
in jedem angeordneten Körper gilt
![]() für alle
für alle
![]() und somit wäre
und somit wäre
![]() . Dann wäre aber
. Dann wäre aber
![]() nach (2.6)
ein Widerspruch.
nach (2.6)
ein Widerspruch.
7.7 Folgerung. Formel von Moivre.
Für
![]() und
und
![]() ist
ist
![]() .
.
Beweis. Dies folgt sofort durch Induktion aus der Darstellung der Multiplikation in Polarkoordinaten. []
7.8 Folgerung. Wurzeln komplexer Zahlen.
Es gibt genau
![]()
![]() -te Wurzeln jeder komplexen Zahl
-te Wurzeln jeder komplexen Zahl
![]() nämlich
nämlich
![]() für
für
![]() .
.
Beweis. Die Lösungen der Gleichung
Z.B. erhält man die 3-ten Einheitswurzeln, d.h. komplexen Zahlen
![]() mit
mit
![]() als
als
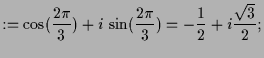 |
||
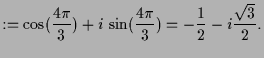 |
![\includegraphics[scale=0.7]{pic-1038}](img1871.png)
7.3 Lemma. Quadratische Gleichung.
Die (möglicherweise komplexen)
Lösungen der quadratischen Gleichung
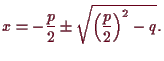
Beweis. Wir können die Gleichung wie folgt umformen:
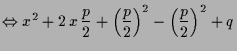 |
||
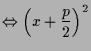 |
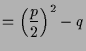 |
|
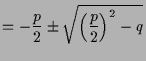 |
7.4 Bemerkung.
Es gibt die Cardano'schen Formeln für Lösungen
polynomiale Gleichungen 3. und 4. Ordnung.
Gleichungen höherer Ordnung lassen sich im Allgemeinen nicht mehr mittels Wurzelziehen auflösen. Jedoch gilt der
7.5 Fundamentalsatz der Algebra.
Jedes nicht-konstante Polynom
![]() besitzt eine Nullstelle in
besitzt eine Nullstelle in
![]() . Man sagt dafür auch,
. Man sagt dafür auch,
![]() ist algebraisch abgeschlossen.
ist algebraisch abgeschlossen.
Ein Beweis wäre an dieser Stelle nur sehr aufwendig zu führen.
7.6 Folgerung. Zerlegung in linear-Faktoren.
Jedes Polynom
![]() in
in
![]() läßt sich wie folgt
in linear-Faktoren zerlegen:
läßt sich wie folgt
in linear-Faktoren zerlegen:
Beweis. Wir machen Induktion nach
Beispiel.
Es sei
![]() . Dann ist offensichtlich
. Dann ist offensichtlich
![]() eine Nullstelle und
somit können wir (mittels Hornerschema)
eine Nullstelle und
somit können wir (mittels Hornerschema)
![]() durch
durch
![]() dividieren
und erhalten
dividieren
und erhalten
![]() .
Die Nullstellen von
.
Die Nullstellen von
![]() sind wegen (7.3) durch
sind wegen (7.3) durch
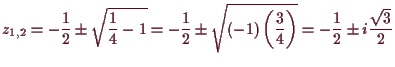
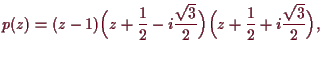
Bemerkung.
Komplexe Funktionen
![]() , wie z.B. Polynome
, wie z.B. Polynome
![]() ,
sind nach Definition Teilmengen von
,
sind nach Definition Teilmengen von
![]() und somit
schwer zu visualisieren.
Am besten ist wohl Definitionsbereich
und somit
schwer zu visualisieren.
Am besten ist wohl Definitionsbereich
![]() und Wertebereich
und Wertebereich
![]() getrennt
zu zeichnen, und die Funkion
getrennt
zu zeichnen, und die Funkion
![]() dadurch anzudeuten, daß man
gewisse Linien (wie z.B. konzentrische Kreise und Halbstrahlen durch 0)
im Definitionsbereich und deren Bilder unter
dadurch anzudeuten, daß man
gewisse Linien (wie z.B. konzentrische Kreise und Halbstrahlen durch 0)
im Definitionsbereich und deren Bilder unter
![]() im Wertebereich
einzeichnet.
Für die Funktion
im Wertebereich
einzeichnet.
Für die Funktion
![]() gibt dies z.B.
gibt dies z.B.
![\includegraphics[scale=1]{pic-1039}](img1907.png)
Es wird also die Ebene zweimal um den Nullpunkt herumgewickelt, und der Abstand der Punkte zum Nullpunkt dabei quadriert.
Diese Darstellung wird allerdings schnell kompliziert, denn z.B. für
![]() sieht sie so aus:
sieht sie so aus:
![\includegraphics[scale=1]{pic-1040}](img1909.png)
Eine andere Möglichkeit ist den Realteil
![]() und getrennt davon den Imaginärteil
und getrennt davon den Imaginärteil
![]() als Funktionen von
als Funktionen von
![]() und somit als Gebirge über der Ebene zu zeichnen.
Für
und somit als Gebirge über der Ebene zu zeichnen.
Für
![]() sieht das wie folgt aus:
sieht das wie folgt aus:
![\includegraphics[scale=1]{pic-1041}](img1914.png)
Resumeé
Wir haben nun alle wichtigen Zahlenbereiche durchbesprochen.
Es ist allerdings letztlich nicht so entscheidend was die Zahlen sind sondern
was sie können, d.h. daß wir
den vollständig angeordneten Körper
![]() und den algebraische abgeschlossenen
Körper
und den algebraische abgeschlossenen
Körper
![]() erhalten haben mit allen Konsequenzen die sich daraus ergeben.
Somit können wir frei nach Wittgenstein ``die Leiter wegwerfen, nachdem wir mit
ihrer Hilfe hinaufgestiegen sind''.
erhalten haben mit allen Konsequenzen die sich daraus ergeben.
Somit können wir frei nach Wittgenstein ``die Leiter wegwerfen, nachdem wir mit
ihrer Hilfe hinaufgestiegen sind''.
Wir sollten allerdings nicht alles von unterwegs vergessen,
denn einerseits haben wir ``mathematics at work'' gesehen. Z.B.
wie man durch Mengentheoretische Konstruktionen, Lösungen die von vornherein
nicht existieren so beschreiben und auf ein gesichertes Fundament stellen kann,
daß man wie gewünscht mit ihnen rechnen kann:
Beim Übergang von
![]() zu
zu
![]() waren die Elemente des kartesischen Produkts
waren die Elemente des kartesischen Produkts
![]() also Paare,
von
also Paare,
von
![]() zu
zu
![]() waren es Dedekind'sche Schnitte
(also Elemente der Potenzmenge
waren es Dedekind'sche Schnitte
(also Elemente der Potenzmenge
![]() ,
von
,
von
![]() zu
zu
![]() waren es Äquivalenzklassen von Paaren in
waren es Äquivalenzklassen von Paaren in
![]() und von
und von
![]() zu
zu
![]() Äquivalenzklassen von Paaren in
Äquivalenzklassen von Paaren in
![]() .
Gleichzeitig haben wir erkannt, daß Computer üblicherweise mit anderen Zahlen
(nämlich Restklassen modulo
.
Gleichzeitig haben wir erkannt, daß Computer üblicherweise mit anderen Zahlen
(nämlich Restklassen modulo
![]() ,
,
![]() oder ähnlichen) also in
oder ähnlichen) also in
![]() rechnen.
Wir haben dabei auch
kennengelernt, wie man mathematische Beweise führen kann, insbesonders die
Methode des indirekten Beweises und der vollständigen Induktion.
Weiters haben wir erste Einblicke in die Gebiete der Algebra (Gruppe, Ring,
Körper, etc.), der Kombinatorik (Permutation, Variation, Kombination, etc.),
der Zahlentheorie (Teilbarkeit, Primzahlen, ggT, etc.), der
Wahrscheinlichkeitstheorie, dem Rechnen mit Polynomen erhalten
sowie Verfahren (Algorithmen) wie man dies auch am Computer umsetzen kann.
rechnen.
Wir haben dabei auch
kennengelernt, wie man mathematische Beweise führen kann, insbesonders die
Methode des indirekten Beweises und der vollständigen Induktion.
Weiters haben wir erste Einblicke in die Gebiete der Algebra (Gruppe, Ring,
Körper, etc.), der Kombinatorik (Permutation, Variation, Kombination, etc.),
der Zahlentheorie (Teilbarkeit, Primzahlen, ggT, etc.), der
Wahrscheinlichkeitstheorie, dem Rechnen mit Polynomen erhalten
sowie Verfahren (Algorithmen) wie man dies auch am Computer umsetzen kann.
Andreas Kriegl 2002-02-01