Next: 5.1.8 Lathe Up: 5.1 Solid Finite Objects Previous: 5.1.6 Prism
We need curves passing through a finite number of given points.
In algebra we learn that there is exactly one polynomial ![]() of degree at most
of degree at most ![]() passing through
passing through ![]() points
points
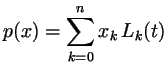 where
where 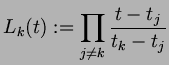
For a large number of points this becomes quite lengthy to calculate and for ![]() between the
given
between the
given ![]() the values can be quite far away from the
the values can be quite far away from the ![]() .
So the idea is to interpolate a fixed small number of successive points
and piece them together.
.
So the idea is to interpolate a fixed small number of successive points
and piece them together.
The simplest way would be to use linear interpolation of successive points and we would thus obtain a polygon.
But we could also take 3 (, 4 or more ) successive points and take the quadratic (, cubic, ...) polynomial connecting these and piece them together.
The disadvantage of this method will be that at the points, where we paste the pieces together the curve may take sharp turns, i.e. the left-sided and right-sided derivatives may be different.
To avoid this problem Bezier curves have been invented. In order to discuss them we need the Bernstein polynomials:
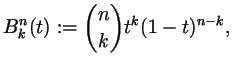
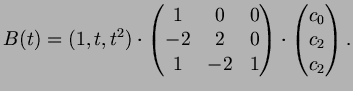
Now the Bezier curve of degree ![]() given by
given by ![]() many points
many points
![]() is given by
is given by
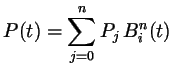
A geometric interpretation of this can be found in
graphics.cs.ucdavis.edu/.../Subdivision-Curves.pdf
The main properties of the Bezier curve ![]() are the following:
are the following:
Andreas Kriegl 2003-07-23