16.4 Stetige Gleichungen

Wir greifen nun das Problem auf (nicht-lineare) Gleichungen der Form $f(x)=y$ nach $x$ aufzulösen. Für quadratische und zum Teil auch für polynomiale Gleichungen haben wir dies bereits in der Mathematik I getan. Allgemein können wir O.B.d.A. $y=0$ voraussetzen, indem wir $f$ durch die Funktion $x\mapsto f(x)-y$ ersetzen. Die Existenz einer Lösung in gewissen Fällen liefert folgende

16.4.1 Proposition. Nullstellensatz von Bolzano.
Es sei $f:[a,b]\to\mathbb{R}$ stetig, mit $f(a)<0<f(b)$. Dann existiert ein $x\in[a,b]$ mit $f(x)=0$.

Beweis. Wir betrachten die Menge $A:=\{x\in[a,b]:f(x)\leq 0\}$. Diese ist beschränkt, besitzt also ein Supremum $\alpha :=\sup(A)$. Da $f$ stetig ist und $f\vert _A\leq 0$ gilt ist $f(\alpha )\leq 0$ und somit $\alpha <b$. Angenommen $f(\alpha )<0$. Wegen der Stetigkeit von $f$ bei $\alpha$ ist $f(x)$ ebenfalls kleiner als 0 für alle Punkte $x$ nahe $\alpha$, ein Widerspruch zu $\alpha =\sup(A)$.     []

16.4.2 Folgerung. Zwischenwertsatz.
Es sei $f:[a,b]\to\mathbb{R}$ stetig. Dann wird jeder Wert $y$ zwischen $f(a)$ und $f(b)$ angenommen werden.

Beweis. Falls $f(a)=f(b)$ so ist nichts zu zeigen. Sei also $y$ echt zwischen $f(a)$ und $f(b)$. Dann betrachten wir $g(x):=\frac{f(x)-y}{f(b)-f(a)}$. Es ist $g(b)>0$ und $g(a)<0$ also existiert nach dem Nullstellensatz (16.4.1) von Bolzano ein $x\in[a,b]$ mit $g(x)=0$, d.h. $f(x)=y$.     []

Regula falsi zur Nullstellenberechnung..
Wir können den Zwischenwertsatz (16.4.2) dazu verwenden, Nullstellen von Funktionen näherungsweise zu berechnen. Sei dazu $x_0$ und $x_1$ mit $f(x_0)\cdot f(x_1)<0$, d.h. $f(x_0)$ und $f(x_1)$ haben verschiedenes Vorzeichen. Wenn $f$ stetig ist, so existiert nach dem Nullstellensatz von Bolzano (16.4.1) eine Nullstelle $x_{\infty}$ zwischen $x_0$ und $x_1$. Um einen Näherungswert zu erhalten halbieren wir das Intervall und erhalten $x_2:=(x_0+x_1)/2$. Falls $f(x_2)=0$ so sind wir fertig. Andernfalls fahren wir wie zuvor mit $x_2$ und $x_0$ oder $x_1$ fort, je nachdem ob $f(x_2)\cdot f(x_0)<0$ oder $f(x_2)\cdot f(x_1)<0$. Die so erhaltene Folge $(x_0,x_1,\dots)$ konvergiert dann (da $\vert x_n-x_{n+1}\vert=\vert x_{n-1}-x_n\vert/2$) gegen eine Nullstelle $x_{\infty}$ von $f$.

Ein etwas ausgefeiltere Methode ist die Nullstelle der Sehne von $f$ als neuen Wert $x_2$ zu nehmen, d.h. die Lösung von $\frac{0-f(x_0)}{x_2-x_0}=\frac{f(x_1)-f(x_0)}{x_1-x_0}$, also

$$x_2:=x_0-f(x_0)\frac{x_1-x_0}{f(x_1)-f(x_0)}=\frac{x_0f(x_1)-x_1f(x_0)}{f(x_1)-f(x_0)}.$$

Und ansonsten wie zuvor vorzugehen. Die Konvergenz von $x_n$ ist nun aber nicht mehr so leicht einzusehen. Zwar sind die linken Grenzen $a_k$ und die rechten Grenzen $b_k$ monoton und somit konvergent gegen $\alpha$ bzw. $\beta$. Falls $\alpha =\beta$ so ist alles klar. Andernfalls ist $\alpha <\beta$. Falls $x_n$ fast immer die linke (oder die rechte) Grenze ist, so ist sie ebenfalls konvergent. Andernfalls seien $n_0<n_1<\dots$ die Stellen nach denen $x_n$ die Seite wechselt, d.h. $x_m=a_m$ für $m\in \{n_{2k-1}+1,\dots,n_{2k}\}$ und somit $b_m$ konstant für $m\in \{n_{2k-1},\dots,n_{2k}\}$, bzw. $x_m=b_m$ für $m\in\{n_{2k}+1,\dots,n_{2k+1}\}$ und somit $a_m$ konstant für $m\in\{n_{2k},\dots,n_{2k+1}\}$. Es sei $y_k:=x_{n_k}$. Für $m=n_{2k+1}$ ist

$$\alpha >a_{m+1}=x_{m+1} = a_m -f(a_m)\frac{b_m-a_m}{f(b_m)-f(a_m)} = a_m + \frac{b_m-a_m}{1-f(b_m)/f(a_m)}$$

also

$$\frac{\vert f(b_m)\vert}{\vert f(a_m)\vert}=\f... ...b_m-\alpha }{\alpha -a_m}>\frac{\beta -\alpha }{\alpha -a_m}\to+{\infty}$$ für $$m\to{\infty}.$$

Nach obigen ist $b_m=x_m=y_{2k+1}$ und $a_m=a_{n_{2k+1}}=\dots=a_{n_{2k}}=x_{n_{2k}}=y_{2k}$. Also ist $\vert f(y_{2k+1})\vert>2 \vert f(y_{2k})\vert$ für fast alle $k$. Analog zeigt man

$$\frac{\vert f(y_{2k})\vert}{\vert f(y_{2k-1})\vert} \geq \frac{\beta -\alpha }{b_{n_{2k-1}}-\beta }\to+{\infty},$$

also ebenfalls $\vert f(y_{2k})\vert\geq 2\vert f(y_{2k-1})\vert$ für fast alle $k$. Dies zeigt die Unbeschränktheit von $f$.

Eine andere Möglichkeit Gleichungen der Form $f(x)=y$ zu lösen, ist inverse Funktionen $f^{-1}$ zu finden und damit die Lösung als $x=f^{-1}(y)$ erhalten. Wir wollen nun dieses Problem der Invertierbarkeit (nicht-linearer) Funktionen $f:\mathbb{R}^p\supseteq X\to \mathbb{R}^q$ in Angriff nehmen. Dazu beginnen wir vorerst im Fall $f:\mathbb{R}\supseteq I\to \mathbb{R}$, wobei $I$ ein Intervall ist. Falls $f$ injektiv ist, so muß $f$ streng monoton sein, denn andernfalls existieren $x_0<x_1<x_2$ in $I$, sodaß $f(x_0)$ und $f(x_2)$ auf der selben Seite von $f(x_1)$ liegen. O.B.d.A. liege $f(x_0)$ näher an $f(x_1)$ als $f(x_2)$. Dann existiert nach dem Zwischenwertsatz ein $y_0$ zwischen $x_1$ und $x_2$ mit $f(x_0)=f(y_0)$, ein Widerspruch zur Injektivität von $f$.

Wir können uns in unseren Überlegungen also auf streng monotone Funktionen beschränken. Beachte jedoch, daß dies nur für Intervalle gilt, denn $x\mapsto 1/x$ ist bijektiv $\mathbb{R}\setminus\{0\}\to\mathbb{R}\setminus\{0\}$ aber nicht streng monoton.

16.4.4 Theorem über die Inverse monotoner Funktionen.
Es sei $f:I\to\mathbb{R}$ streng monoton wachsend auf einem Intervall $I$. Dann ist $f:I\to f(I)$ bijektiv mit streng monotoner und stetiger Inversen $f^{-1}$. Ist $f$ zusätzlich stetig, so ist $f(I)$ ebenfalls ein Intervall.

Klarerweise heißt $f$ streng monoton wachsend, wenn $f(x)<f(y)$ aus $x<y$ folgt.

Beweis. Offensichtlich ist $f$ bijektiv und die Inverse $f^{-1}$ streng monoton wachsend.

Nun zur Stetigkeit: Sei $f(\xi )=\eta$. Wir betrachten zuerst den Fall wo $\xi$ ein innerer Punkt von $I$ ist. Für (kleine) $\varepsilon >0$ ist $\xi \pm\varepsilon \in I$ und somit $f(\xi -\varepsilon )<f(\xi )=\eta <f(\xi +\varepsilon )$. Nun wählen wir ein $\delta >0$ mit $f(\xi -\varepsilon )<\eta -\delta <\eta +\delta <f(\xi +\varepsilon )$ und somit ist für $\vert y-\eta \vert<\delta$ auch $\xi -\varepsilon =f^{-1}(f(\xi -\varepsilon ))<f^{-1}(y)<f^{-1}(f(\xi +\varepsilon ))=\xi +\varepsilon$, d.h. $\vert f^{-1}(y)-f^{-1}(\eta )\vert<\varepsilon$.

Falls $\xi$ ein Randpunkt von $I$ ist (z.B. der linke), so gehen wir genauso vor, benötigen allerdings nur die Hälfte der Ungleichungen: Es ist $\xi +\varepsilon \in I$ für kleine $\varepsilon >0$ und somit $f(\xi )=\eta <f(\xi +\varepsilon )$. Nun wählen wir ein $\delta >0$ mit $f(\xi )<\eta +\delta <f(\xi +\varepsilon )$ und somit ist für $\vert y-\eta \vert<\delta$ auch $\xi =f^{-1}(f(\xi ))<f^{-1}(y)<f^{-1}(f(\xi +\varepsilon ))=\xi +\varepsilon$, d.h. $\vert f^{-1}(y)-f^{-1}(\eta )\vert<\varepsilon$.

Sei nun $f$ stetig. Dann ist $f(I)$ ein Intervall, denn nach dem Zischenwertsatz wird jeder Wert $\inf(f(I))<y<\sup(f(I))$ angenommen.     []

16.4.5 Beispiele. Wurzel und trigonometrische Funktionen.
Nach dem inversen Funktionensatz (16.4.4) ist für $n\geq 1$ die Umkehrfunktion zu $x\mapsto x^n$, $\{t\in\mathbb{R}:t\geq 0\}\to \{t\in\mathbb{R}:t\geq 0\}=:\mathbb{R}^+$ wohldefiniert, stetig und streng monoton wachsend. Da $0^n=0$ und $\lim_{x\to{\infty}}x^n=+{\infty}$, ist die $n$-te Wurzel als Umkehrfunktion $y\mapsto \root{n}\of{y}$ auf ganz $\mathbb{R}^+$ definiert.

Entsprechend folgt auch die Existenz einer stetigen, monoton wachsenden Umkehrfunktion $\arcsin:[-1,1]\to [-\pi/2,\pi/2]$, $\arccos:[-1,1]\to [-\pi,0]$ und $\arctan:\mathbb{R}\to (-\pi/2,\pi/2)$.

16.4.6 Banach'scher Fixpunktsatz.
Anstelle einer Gleichung der Form $f(x)=y$ können wir äquivalent auch die Fixpunkt-Gleichung $x=g(x):=x+y-f(x)$ lösen. Wenn $x_0$ nicht ein Fixpunkt von $g$ ist, dann betrachten wir $x_n$ rekursiv definiert durch $x_{n+1}:= g(x_n)$. Wir hätten gerne, daß $x_{\infty}:=\lim_n x_n$ existiert, da dann $g(x_{\infty})=g(\lim_n x_n)=\lim_n g(x_n)= \lim_n x_{n+1}=x_{\infty}$, d.h. $x_{\infty}$ ein Fixpunkt wäre. Dazu brauchen wir, daß $d(x_{n+1},x_{\infty})=d(g(x_n),g(x_{\infty}))\to 0$, oder besser $d(g(x),g(y))< d(x,y)$, oder sogar $d(g(x),g(y))\leq q d(x,y)$ mit $q<1$. Dann ist

$$d(x_{n+1},x_n) = d(g^n(x_1),g^n(x_0)) \leq q^n d(x_1,x_0)$$

$$d(x_{n+m},x_n) \leq \sum_{k=0}^{m-1} d(x_{n+k+1},x_{n+k}) \leq\sum_{k=0}^{m-1}q^k d(x_{n+1},x_n)$$

$$\leq \sum_{k=0}^{m-1} q^{n+k} d(x_1,x_0) \leq \frac{q^n}{1-q} d(x_1,x_0)\to 0,$$

daher ist $x_n$ eine Cauchy-Folge und konvergiert also zu einem Fixpunkt $x_{\infty}$. Wenn $x$ ein weiterer Fixpunkt ist, dann ergibt $d(x,x_{\infty})=d(g(x),g(x_{\infty}))< d(x,x_{\infty})$ einen Widerspruch. Beachte, daß

$$\begin{multline*} d(x_{n+m},x_n) \leq \sum_{k=0}^{m-1} d(x_{n+k+1},x_{n+k}) \leq... ...leq \frac{q}{1-q} d(x_n,x_{n-1}) \leq \frac{q^n}{1-q} d(x_1,x_0) \end{multline*}$$

und daher

$$d(x_{\infty},x_n) \leq \frac{q}{1-q} d(x_n,x_{n-1}) \leq \frac{q^n}{1-q}d(x_1,x_0).$$

Dies zeigt:

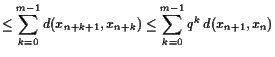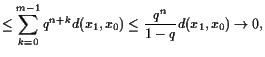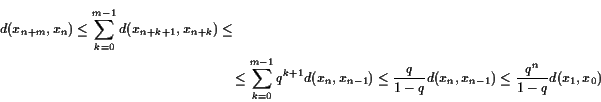
Banach'scher Fixpunkt-Satz.
Es sei $(X,d)$ ein vollständiger metrischer Raum und $g:X\to X$ eine Kontraktion, d.h. ein $q<1$ existiert mit $d(g(x),g(y))\leq q d(x,y)$ für alle $x,y\in X$. Dann gibt es einen eindeutigen Fixpunkt $x_{\infty}\in X$ von $g$, welcher als Limes der rekursiv definierten Folge $x_{n+1}:= g(x_n)$ mit beliebigen Startwert $x_0$ erhalten werden kann. Weiters gelten die Abschätzungen

$$d(x_{\infty},x_n) \leq \frac{q}{1-q} d(x_n,x_{n-1}) \leq \frac{q^n}{1-q}d(x_1,x_0).{\rm\quad[]}$$