17.1 Differenzierbarkeit

Wir wollen nun die Ableitung von Abbildungen $f:E\to F$ zwischen endlich dimensionalen reellen Vektorräumen $E$ und $F$ behandeln. Sei dazu vorerst $E=F=\mathbb{R}$. In den motivierenden Beispielen in (15.1.1) und (15.1.4) war uns bereits die geometrische Idee der Ableitung als Tangente an $f$ in einem Punkt begegnet. Um diese Gerade zu beschreiben benötigen wir neben dem Berührpunkt auch ihren Anstieg. Dieser sollte offensichtlich der Grenzwert der Anstiege von Sehnen benachbarter Punkte sein. Also

17.1.1 Definition. Ableitung von Kurven.
Es sei $f:\mathbb{R}\supseteq I\to \mathbb{R}$ eine Abbildung auf einem Intervall $I$. Die Ableitung von $f$ bei $x_0$ ist dann definiert als

$$f'(x_0) := \lim_{I\ni x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=\lim_{v\to 0}\frac{f(x_0+v)-f(x_0)}{v}.$$

Man schreibt auch $\frac{df(x)}{dx}$ oder uneindeutiger $\frac{df}{dx}$ für diesen Grenzwert und sagt Differentialquotient dafür. Falls dieser Grenzwert existiert, so heißt $f$ differenzierbar an der Stelle $x_0$. Falls $f$ in allen Punkten $x_0\in I$ differenzierbar ist, so heißt $f$ differenzierbar und die Abbildung $f':I\to\mathbb{R}$, $x_0\mapsto f'(x_0)$ heißt dann Ableitung von $f$.

Die Tangente an eine im Punkte $x_0$ differenzierbare Abbildung $f$ ist nun der affine 1-dimensionale Teilraum $\{(x,y)\in\mathbb{R}^2:y-f(x_0)=f'(x_0)(x-x_0)\}\subseteq \mathbb{R}^2$.

Für $f:\mathbb{R}\supseteq I \to\mathbb{R}^q$ macht obige Definition von $f'(x_0)$ ebenfalls Sinn. Allerdings ist $f(x)-f(x_0)\in\mathbb{R}^q$, $x-x_0\in\mathbb{R}$ und somit $\frac{f(x)-f(x_0)}{x-x_0}$ und $f'(x_0)$ in $\mathbb{R}^q$. Die Tangente ist dann entsprechend der affine 1-dimensionale Teilraum $\{(x,y):y-f(x_0)=f'(x_0)(x-x_0)\}$ von $\mathbb{R}\times \mathbb{R}^q$.

17.1.2 Beispiele differenzierbarer Funktionen.

1. Es sei $f:\mathbb{R}\to\mathbb{R}^q$ konstant.
   Dann ist $f$ differenzierbar und $f'(x_0)=\lim_{v\to 0}\frac{0}{v}=0$.
2. Sei nun $f:=\operatorname{id}:\mathbb{R}\to\mathbb{R}$.
   Dann ist $f$ differenzierbar und $f'(x_0)=\lim_{v\to 0}\frac{v}{v}=1$.
3. Sei schließlich $f:\mathbb{R}\to\mathbb{R}^q$ eine Gerade gegeben durch $f(x):=x a+b$ mit $a,b\in\mathbb{R}^q$.
   Dann ist $f$ differenzierbar und $f'(x_0)=\lim_{v\to 0}\frac{a v+b-b}{v}=a$ und somit stimmt die Tangente mit der Gerade überein.
4. Sei $f(x):=\vert x\vert$, dann ist $f$ nicht differenzierbar bei 0, denn
   $$\lim_{v\to0+}\frac{f(x+v)-f(x)}{v}=+1$$ aber $$\lim_{v\to0-}\frac{f(x+v)-f(x)}{v}=-1.$$

5. Es sei $f(x):=\frac1x$. Dann ist $f'(x)=-\frac1{x^2}$ für $x\ne 0$ wie eine direkte Berechnung des Differentialquotienten $\frac{df(x)}{dx}$ zeigt.
6. Sei $f(x):=\sin(x)$. Dann ist $f$ differenzierbar bei 0 mit Ableitung $1$, denn durch Flächenvergleich (siehe nmb!16.1.8) erhalten wir $\sin(t)\leq t\leq \tan(t)$ für $t>0$ und somit $\cos(t)\leq \frac{\sin(t)}{t}\leq 1$ und $\lim_{t\to 0}\cos(t)=1$. Weiters ist $f$ differenzierbar bei jedem $x\in\mathbb{R}$ mit Ableitung $\sin'(x)=\cos(x)$, denn
   $$\frac{\sin(x+v)-\sin(x)}{v}= \frac{\cos(x+v/2)\sin(v/2)}{v/2}\to \cos(x) 1.$$

Bemerkung.
Gewisse Eigenschaften der Funktion $f:\mathbb{R}\supseteq I\to \mathbb{R}$ lassen sich in Eigenschaften der Ableitung $f'$ übersetzen. Ist z.B.  $f$ monoton wachsend, d.h.  $f(x)\leq f(y)$ für $x\leq y$, so ist der Differenzenquotient $\frac{f(y)-f(x)}{y-x}\geq 0$ für alle $x\ne y$ und somit auch $f'(x)=\lim_{y\to x} \frac{f(y)-f(x)}{y-x}\geq 0$. Um die Umkehrung zu zeigen benötigen wir folgende Resultate:

17.1.3 Satz von Rolle.
Es sei $f:[a,b]\to\mathbb{R}$ stetig sowie auf $(a,b)$ differenzierbar und $f(a)=f(b)$. Dann existiert ein $\xi \in(a,b)$ mit $f'(\xi )=0$.

Beweis. Falls $f$ konstant ist, so ist nichts zu zeigen. Andernfalls nimmt $f$ sein Minimum an einer Stelle $\xi _1\in[a,b]$ an und sein Maximum an einer Stelle $\xi _2\in[a,b]$. Wegen $\xi _1\ne\xi _2$ liegt mindestens eines der beiden $\xi$ im Inneren $(a,b)$ des Intervalls $[a,b]$ und für dieses gilt $f'(\xi )=0$, denn aus $f(x)\geq f(\xi )$ für alle $x$ folgt $f'(\xi )=\lim_{t\to 0+}\frac{f(x)-x(\xi )}{x-\xi }\geq 0$ und ebenso $f'(\xi )=\lim_{t\to 0-}\frac{f(x)-x(\xi )}{x-\xi }\leq 0$, und ähnlich für $f(x)\leq f(\xi )$.     []

17.1.4 Mittelwertsatz.
Es sei $f,g:[a,b]\to\mathbb{R}$ stetig und auf $(a,b)$ differenzierbar. Dann existiert ein $\xi \in(a,b)$ mit

$$(f(b)-f(a)) g'(\xi ) = (g(b)-g(a)) f'(\xi ),$$

oder einprägsamer

$$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi )}{g'(\xi )},$$

falls $g'(x)\ne 0$ für alle $x\in (a,b)$.

Ist speziell $g=\operatorname{id}$ so besagt diese Gleichung folgendes:

$$\frac{f(b)-f(a)}{b-a}=f'(\xi ).$$

Beweis. Wir erhalten das Resultat direkt, wenn wir den Satz von Rolle auf $h(x):=(f(b)-f(a)) g(x)-(g(b)-g(a)) f(x)$ anwenden.     []

17.1.5 Folgerung. Monotonie via Ableitung.
Es sei $f:[a,b]\to\mathbb{R}$ stetig und auf $(a,b)$ differenzierbar. Dann ist $f$ genau dann monoton wachsend, wenn $f'(x)\geq 0$ für alle $x\in (a,b)$. Ebenso ist $f$ genau dann monoton fallend, wenn $f'(x)\leq 0$ für alle $x\in (a,b)$.

Beweis. Aus $f(x)\leq f(y)$ für alle $x\leq y$ folgt $f'(x)=\lim_{y\to x} \frac{f(y)-f(x)}{y-x}\geq 0$.

Umgekehrt folgt aus dem $\frac{f(x)-f(y)}{x-y}=f'(\xi )\geq 0$, daß $f$ monoton wachsend ist.     []

17.1.6 Regel von De L'Hospital.
Die Funktionen $f$ und $g$ seien differenzierbar auf $(a,b)$ mit $g'(x)\ne 0$ für alle $x$. Weiters sei $\lim_{x\to a+}f(x)=\lim_{x\to a+}g(x)=0$. Dann ist

$$\lim_{x\to a+}\frac{f(x)}{g(x)} = \lim_{x\to a+}\frac{f'(x)}{g'(x)},$$

sofern der Limes auf der rechten Seite im eigentlichen oder uneigentlichen Sinn existiert.

Beweis. Es sei $\lambda :=\lim_{x\to a+}\frac{f'(x)}{g'(x)}$, d.h. für jedes $\varepsilon >0$ existiert ein $\delta >0$ s.d. $\vert f'(x)/g'(x)-\lambda \vert<\varepsilon$ für alle $a<x<a+\delta$. Für $a<x<y<a+\delta$ ist nach dem Mittelwertsatz

$$\frac{f(y)-f(x)}{g(y)-g(x)}=\frac{f'(\xi )}{g'(\xi )}$$

für ein $\xi \in[x,y]$, also auch

$$\left\vert\frac{f(y)-f(x)}{g(y)-g(x)}-\lambda \right\vert<\varepsilon .$$

Der Grenzübergang $x\to a+$ liefert somit

$$\left\vert\frac{f(y)}{g(y)}-\lambda \right\vert\leq\varepsilon ,$$

also ist auch $\lim_{x\to a+}\frac{f(x)}{g(x)}=\lambda$.     []

17.1.10 Beispiel.
Nach der Regel (17.1.6) von De L'Hospital ist

$$\lim_{t\to 0}\frac{\sin(t)}{t} = \lim_{t\to 0}\frac{\cos(t)}{1}=\cos(0)=1,$$

vgl. dies mit (17.1.26).

17.1.7 Definition. Ableitung von Abbildungen.
Wir wollen nun auch die Ableitung für Abbildungen $f:E\to F$ zwischen allgemeinen endlich dimensionalen Vektorräumen $E$ und $F$ definieren. Dabei können wir nicht mehr $\frac{f(x_0+v)-f(x_0)}{v}$ bilden, da wir Vektoren nicht dividieren können. Die geometrische Idee in (17.1.1), daß die Ableitung gerade jene lineare Funktion $a:v\mapsto f'(x_0) v$ beschreibt, welche die nach 0 verschobene Funktion $f$ gut approximiert, ist aber auf den allgemeinen Fall übertragbar. Wenn $(x_0,f(x_0))\in E\times F$ beliebig ist, dann verschieben wir diesen Punkt nach $(0,0)$, d.h. wir ersetzen $x$ durch $x-x_0=:v$ und $y$ durch $y-f(x_0)$ und somit $f:x\mapsto f(x)$ durch die nach $(0,0)$ verschobene Funktion $\tilde f:v\mapsto x:=x_0+v \mapsto f(x)=f(x_0+v)\mapsto f(x_0+v)-f(x_0)$:

$$\xymatrix{ v+x_0 &x\ar[1,0] &E\ar[-0,1]^{f} &F... ...1,0] &x-x_0 &E\ar[-1,0]^{\cong} \ar[-0,1]^{\tilde f} &F & y-f(x_0) \\ }$$

Für differenzierbare Funktionen $f:\mathbb{R}\to F$ gilt

$$\frac{(\tilde f-a)(v)}{v}=\frac{f(x_0+v)-f(x_0)-f'(x_0) v}{v} =\frac{f(x_0+v)-f(x_0)}{v}-f'(x_0)\to 0.$$

Dies führt zur folgenden Definition: Es seien $E$ und $F$ endlich dimensionale Vektorräume und $U\subseteq E$ offen (d.h. zu jedem Punkt $x_0\in U$ existiert ein Ball $U_r(x_0)\subseteq U$ mit Radius $r>0$). Weiter sei $f:E\supseteq U\to F$ und $x_0\in E$. Dann heißt $f$ differenzierbar bei $x_0$ falls eine lineare Abbildung $a:E\to F$ existiert, welche die nach 0 verschobene Abbildung $\tilde f:v\mapsto f(x_0+v)-f(x_0)$ im folgenden Sinn approximiert:

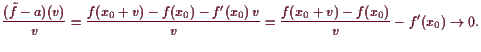
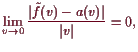$$\lim_{v\to 0}\frac{\vert\tilde f(v)-a(v)\vert}{\vert v\vert}=0,$$ oder äquivalent auch $$\lim_{v\to 0}\frac1{\vert v\vert}\Bigl(\tilde f(v)-a(v)\Bigr)=0.$$

Die lineare Abbildung $a$ ist sofern sie existiert eindeutig festgelegt (wie wir gleich zeigen werden) und heißt Ableitung $f'(x_0)$. Eine Abbildung $f:E\supseteq U\to F$ heißt differenzierbar, falls $f$ in allen Punkten $x_0$ differenzierbar ist. Ihre Ableitung ist die Abbildung

$$f':E\to L(E,F),\quad x_0\mapsto f'(x_0).$$

17.1.8 Definition. Richtungsableitung.
Wir wollen nun eine Methode finden die lineare Approximation im Sinn von (17.1.7) zu bestimmen, und damit auch gleichzeitig ihre Eindeutigkeit beweisen. Dazu betrachten wir den die Differenzierbarkeit definierenden Grenzwert, variieren dabei aber die Variable $v$ nur längs einer Geraden durch 0, d.h. wir betrachten nur $v$ der Gestalt $tv$ mit $t\in\mathbb{R}$ und fixen $v$. Falls $f$ bei $x$ differenzierbar ist und $a\in L(E,F)$ eine, wie für die Differenzierbarkeit geforderte, lineare Abbildung ist, so ist auch dieser eingeschränkte Grenzwert 0, d.h.

$$0= \lim_{t\to 0} \frac{f(x+tv) -f(x)-a(tv)}{\V... ...ame{sgn}(t)}{\Vert v\Vert} \Bigl(\frac{f(x+tv) -f(x)}{t} - a(v)\Bigr).$$

Multiplizieren wir dies mit der beschränkten Abbildung $t\mapsto \operatorname{sgn}(t)\Vert v\Vert$ so erhalten wir

$$a(v) = \lim_{t\to 0} \frac{f(x+tv)-f(x)}{t} = (f_{x,v})'(0),$$

wobei $f_{x,v}:\mathbb{R}\to F$ die Abbildung $f$ längs der Geraden $t\mapsto x+tv$ ist, d.h. $f_{x,v}(t):= f(x+tv)$.

Unter der Richtungsableitung $d_vf(x)$ von $f$ bei $x$ in Richtung $v\in E$ verstehen wir folglich

$$d_vf(x) := \lim_{t\to 0+} \frac{f(x+t v)-f(x)}{t}\in F.$$

Falls also $f$ bei $x$ differenzierbar ist, so existiert $d_vf(x)$ für alle $v\in E$ und es ist $d_vf(x)=a(v)$.

Somit ist das $a\in L(E,F)$ in der Definition der Differenzierbarkeit von $f$ bei $x$ eindeutig bestimmt und wird zu recht als Ableitung $f'(x):=a$ von $f$ bei $x$ bezeichnet.

Es ist $d_{s v} f(x)=s d_v f(x)$ für $s\geq 0$ (d.h. positiv homogen), denn für $s=0$ sind beide Seiten 0, und für $s>0$ haben wir

$$d_{s v} f(x) = \lim_{t\to 0+}\frac{f(x+tsv)-f(x)}t = s\; \lim_{ts\to 0+} \frac{f(x+tsv)-f(x)}{ts} = s\; d_v f(x).$$

Ist insbesonders $E=\mathbb{R}$, dann können wir die linearen Abbildungen $a:E\to F$ mit ihren Werten $a(1)\in F$ vermöge $a(v)=a(v\cdot 1)=v\cdot a(1)$ identifizieren.

$$L(\mathbb{R},F)\to F ,\quad a\mapsto a(1)$$

$$L(\mathbb{R},F)\gets F ,\quad (t\mapsto tv) \DOTSB\kern.2em\setbox0=\hbox{$\leftarrow$\kern-.15em\raise0.1ex\hbox{$\vert$}}\box0 \kern.3emv.$$

In diesem Sinn ist die Ableitung $f'(x)\in L(E<F)$ einer Abbildung $f:\mathbb{R}\supseteq U\to F$ bei $x$ als Element in $F$ auffaßbar. Dieses ist durch den Differentialquotienten

$$d_1 f(x) = \lim_{t\to 0+} \frac{f(x+t)-f(x)}{t}$$

gegeben. Dies zeigt, daß die Definition (17.1.7) im Falle $E=\mathbb{R}$ mit jener aus (17.1.1) für Kurven gleichbedeutend ist.

Man schreibt oft auch allgemein $a\cdot h$ für $a(h)$.

Falls $E=\mathbb{R}^p$, dann haben wir ausgezeichnete Richtungen, nämlich jene die durch die Standard-Basis $e_1,\dots,e_p\in \mathbb{R}^p$ gegeben sind. Folglich haben wir auch die ausgezeichneten Richtungsableitungen

$$\d _i f(x) := d_{e_i} f(x) = \left.\frac{d}{dt}\right\vert _{t=0} f(x+t e_i),$$

die auch als partielle Ableitungen

$$\frac{\d f}{\d x_i} (x_1,\dots,x_p) = \frac{\d }{\d x_i} f(x_1,\dots,x_p)$$

bezeichnet werden. Es ist

$$\frac{\d f}{\d x_i} (x_1,\dots,x_p) := \frac{d}{dt}\vert _{t=0} f(x_1,\dots,x_{i-1},x_i+t,x_{i+1},\dots,x_p),$$

also die Ableitung von $f$ an der Stelle $x_i$, wenn man alle anderen Koordinaten $x_1,\dots,x_{i-1},x_{i+1},\dots,x_p$ festhält.

17.1.9 Proposition. Differenzierbarkeit via Richtungableitungen.
Eine Abbildung $f:E\supseteq U\to F$ ist genau dann differenzierbar bei $x$, wenn folgende Punkte erfüllt sind:

(1)

$d_vf(x)$ existiert für alle $v\in E$;

(2)

$v\mapsto d_vf(x)$ ist linear;

(3)

$\frac{f(x+tv)-f(x)}t\to d_vf(x)$ für $t\to 0+$ glm. bzgl. $\Vert v\Vert=1$.

Beweis. Nach obigen Bemerkungen existieren für eine differenzierbare Abbildung $f$ alle Richtungsableitungen und es ist $f'(x)=a:v\mapsto d_vf(x)$ linear und stetig. Umgekehrt setzen wir $a(v):=d_vf(x)$. Wenn wir die Polarzerlegung $h=t v$ mit $t:=\Vert h\Vert\geq 0$ und $v:=\frac1{\Vert h\Vert}h$ verwenden so übersetzt sich der die Ableitbarkeit definierende Limes wie folgt:

$$= \lim_{h\to 0}\frac{f(x+h)-f(x)-a(h)}{\Vert h\Vert}$$ 0

$$= \lim_{t\to 0+,\Vert v\Vert=1} \frac1{\Vert v\Vert}\;\Bigl(\frac{f(x+t v)-f(x)}{t}-a(v)\Bigr)$$

$$\Leftrightarrow\quad a(v) = \lim_{t\to 0+} \frac{f(x+t v)-f(x)}{t} \Vert v\Vert=1{\rm\quad[]}$$

Wir schreiben von nun an auch $f'(x)(v)$ anstelle $d_vf(x)$, selbst in dem Fall, wo nur die Richtungsableitungen nicht aber die Ableitung existiert.