17.2 Elementares über differenzierbare Abbildungen

Beispiele.

1. Jede lineare Funktion $a$ ist differenzierbar mit $a'(x)=a$, denn es ist $a(x+v)-a(x)-a(v)=0$.
2. Es sei $f(x,y,z):=x\cdot y^2+\sin(z)$. Dann ist

   $$\frac{\d f(x,y,z)}{\d x}=\d _1 f(x,y,z) = y^2$$

   $$\frac{\d f(x,y,z)}{\d y}=\d _2 f(x,y,z) = 2xy$$

   $$\frac{\d f(x,y,z)}{\d z}=\d _3 f(x,y,z) = \cos(z)$$

   
   

3. Es sei $f(x,y):=\sin(2\varphi )$, wobei $(r,\varphi )$ die Polarkoordinaten von $(x,y)$ sind, und $f(0)=0$, d.h. $f(x,y)=2\sin(\varphi )\cos(\varphi )=\frac{2xy}{x^2+y^2}$ für $(x,y)\ne 0$, siehe (17.2.3). Dann ist $\d _1 f(0)=0=\d _2 f(0)$, aber $\d _{(1,1)}f(0)$ existiert nicht, da $t\mapsto f(t,t)$ unstetig ist bei 0. Insbesonders existiert also $f'(0)$ nicht.
4. Es sei

   $$f(x,y) :=r \sin(3\varphi )=r (\sin(\varphi ) \cos(2\varphi )+\cos(\varphi ) \sin(2\varphi ))$$

   $$= r^3(3\sin(\varphi )\cos(\varphi )^2-\sin(\varphi )^3)/r^2 =\frac{3x^2y-y^3}{x^2+y^2} = \frac{3x^2-y^2}{x^2+y^2} y.$$

   
   
   Beachte, daß $f$ 1-homogen ist und somit die Differenzenquotienten
   $$(f(tv)-f(0))/t=f(v)=d_vf(0)$$
   erfüllen. Es ist aber $f$ nicht linear, denn $f(1,0)=0$, $f(0,1)=-1$ aber $f(1,1)=1$, und somit existiert $f'(0)$ nicht. Wir können also in der Definition der Differenzierbarkeit die Linearität von $f'(x)$ nicht weglassen.

17.2.1 Lemma. Bilineare sind differenzierbar.
Es sei $f:E_1\times E_2\to F$ bilinear. Dann ist $f$ differenzierbar mit Ableitung

$$f'(x_1,x_2)(v_1,v_2) := f(v_1,x_2) + f(x_1,v_2).$$

Beispiele bilinearer Abbildungen sind:

1. Die Multiplikation $\mathbb{R}\times \mathbb{R}\to \mathbb{R}$, $(t,s)\mapsto ts$;
2. Die Skalarmultiplikation $\mathbb{R}\times E\to E$, $(t,v)\mapsto tv$;
3. Die Auswertung (oder Evaluation) $\operatorname{ev}:L(E,F)\times E\to F$, $(A,x)\mapsto A(x)$;
4. Die Komposition $\o :L(F,G)\times L(E,F)\to L(E,G)$, $(T,S)\mapsto T\o S$;
5. Die Determinante $\det:\mathbb{R}^2\times \mathbb{R}^2\to \mathbb{R}$;
6. Das Kreuzprodukt $\times :\mathbb{R}^3\times \mathbb{R}^3\to\mathbb{R}^3$;
7. Das innere Produkt $\langle\_\vert\_\rangle$ am $\mathbb{R}^n$, gegeben durch $\langle x\vert y\rangle=\sum_i x^i y^i$;

Beweis. Es ist

$$f\Bigl(\undersetbrace{=x}\to{(x_1,x_2)}+ \unde... ...\Bigl(\undersetbrace{=:a(v)}\to{f(x_1,v_2)+f(v_1,x_2)}\Bigr)=f(v_1,v_2)$$

und somit ist

$$\lim_{v\to 0}\frac{\vert f(x+v)-f(x)-a(v)\vert}{\vert v\vert}=\lim_{v\to 0}\frac{\vert f(v)\vert}{\vert v\vert} =0,$$

da $\vert f(v_1,v_1)\vert\leq \Vert f\Vert \Vert v_1\Vert \Vert v_2\Vert\leq \Vert f\Vert \Vert v\Vert^2$ wegen dem nachfolgenden Resultat.     []

17.2.2 Lemma. Bilineare versus lineare Abbildungen.
Es bezeichne $L(E_1,E_2;F)$ den Vektorraum der bilinearen Abbildungen $E_1\times E_2\to F$ versehen mit der Norm $\Vert f\Vert:=\sup\{\Vert f(x,y)\Vert:\Vert x\Vert\leq 1, \Vert y\Vert\leq 1\}$. Dann haben wir einen Isomorphismus

$$L(E_1,E_2;F)\cong L(E_1,L(E_2,F))$$

gegeben durch $f\mapsto \check f$, $\hat f \DOTSB\kern.2em\setbox0=\hbox{$\leftarrow$\kern-.15em\raise0.1ex\hbox{$\vert$}}\box0 \kern.3emf$.

Beweis. Dies folgt sofort aus

$$\Vert A\Vert = \sup\{\Vert A(x,y)\Vert:\Vert x\Vert\leq 1 \Vert y\Vert\leq 1\} = \sup\{\Vert\check A(x)(y)\Vert:\Vert x\Vert\leq 1 \Vert y\Vert\leq 1\}$$

$$= \sup\{\Vert\check A(x)\Vert:\Vert x\Vert\leq 1\} = \Vert\check A\Vert{\rm\quad[]}$$

17.2.3 Kettenregel.
Es sei $f:E\supseteq U\to F$ differenzierbar bei $x\in U$ und $g:F\supseteq V\to G$ differenzierbar bei $f(x)\in V$. Dann ist $g\o f:E\supseteq U\supseteq f^{-1}(V)\to V \to G$ differenzierbar bei $x$ und es gilt

$$(g\o f)'(x)= g'(f(x))\o f'(x).$$

Beweis. Es bezeichne

$$r_f(v) := f(x+v) - f(x) - f'(x)(v)$$

$$r_g(w) := g(f(x)+w) - g(f(x)) - g'(f(x))(w)$$

dann ist $\lim_{v\to 0}r_f(v)/\Vert v\Vert=0$ und $\lim_{w\to 0} r_g(w)/\Vert w\Vert=0$ und somit gilt für

$$r_{g\o f} (v) := (g\o f)(x+v) - (g\o f)(x) - \Bigl(g'(f(x))\o f'(x)\Bigr)(v)$$

$$= g'(f(x))\Bigl(f(x+v)-f(x)\Bigr) + r_g\Bigl(f(x+v)-f(x)\Bigr) - \Bigl(g'(f(x))\o f'(x)\Bigr)(v)$$

$$= g'(f(x))\Bigl(\underline{f'(x)(v)}+r_f(v)\Bigr) + r_g\Bigl(f'(x)(v)+r_f(v)\Bigr) - \underline{\Bigl(g'(f(x))\o f'(x)\Bigr)(v)}$$

$$= g'(f(x))(r_f(v)) + r_g\Bigl(f'(x)(v)+r_f(v)\Bigr)$$

die geforderte Eigenschaft:

$$\frac{\Vert r_{g\o f}(v)\Vert}{\Vert v\Vert} \leq \frac{\Vert g'(f(x))(r_f(v))\Vert}{\Vert v\Vert} + \frac{\Ve... ...Vert f'(x)(v)\Vert}{\Vert v\Vert}+\frac{\Vert r_f(v)\Vert}{\Vert v\Vert} \Bigr)$$

$$\leq \Vert g'(f(x))\Vert\cdot \frac{\Vert r_f(v)\Vert}{\Vert v\Ve... ...v)\Vert} \Bigl( \Vert f'(x)\Vert+\frac{\Vert r_f(v)\Vert}{\Vert v\Vert} \Bigr)$$

$$\to 0,$$

denn nach (16.3.2) ist $\vert a(x)\vert\leq \vert a\vert\cdot\vert x\vert$ für alle linearen $a$ wobei $\vert a\vert:=\sup\{\vert a(x)\vert:\vert x\vert\leq 1\}$.     []

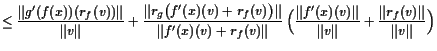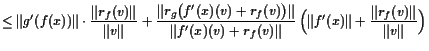Die Kettenregel stimmt auch für Richtungsableitungen, wenn die äußere Abbildung $g$ als differenzierbar vorausgesetzt wird.

17.2.4 Folgerung.
Falls $f:E\supseteq U\to F$ differenzierbar bei $x\in U$ und $a:F\to G$ linear ist, so ist $(a\o f)'(x)= a\o f'(x)$.    []

17.2.5 Lemma. Komponentenweise Ableitung.
Es sei $f=(f^1,\dots,f^m):E\supseteq U\to F_1\times \dots\times F_m$ und $x\in U$. Dann ist $f$ genau dann differenzierbar $x$, wenn die Komponenten $f^j:E\supseteq U\to F_j$ differenzierbar bei $x$ sind für alle $j$. Es gilt dann

$$f'(x)(v)=((f^1)'(x)(v),\dots,(f^m)'(x)(v)).$$

Wir sagen auch die Matrixdarstellung $[f'(x)]$ von $f'(x)$ ist

$$[f'(x)] = \left(\begin{matrix}(f^1)'(x) \vdots (f^m)'(x) \end{matrix}\right)$$

Beweis. $(\Rightarrow)$ Da $f^j:=\operatorname{pr}_j\o f$, wobei $\operatorname{pr}_j:F_1\times \dots\times F_m\to F_j$ die kanonische Projektion bezeichnet, folgt dies aus (17.2.4).

$(\Leftarrow)$ folgt, da das Restglied $r(h):=f(x+h)-f(x)-f'(x)(h)$ komponentenweise berechnet werden kann und Limiten in einem Produkt komponentenweise berechnet werden können.     []

17.2.6 Folgerung. Linearität des Differenzierens.
Es seien $f,g:E\supseteq U\to F$ differenzierbar bei $x\in U$ und $\lambda \in\mathbb{R}$, dann ist auch $f+\lambda g$ differenzierbar bei $x$ und es gilt $(f+\lambda g)'(x)=f'(x)+\lambda g'(x)$.

Beweis. Es ist $(f,g)\mapsto f+\lambda g$, $F\times F\to F$ stetig und linear und $(f,g):E\to F\times F$ differenzierbar mit Ableitung $(f,g)'(x)=(f'(x),g'(x))$.     []

17.2.7 Folgerung. Leibniz-Regel.
Es sei $b:F_1\times F_2\to F$ bilinear, sowie $f_j:E\supseteq U\to F_j$ differenzierbar, dann ist $b\o (f_1,f_2):E\supseteq U \to E$ differenzierbar und

$$(b\o (f_1,f_2))'(x)(h) = b(f_1'(x)(h),f_2(x)) + b(f_1(x),f_2'(x)(h)).{\rm\quad[]}$$

Ist insbesonders $b$ die Multiplikation von $\mathbb{R}$, so lautet diese Regel für $f_1,f_2:\mathbb{R}\to\mathbb{R}$:

$$(f_1\cdot f_2)'(x) = f_1'(x)\cdot f_2(x) + f_1(x)\cdot f_2'(x).$$

Ist $f_2(x)\ne 0$ so gilt auch

$$\left(\frac{f_1}{f_2}\right)'(x) = \frac{f_2(x) f_1'(x)-f_1(x) f_2'(x)}{f_2(x)^2},$$

denn nach (17.1.2) ist $\frac{d}{dx}\frac1{x}=-\frac1{x^2}$ und somit nach Kettenregel (17.2.3) $\frac{d}{dx}\frac1{f_2(x)}=-\frac1{f_2(x)^2} f_2'(x)$ und schlußendlich

$$\left(\frac{f_1}{f_2}\right)'(x) = \frac{d}{dx}f_1(x)\cdot \frac1{f_2(x)} + f_1(x)\cdot \frac{d}{dx}\frac1{f_2(x)} = \frac{f_1'(x)}{f_2(x)}-\frac{f_1(x) f_2'(x)}{f_2(x)^2}$$

$$= \frac{f_2(x) f_1'(x)-f_1(x) f_2'(x)}{f_2(x)^2}.$$

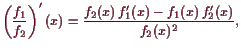
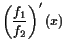17.2.8 Definition. Partielle Ableitungen.
Es sei $f:E_1\times \dots\times E_m\supseteq U\to F$ eine Abbildung und $x=(x^1,\dots,x^m)\in U$. Unter der $j$-ten partiellen Ableitung $\d _j f(x)$ von $f$ bei $x$ versteht man die Ableitung der Funktion $f\o\operatorname{ins}_j^x:E_j\supseteq (\operatorname{ins}_j^x)^{-1}(U)\to F$ bei $x^j$, wobei $\operatorname{ins}_j^x:E_j\to E_1\times \dots\times E_m$ gegeben ist durch $z\mapsto (x^1,\dots,x^{j-1},z,x^{j+1},\dots,x^m)$, d.h. $\operatorname{ins}_j^x$ ist affin mit linearen Teil $\operatorname{ins}_j:=\operatorname{ins}_j^0$ und konstanten Teil $(\dots,x^{j-1},0,x^{j+1},\dots)$. Vermöge einer Translation um $-x^j$ nach 0 können wir $\d _j f(x)$ auch als Ableitung von $(f\o (\operatorname{ins}_j+x))$ an der Stelle 0 definieren.

17.2.9 Folgerung.
Es sei $f:E_1\times \dots\times E_m\supseteq U\to F$ differenzierbar bei $x=(x^1,\dots,x^m)\in U$. Dann existieren alle partielle Ableitungen $\d _j f(x)$ für $j=1,\dots,m$ und es ist

$$f'(x)(h^1,\dots,h^m)=\sum_{j=1}^m \d _j f(x)(h^j).$$

Wir sagen auch die Matrixdarstellung $[f'(x)]$ von $f'(x)$ ist

$$[f'(x)] = (\d _1 f(x),\dots,\d _m f(x))$$

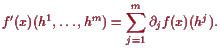
Beweis. Wegen der Kettenregel (17.2.3) ist

$$\d _j f(x^j)(h^j) = (f\o\operatorname{ins}_j^x)'(x^j)(h^j)$$

$$= \Bigl(f'(\operatorname{ins}_j^x(x^j))\o (\operatorname{ins}_j^x)'(x^j)\Bigr)(h^j) = f'(x)(\operatorname{ins}_j^x(h^j)),$$

denn die Ableitung der durch $h^j\mapsto (x^1,\dots,x^{j-1},h^j,x^{j+1},\dots,x^m)$ gegebenen affinen Funktion $\operatorname{ins}_j^x:E_j\to E_1\times \dots\times E_m$ ist der lineare Anteil

$$\operatorname{ins}_j:h^j\mapsto (0,\dots,0,h^j,0,\dots,0).{\rm\quad[]}$$

17.2.10 Folgerung. Jacobi-Matrix.
Es sei $f=(f^1,\dots,f^m): E_1\times \dots\times E_n\supseteq U\to F_1\times \dots\times F_m$ differenzierbar bei $(x_1,\dots,x_m)\in U$, dann existieren für alle $i$ und alle $j$ die partiellen Ableitungen $\d _i f^j$ der $j$-ten Komponente $f^j$ für alle $j$ und die Matrixdarstellung $[f'(x)]$ von $f'(x)$ ist gegeben durch

$$\left(\begin{matrix} \d _1 f^1 (x) & \hdots & ... ...dots \\ \d _1 f^m (x) & \hdots & \d _n f^m(x) \\ \end{matrix}\right),$$

d.h. für $v=(v^1,\dots,v^n)\in E_1\times \dots\times E_n$ ist

$$f'(x)(v) = \left(\begin{matrix} \d _1 f^1 (x)... ...ght) \cdot \left(\begin{matrix}v^1 \vdots v^n \end{matrix}\right)$$

Insbesonders heißt diese Matrix im Falle $E_j=\mathbb{R}=F_j$ für alle $j$ Jacobimatrix.

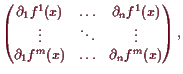
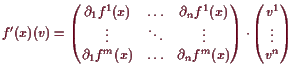
Beweis. Das Resultat folgt durch Anwenden von (17.2.5) und dann (17.2.10) auf jede der Komponenten $f^j$, denn

$$f'(x)(v) \ifpdf=\else\overset{\htmlref{(17.2.5)}{nmb:17.2.5}}{=}\fi ((f^1)'(x)(v),\dots, (f^m)'(x)(v))$$

$$\ifpdf=\else\overset{\htmlref{(17.2.10)}{nmb:17.2.10}}{=}\fi (\sum_i\d _if^1(x)(v^i),\dots,\sum_i \d _if^m(x)(v^i))$$

$$= \left(\begin{matrix}\d _1 f^1 (x) & \hdots & \d _n f^1(x) \v... ...\cdot \left(\begin{matrix}v^1 \vdots v^n \end{matrix}\right) {\rm\quad[]}$$

Beispiel (16.2.8) zeigt, daß aus der partiellen Differenzierbarkeit jedoch nicht die Differenzierbarkeit folgt.