17.3 Stetige Differenzierbarkeit

Wie wir in (17.1.3) gesehen haben, ist das Verschwinden der Ableitung $f'(x_0)$ eine notwendige Bedingung dafür, daß $x_0\in U$ ein Stelle ist, wo $f:E\supseteq U\to\mathbb{R}$ ein Minimum oder Maximum hat. Um allerdings entscheiden zu können, ob ein solches nun wirklich vorliegt wurde in der Schule die zweite Ableitung benutzt. Wir wollen nun den Weg ebnen höhere Ableitungen zu definieren. Gleichzeitig werden wir Bedingungen finden, die uns erlauben aus der Existenz der Richtungs- oder der partiellen Ableitungen auf die Differenzierbarkeit schließen zu können.

Falls $f:E\supseteq U\to F$ differenzierbar ist, so existiert für jeden Punkte $x\in U$ die Ableitung $f'(x)\in L(E,F)$ von $f$ bei $x$. Wir erhalten somit eine Abbildung

$$f':E\supseteq U\to L(E,F).$$

Unter der zweiten Ableitung werden wir in (19.1.1) (im wesentlichen) die Ableitung dieser Abbildung verstehen.

Wir müssen also von Differenzierbarkeit oder zumindest Stetigkeit von Abbildungen $g:E\supseteq U\to L(E,F)$ sprechen können. Da $E$ und $F$ als endlich dimensionale Vektorräume vorausgesetzt sind, ist auch die Menge $L(E,F)$ aller linearen Abbildungen von $E$ nach $F$ ebenfalls ein endlich dimensionaler Vektorraum nach (10.18) und mittels Basen von $E$ und $F$ können wir die Elemente von $L(E,F)$ mit $n\times m$-Matrizen identifizieren, wobei wir $n:=\dim(F)$ und $m:=\dim(E)$ gesetzt haben. Es ist also $L(E,F)$ isomorph zu $\mathbb{R}^{n\cdot m}$ und $g:E\supseteq U\to L(E,F)$ ist genau dann stetig, wenn alle Eintragungen $g_{i,j}(x)$ der Matrix $g(x)$ stetige Abbildungen $E\supseteq U\to\mathbb{R}$ liefern.

Üblicherweise verwenden wir auf $\mathbb{R}^{nm}$ die euklidische Metrik aus (15.2.2), d.h. die Distanz zweier linearer Abbildungen $A,B\in L(E,F)$ wäre durch

$$d(A,B):= \sqrt{\sum_{i=1}^n\sum_{j=1}^m (a_{i,j}-b_{i,j})^2}$$

gegeben, wobei $a_{i,j}$ und $b_{i,j}$ die Koeffizienten der Matrix $[A]$ und $[B]$ seien.

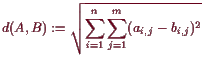
Besser mit der Wirkung von linearen Abbildungen auf Vektoren ist jedoch folgende Metrik auf $L(E,F)$ geeignet:

17.3.1 Definition. Stetig differenzierbar.
Es ist $d(A_0,A_1):=\Vert A_1-A_0\Vert$ mit $\Vert A\Vert:=\sup\{\vert A\cdot v\vert:\vert v\vert\leq 1\}$ gegeben. Dabei heißt $\Vert A\Vert$ die Operatornorm von $A$.

Beachte, daß für $A\in L(E,F)$ und $v\in V$ folgendes gilt:

$$\vert A\cdot v\vert \leq \vert A\vert\cdot \vert v\vert.$$

In der Tat ist $v=\vert v\vert\cdot v_1$ wobei $v_1:=\frac1{\vert v\vert} v$ Länge $1$ hat, also ist

$$\vert A\cdot v\vert=\vert A(\vert v\vert\cdot ... ...\vert v\vert\cdot \vert A(v_1)\vert\leq \vert v\vert\cdot \vert A\vert.$$

Es heißt $f:E\supseteq U\to F$ stetig differenzierbar (kurz $C^1$), falls $f'(x)$ für alle $x\in U$ existiert und $f':E\supseteq U\to L(E,F)$ stetig ist.

Da $\operatorname{ev}:L(E,F)\times E\to F$ bilinear und somit stetig ist ( $\Vert\operatorname{ev}(a,x)\Vert=\Vert a(x)\Vert\leq \Vert a\Vert\cdot\Vert x\Vert$) folgt aus der Stetigkeit von $f':U\to L(E,F)$ jene von $\widehat{f'}:U\times E\to L(E,F)\times E\to F$.

Für endlich dimensionales $E\cong \mathbb{R}^m$ gilt auch die Umkehrung, denn dann ist $L(E,F)\cong L(\mathbb{R}^m,F)\cong \mathbb{R}^m$ und aus der Stetigkeit von $\widehat{f'}:U\times E\to F$ folgt jene von $\operatorname{ev_{e_i}}\o f':U\to L(E,F)\to F$ und somit auch von $f':U\to F$ (punktweise Konvergenz).

17.3.2 Proposition. Differenzierbarkeit via Richtungsableitungen.
Eine Abbildung $f:E\supseteq U\to F$ ist genau dann $C^1$, wenn die Richtungsableitungen eine wohldefinierte und stetige Abbildung $E\supseteq U\to L(E,F)$, $x\mapsto (v\mapsto d_vf(x))$ liefern.

Beweis. $(\Rightarrow)$ Nach (17.1.9) existieren die Richtungsableitungen und $d_vf(x)=f'(x)$, also definieren sie gerade die Abbleitung $f':E\supseteq U\to L(E,F)$.

$(\Leftarrow)$ Wegen Proposition (17.1.9) müssen wir nur zeigen, daß

$$\frac{f(x+tv)-f(x)}{t} - f'(x)(v)\to 0$$ for $$t\to 0+$$ glm. für $$\Vert v\Vert=1.$$

Nach dem Mittelwertsatz (17.1.4) angewendet auf $c:s\mapsto f(x+sv)$ mit Ableitung $c'(s)= d_{v} f(x+sv)$ ist für eine $0<\vartheta<1$

$$\frac{f(x+tv)-f(x)}{t} = \frac1t(c(t)-c(0)) = c'(\vartheta t) = d_vf(x+\vartheta t v).$$

Wegen der vorausgesetzen Stetigkeit existiert für jedes $\varepsilon >0$ ein $\delta >0$, so daß für alle $\Vert w\Vert<\delta$ folgendes gilt: $\Vert d_vf(x+w)-d_vf(x)\Vert\leq \varepsilon \Vert v\Vert$. Für $\Vert v\Vert=1$ und $0<t<\delta$ erhalten wir also

$$\begin{multline*} \Bigl\Vert\frac{f(x+tv)-f(x)}{t} - f'(x)(v) \Bigr\Vert \leq \\... ...t v)-d_vf(x)\Vert:0<\vartheta<1\} \leq \varepsilon .{\rm\quad[]} \end{multline*}$$

17.3.3 Proposition. Differenzierbarkeit via partielle Ableitungen.
Ein Abbildung $f:E_1\times \dots\times E_m\supseteq U\to F$ ist genau dann stetig differenzierbar auf $U$, wenn sämtliche partielle Ableitungen $\d _jf:U\to L(E_j,F)$ für $j\in\{1,\dots,m\}$ existieren und stetig sind.

Beweis. $(\Rightarrow)$ Dies folgt aus (17.2.10), denn $\d _j f(x) = (f\o\operatorname{ins}_j^x)'(x^j)=f'(x)\o\ope... ...eratorname{ins}_j^*(f'(x)) =(\operatorname{ins}_j^*\o f')(x)\in L(E_j,F)$, und $(\operatorname{ins}_j^*):L(E_1\times \dots\times E_m,F)\to L(E_j,F)$ ist eine stetige Kontraktion.

$(\Leftarrow)$ Die wesentliche Beweis-Idee sieht man bereits im Fall $m=2$ und $E_1=E_2=F=\mathbb{R}$. Wir führen den Beweis also nur in dieser Situation. Beachte, daß dann $L(E_i,F)=L(\mathbb{R},\mathbb{R})\cong\mathbb{R}$ ist. Es genügt wegen (17.1.9) zu zeigen, daß $d_vf(x):=\lim_{t\to 0+}\frac{f(x+tv)-f(x)}{t}$ glm. für $\vert v\vert\leq 1$ existiert und $v\mapsto d_vf(x)$ für jedes $x\in U$ linear ist. O.B.d.A. sei $x=(0,0)$ und $v=(v_1,v_2)$. Dann ist

$$\frac{f(t v_1,t v_2) - f(0,0)}{t} = \frac{f(t... ..._2) - f(t v_1,0)}{t v_2} v_2 + \frac{f(t v_1,0)-f(0,0)}{t v_1} v_1.$$

Wegen dem Mittelwertsatz (17.1.4) angewendet auf $s\mapsto f(s,0)$ existiert zu $t$ und $v_1$ ein $\vartheta_1$ mit $0<\vartheta_1<1$ und

$$\frac{f(t v_1,0)-f(0,0)}{t v_1}=\d _1 f(\vartheta_1 tv_1,0).$$

Ebenso existiert wegen dem Mittelwertsatz angewendet auf $s\mapsto f(tv_1,s)$ zu $t$ und $v=(v_1,v_2)$ ein $\vartheta_2$ mit $0<\vartheta_2<1$ und

$$\frac{f(t v_1,t v_2)-f(t v_1,0)}{t v_2}=\d _2 f(t v_1,\vartheta_2 tv_2).$$

Insgesamt erhalten wir also

$$\frac{f(t v_1,t v_2) - f(0,0)}{t} =\d _2 f(t v_1,\vartheta_2 tv_2)\cdot v_2 + \d _1 f(\vartheta_1 tv_1,0)\cdot v_1$$

und wegen der Stetigkeit von $\d _1 f$ und $\d _2 f$ konvergiert dieser Ausdruck gleichmäßig für $\vert v\vert=\sqrt{\vert v_1\vert^2+\vert v_2\vert^2}\leq 1$ gegen

$$\d _1 f(0,0)\cdot v_1 + \d _2 f(0,0)\cdot v_2.$$

Da dieser Ausdruck offensichtlich linear in $v=(v_1,v_2)$ ist, ist $f$ differenzierbar nach (17.1.9) und $f'(x)(v)=\sum_i \d _i f(x) v_i$. Da $\d _i f$ stetig ist, ist es auch $f'$, also ist $f$ stetig differenzierbar.     []

17.3.4. Inverse Funktionen Wir wollen nun Gleichungen der Form $f(x)=y$ nach $x$ auflösen. Sei also $g(y):=x$ eine Lösung. Falls nicht nur $f$ sondern auch $g$ differenzierbar ist, so gilt wegen $f(g(y))=y$ nach der Kettenregel (17.2.3) $f'(g(y))\cdot g'(y)=\operatorname{id}$. Wenn die Lösungen eindeutig sind, d.h. $f$ injektiv ist, dann ist wegen $f(g(f(x)))=f(x)$ auch $g(f(x))=x$ also $g'(f(x))\cdot f'(x)=\operatorname{id}$ und speziell für $x=g(y)$ ist $g'(y)\cdot f'(g(y))=\operatorname{id}$, d.h. $g'(y)$ ist die inverse (lineare Abbildung) zu $f'(g(y))$.

Im endlich dimensionalen können wir die Invertierbarkeit linearer Abbildungen mit der Determinante testen, siehe (12.20).

Die Idee des folgenden Satzes ist, daß, wenn die Gleichung $f'(x_0)(x)=y$ die durch die lineare Approximation $f'(x_0)$ gegeben ist, eindeutig für alle $y$ lösbar ist, dann sollte auch die nicht-lineare Gleichung $f(x)=y$ zumindest für $y$ nahe $f(x_0)$ eindeutig mit $x$ nahe $x_0$ lösbar sein.

Satz über inverse Funktionen.
Es sei $f:E\supseteq U\to F$ $C^1$, $x_0\in U$ und $f'(x_0):E\to F$ ein Isomorphismus. Dann ist $f$ ein lokaler Diffeomorphismus, d.h. es gibt offene Umgebungen $V\subseteq U$ von $x_0$ und $W$ von $f(x_0)$ so daß $f:V\to W$ bijektiv ist und die Inverse $f^{-1}:W\to V$ $C^1$ ist mit Ableitung $(f^{-1})'(y)=f'(f^{-1}(y))^{-1}$.

Eine Menge $U\subseteq E$ heißt offene Umgebung von $x_0\in E$, wenn $U$ offen ist und $x_0\in U$ liegt.

Beweis. Zuerst vereinfachen wir das Problem. Durch eine Translation (wir ersetzen $f$ durch $x\mapsto f(x_0+x)-f(x_0)$) erreichen wir $x_0=0$ und $f(x_0)=0$. Durch Zusammensetzen mit $f'(x_0)^{-1}$ erreichen wir $f'(x_0)=\operatorname{id}$. Da die lineare Approximation $\operatorname{id}$ von $f$ invertierbar ist, sollten wir das Restglied

$$r(x) := f(x_0+x) - f(x_0) - f'(x_0)(x) = f(x) - x$$

betrachten. Es ist $r(0)=0$ und $r'(0)=f'(0)-\operatorname{id}=0$, also existiert ein $\delta >0$ mit $\Vert x\Vert\leq \delta \Rightarrow x\in U$ und $\Vert f'(x)-\operatorname{id}\Vert=\Vert r'(x)\Vert\leq 1/2$. Somit ist nach dem Mittelwertsatz (17.1.4)

$$\Vert r(x_1)-r(x_2)\Vert \leq \max\bigl\{\Vert r'(x_2+t(x_1-x_2))(x_2-x_1)\Vert\bigr\} \leq \frac12\Vert x_1-x_2\Vert$$

für $\Vert x_j\Vert\leq \delta$. Speziell für $x_0:=0$ erhalten wir $\Vert r(x)\Vert\leq \Vert x\Vert/2$ für $\Vert x\Vert\leq \delta$. Wir behaupten nun, daß für alle $\Vert y\Vert< \delta /2$ ein eindeutiges $\Vert x\Vert<\delta$ mit $f(x)=y$ existiert. Dazu wandeln wir diese Gleichung in die Fixpunktgleichung $x=g_y(x):=y+x-f(x)=y-r(x)$ um. Für $\Vert y\Vert< \delta /2$ und $\Vert x\Vert\leq \delta$ ist $\Vert g_y(x)\Vert\leq \Vert y\Vert+\Vert r(x)\Vert< \delta /2 + \Vert x\Vert/2\leq \delta$ und weiters ist $\Vert g_y(x_1)-g_y(x_2)\Vert= \Vert r(x_1)-r(x_2)\Vert\leq \Vert x_1-x_2\Vert/2$. Also folgt aus dem Banach'schen Fixpunktsatz (16.4.6) die Existenz eines eindeutig bestimmten Fixpunktes $\Vert x\Vert\leq \delta$ und wegen $\Vert x\Vert=\Vert g_y(x)\Vert<\delta$ liegt dieser im Inneren.

Es sei nun $W:=\{y:\Vert y\Vert<\delta /2\}$ und $V:=f^{-1}(W)\cap\{x:\Vert x\Vert<\delta \}$. Dann existiert für jedes $y\in W$ ein eindeutiges $\Vert x\Vert<\delta$ mit $f(x)=y$, also liegt $x\in V$ und $f:V\to W$ ist bijektiv.

Es ist $f^{-1}$ (Lipschitz-)stetig, denn für $y_j\in W$ und $x_j\in V$ mit $f(x_j)=y_j$ gilt: $\Vert x_1-x_2\Vert \leq \Vert f(x_1)-f(x_2)\Vert + \Vert r(x_1)-r(x_2)\Vert \leq \Vert y_1-y_2 \Vert + \frac12\Vert x_1-x_2\Vert$, also $\Vert x_1-x_2\Vert \leq 2 \Vert y_1-y_2\Vert$.
Und schließlich ist $f^{-1}$ differenzierbar, denn

$$\bigl\Vert f^{-1}(y_1) - f^{-1}(y_2) - f'(x_2)^{-1}(y_1-y_2)\bigr\Vert = \bigl\Vert x_1-x_2-f'(x_2)^{-1}(f(x_1)-f(x_2)) \bigr\Vert$$

$$\leq \Vert f'(x_2)^{-1}\Vert\cdot \undersetbrace {\to 0}\to {\fra... ...2\Vert}} \cdot \undersetbrace{\leq 2\Vert y_1-y_2\Vert}\to{\Vert x_1-x_2\Vert}.$$

Beachte dabei, daß $f'(x_2)^{-1}$ existiert und mittels geometrischer Reihe berechnet werden kann, da $\Vert f'(x_2)-\operatorname{id}\Vert<1$.

Daß $f^{-1}$ $C^1$ ist folgt, da $(f^{-1})' = \operatorname{inv}\o f'\o f^{-1}$ und alle Komponenten stetig sind.     []

17.3.5 Beispiele inverser Abbildungen.

1. Es ist $\sin:[-\pi/2,\pi/2]\to [-1,1]$ streng monoton wachsend mit Ableitung $\sin'(x)=\cos(x)>0$ für $-\pi/2<x<\pi/2$. Also existiert für $\vert y\vert<1$ nach dem inversen Funktionensatz die Ableitung der Umkehrfunktion $\arcsin:[-1,1]\to[-\pi/2,\pi/2]$ bei $y$ und zwar ist

   $$\arcsin'(y) = \frac1{\sin'(\arcsin(y))}=\frac1{\cos(\arcsin(y))}$$

   $$=\frac1{\sqrt{1-\sin(\arcsin(y))^2}} =\frac1{\sqrt{1-y^2}}.$$

   
   
   

   Beachte, daß $\arcsin$ nur auf dem Bild $\sin(\mathbb{R})=[-1,1]$ definierbar ist, und $x=\arcsin(y)$ nur eine (die absolut kleinste) Lösung von $\sin(x)=y$ liefert.

   Analog zeigt man für $\cos:[0,\pi]\to[-1,1]$, daß $\arccos'(y)=-\frac1{\sqrt{1-y^2}}$ ist. Wieder ist $\arccos$ nur auf dem Bild $\cos(\mathbb{R})=[-1,1]$ definiert und $x=\arccos(y)$ ist die kleinste positive Lösung von $\cos(x)=y$.

   

2. Es ist $\tan:(-\pi/4,\pi/4)\to \mathbb{R}$ streng monoton wachsend mit Ableitung

   $$\tan'(x) =\frac{\cos(x)\sin'(x)-\sin(x)\cos'(x)}{\cos(x)^2} =\frac{\cos(x)^2+\sin(x)^2}{\cos(x)^2}$$

   $$=1+\tan(x)^2=\frac1{\cos(x)^2}\geq 1$$

   
   
   für alle $x$. Also existiert nach dem inversen Funktionensatz die Ableitung der Umkehrfunktion $\arctan$ und zwar ist
   $$\arctan'(y) = \frac1{\tan'(\arctan(y))}=\frac1{1+\tan(\arctan(y))^2} =\frac1{1+y^2}.$$

   Im Unterschied zu den vorigen Beispiel ist diese Umkehrfunktion nun auf $\mathbb{R}=\operatorname{Bild}(\tan)$ definiert und $x=\arctan(y)$ ist wieder nur eine Lösung diesmal von $\tan(x)=y$.

   

3. Nachtrag zu (16.2.1): Wir haben in (3.11) $a^n$ für $n\in\mathbb{N}$ und $a^{-1}=1/a$ für $a\ne 0$ definiert. Wegen (3.12) setzt man $a^{-n}:=1/a^n$ für $n\in\mathbb{N}$ und $a\ne 0$. Nach (6.7) existiert für $a>0$ und $0<m\in\mathbb{N}$ die m-te Wurzel $\root{m}\of{a}$ und wieder wegen (3.12) setzt man $a^{1/m}:=\root{m}\of{a}$ und schließlich
   $$a^x:= a^{\frac{p}q}=\root{q}\of{a^p}=\root{q}\of{a}^p$$    für $$x=\frac{p}{q}\in\mathbb{Q}$$ und $$a>0.$$
   Man kann zeigen, daß die Funktion $x\mapsto a^x$, $\mathbb{Q}\to\mathbb{R}$ eine stetige Fortsetzung zu eine Funktion $\mathbb{R}\to\mathbb{R}$ besitzt. Insbesonders für $a:=e$ heißt diese stetige und streng monoton wachsende Funktion Exponentialfunktion $\exp:x\mapsto x=e^x$.

   Wegen $\lim_{n\to{\infty}}e^n=+{\infty}$ und somit $\lim_{n\to{\infty}}e^{-n}=0$ ist $\exp:\mathbb{R}\to (0,+{\infty})$ bijektiv und folglich existiert nach (16.4.4) die Umkehrfunktion $\exp^{-1}:(0,+{\infty})\to\mathbb{R}$. Diese heißt natürlicher Logarithmus, wird mit $\operatorname{ln}$ oder $\log$ (in MATHEMATICA mit Log) bezeichnet und ist ebenfalls stetig und streng monoton wachsend. Wegen $\exp(x_1+x_2)=e^{x_1+x_2}=e^{x_1}\cdot e^{x_1}=\exp(x_1)\cdot \exp(x_2)$ ist $\operatorname{ln}(y_1\cdot y_2)=\operatorname{ln}(y_1)+\operatorname{ln}(y_2)$. Als nächstes wollen wir die Differenzierbarkeit von $\operatorname{ln}$ beweisen. Aus $e=\lim_{n\to{\infty}}(1+\frac1n)^n$ folgt durch Logarithmieren (d.h. Anwenden von $\operatorname{ln}$) $1=\operatorname{ln}(\exp(1))=\operatorname{ln}(e)=\operatorname{ln}(\lim_{n\to{\infty}}(1+\frac1n)^n)=\lim_{n\to {\infty}} n\operatorname{ln}(1+\frac1n)$. Und man kann dies verallgemeinern zu

   $$\operatorname{ln}'(1)=\lim_{t\to 0}\frac{\operatorname{ln}(1+t)-\operatorname{ln}(1)}{t} = \lim_{n\to{\infty}} n\operatorname{ln}(1+\frac1n)=1.$$
   Damit ist aber auch $\exp$ differenzierbar bei 0 mit Ableitung
   $$\exp'(0)=\lim_{s\to 0}\frac{\exp(s)-\exp(0)}{s}=\lim_{s\to 0}\frac{e^s-1}{s}$$
   und wenn wir $t=e^s-1$ setzten, dann ist $s\to 0$ äquivalent mit $t\to 0$, denn $s=\operatorname{ln}(t+1)$, und somit ist
   $$\exp'(0)=\lim_{s\to 0}\frac{e^s-1}{s}=\lim_{t\to 0}\frac{t}{\operatorname{ln}(1+t)}=1.$$
   Wegen $\exp(t+x)\exp(t)\exp(x)$ folgt schließlich

   $$\exp'(x) =\lim_{t\to 0}\frac{\exp(t+x)-\exp(x)}{t} =\lim_{t\to 0}\frac{e^t-1}{t} e^x$$

   $$=\exp'(1)\cdot \exp(x)=\exp(x).$$

   
   
   Nach dem inversen Funktionensatz existiert somit die Ableitung der Umkehrfunktion $\operatorname{ln}$ und zwar ist
   $$\operatorname{ln}'(y) = \frac1{\exp'(\operatorname{ln}(y))}=\frac1{\exp(\operatorname{ln}(y))} =\frac1y.$$
   

4. Quadrieren: Es sei $f:\mathbb{C}\to\mathbb{C}$ geben durch $f(z):=z^2$. Also ist $f$ als Abbildung von $\mathbb{R}^2\cong\mathbb{C}$ gegeben durch $f(x,y)=(x^2-y^2,2xy)$. Die Jacobimatrix von $f$ ist somit
   $$[f'(x,y)]=\begin{pmatrix}2x & -2y 2y & 2x \end{pmatrix}$$
   mit Determinante $\det(f'(x,y))=4(x^2+y^2)\ne 0$ für $(x,y)\ne(0,0)$. Nach den inversen Funktionensatz existiert somit lokal um Punkte $\ne 0$ die (eindeutig bestimmte) Umkehrfunktion $\sqrt{\quad}$. Global ist jedoch zu jeder Lösung $z$ von $z^2=w$ auch $-z$ eine weitere Lösung.
   

5. Polarkoordinaten:
   Es sei $f:\mathbb{R}^2\supseteq \mathbb{R}_+\times \mathbb{R}\to \mathbb{R}^2$, $(r,\varphi )\mapsto (r \cos(\varphi ),r \sin(\varphi ))$. Dann ist $f$ $C^1$ und
   $$f'(r,\varphi ) = \left(\begin{matrix}\cos(\varphi ) & -r \sin(\varphi ) \sin(\varphi ) & r \cos(\varphi ) \end{matrix}\right)$$
   invertierbar, da $\det(f'(r,\varphi ))=r>0$, aber
   $$f(r,\varphi +2 k \pi) = f(r,\varphi )$$ für alle $$k\in\mathbb{Z}.$$
   Also ist $f$ nicht global injektiv, vergleiche das mit dem 1-dimensionalen Inversen-Funktionenen Satz (17.1.8).
   

   Betrachten wir die modifizierte Abbildung

   $$f:\mathbb{R}^2\to\mathbb{R}^2,\qquad (s,\varphi )\mapsto (e^s \cos(\varphi ),e^s \sin(\varphi )),$$
   so ist
   $$f'(s,\varphi ) = \left(\begin{matrix}\cos(\varphi ) & -e^s \sin... ...{matrix}\right) \cdot \left(\begin{matrix}e^s & 0 0 & 1 \end{matrix}\right)$$
   und somit $\det(f'(s,\varphi ))=e^s\cdot e^s=e^{2s}>0$ für alle $s$. Dennoch ist $f$ nicht injektiv.
6. Ähnliches gilt auch für Kugelkoordinaten
   $$f:(r,\varphi ,\theta)\mapsto r(\cos(\theta) \cos(\varphi ),\cos(\theta) \sin(\varphi ),\sin(\theta))$$
   mit Jacobimatrix
   $$\begin{pmatrix} \cos(\theta) \cos(\varphi ) & -r \cos(\theta) ... ...theta) \sin(\varphi ) \\ \sin(\theta) & 0 & r \cos(\theta) \\ \end{pmatrix}$$
   und Determinante

   $$\det(f'(r,\varphi ,\theta)) = \sin(\theta) r^2 \sin(\theta) \cos(\theta) (\sin(\varphi )^2+\cos(\varphi )^2) +$$

   $$\quad + r \cos(\theta) r \cos(\theta)^2 (\sin(\varphi )^2+\cos(\varphi )^2)$$

   $$= r^2 \cos(\theta)\ne 0,$$

   
   
   falls $-\pi/2<\theta<\pi/2$ und $r\ne 0$. Folglich existiert eine stetig differenzierbare Umkehrfunktion.
7. Es sei $f:\mathbb{R}^2\to\mathbb{R}^2$ gegeben durch
   $$f(x,y)=(\sin(x) - \cos(y),\sin(y) - \cos(x))$$
   mit Jacobimatrix
   $$\begin{pmatrix} \cos(x) & \sin(y) \\ \sin(x) & \cos(y) \end{pmatrix}$$
   und Determinante $\cos(x) \cos(y)-\sin(x) \sin(y)=\cos(x-y)$. Dies ist $\ne 0$ falls $x$ nahe $y$ liegt. Folglich gibt es lokale $C^1$-Lösungen.
   

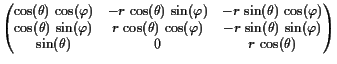
17.3.6. Nun geht es uns darum soetwas wie die Niveau-Linien

$$\{(x,y):f(x,y)=z\}$$

eines Gebirges $f:\mathbb{R}^2\to\mathbb{R}$ zu diskutieren, oder wenn wir $f$ als Luftdruck interpretieren die Isobaren oder als Temperatur die Isothermen. Wir versuchen dazu bei vorgegebenen $z$ die Lösungen $(x,y)$ von $f(x,y)=z$ mittels Funktionen $x\mapsto y$ zu beschreiben.

Satz über implizite Funktionen.
Es sei $f:E\times F\to F$ lokal um $(x_0,y_0)$ $C^1$ und $\d _2 f(x_0,y_0):F\to F$ ein Isomorphismus. Dann existieren offene Umgebungen $U$ von $x_0$, $V$ von $y_0$ und $W$ von $f(x_0,y_0)$, so daß für jedes $z\in W$ und $x\in U$ ein eindeutiges $y\in V$ existiert mit $f(x,y)=z$. Weiters ist die Abbildung $(x,z)\mapsto y$, $U\times W\to V$ $C^1$.

Beachte, daß wir die Ableitungen von $h:(x,z)\mapsto y$ durch Differenzieren der Gleichung $f(x,y)=z$ unter Anwendung der Kettenregel errechnet werden können, denn $\frac{\d }{\d x}$ liefert $\d _1 f(x,h(x,z))+\d _2f(x,h(x,z)) \d _1 h(x,z)=0$ und $\frac{\d }{\d z}$ liefert $\d _1 f(x,h(x,z))\cdot 0 +\d _2f(x,h(x,z)) \d _2 h(x,z)=\operatorname{id}$.

Beweis. Es sei $g:E\times F\to E\times F$ gegeben durch $(x,y)\mapsto (x,f(x,y))$. Dann ist

$$g'(x,y) = \left(\begin{matrix}1 & 0 \d _1f(x,y) & \d _2f(x,y) \end{matrix}\right)$$

invertierbar mit Inverser

$$\left(\begin{matrix} 1 & 0 \\ -\d _2f(x,y)^{-1}\cdot \d _1f(x,y) & \d _2f(x,y)^{-1} \end{matrix}\right),$$

(Man erhält dies durch einen allgemeinen Ansatz), also existieren nach dem Inversen-Funktionen Satz Umgebungen $U$, $V$ und $O$ von $x_0$, $y_0$ und $g(x_0,y_0)$, so daß $g:U\times V\to O$ ein Diffeomorphismus ist.

Nun wähle Umgebungen $U_1$ von $x_0$ und $W$ von $f(x_0,y_0)$ mit $U_1\times W\subseteq O$. Dann ist für jedes $x\in U_1$ und $z\in W$ der Punkt $(x,z)\in O$, also existiert ein eindeutiger Punkt $(u,y)\in U\times V$ mit $(x,z)=g(u,y)=(u,f(u,y))$, d.h. $u=x\in U_1$ und $f(x,y)=z$, also ein eindeutiger Punkt $y\in V$ mit $f(x,y)=z$. Weiters ist $(x,z)\mapsto y$ durch $(u,y)=g^{-1}(x,z)=:(h^1(x,z),h^2(x,z))$ gegeben, wobei $h^j$ die Komponenten von $g^{-1}$ bezeichnet. Folglich ist diese Zuordnung $C^1$.     []

17.3.7 Beispiele implizit gegebener Funktionen.

1. Kreisgleichung: $x^2+y^2=1$, d.h. die Lösungsmenge der impliziten Gleichung $f(x,y):=x^2+y^2=1$. Die Ableitung von $f$ ist $f'(x,y)=(2x,2y)$ d.h. für $y_0\ne 0$ ist $y$ lokal um $y_0$ nach $x$ auflösbar und für $x_0\ne 0$ ist $x$ lokal um $x_0$ nach $y$ auflösbar. Wir können dies sogar explizit machen: $y=\pm\sqrt{1-x^2}$ bzw. $x=\pm\sqrt{1-y^2}$.
   

2. Das kartesische Blatt ist durch $x^3+y^3=3xy$ gegeben, d.h. als Lösung der impliziten Gleichung $f(x,y):=x^3+y^3-3xy=0$. Die Ableitung von $f$ ist $f'(x,y)=(3(x^2-y),3(y^2-x))$, also ist nach dem impliziten Funktionensatz $y$ lokal um $y_0$ nach $x$ auflösbar falls $y_0^2\ne x_0$ oder $x_0^2\ne y_0$. Falls ein Punkt $(x_0,y_0)$ mit $y_0^2=x_0$ und $x_0^2=y_0$ die implizite Gleichung erfült, so gilt $x_0^4=x_0$, d.h. $x_0=0=y_0$ (oder $x_0=1=y_0$, aber das erfüllt nicht die Gleichung $0=f(x_0,y_0)=1^3+1^3-3=-1$.
   

   Ohne die Lösungskurve $x\mapsto y(x)$ explizit zu kennen, können wir durch Differenzieren der impliziten Gleichung $0=f(x,y(x))$ dennoch deren Ableitung berechnen:

   $$=\d _1 f(x,y(x)) + \d _2 f(x,y(x)) y'(x)$$ 0

   $$=3x^2 -3y(x) + (3y(x)^2-3x) y'(x) \Rightarrow$$

   $$y'(x) =\frac{y(x)-x^2}{y(x)^2-x}.$$

   
   

3. Es sei ein Polynom $p(t,x):=x^n+a_{n-1}(t) x^{n-1}+\dots+a_1(t) x+a_0(t)$ mit variable Koeffizienten $a_{n-1}(t)$,...,$a_0(t)$ gegeben. Angenommen wir kennen für $t=0$ eine Nullstelle $x_0$ von $p$, d.h. $p(0,x_0)=0$. Wir wüßten gerne, daß für alle kleinen $t$ auch Nullstellen $x_t$ die nahe $x_0$ liegen existieren, d.h. wir wollen in $p(t,x)=0$ die Variable $x$ nach $t$ auflösen. Falls $\d _2 p(0,x_0)\ne 0$ ist so geht dies auf stetig differenzierbare Weise wegen dem impliziten Funktionensatz. Es bedeutet $0=\d _2 p(0,x_0)$ gerade, daß $x_0$ keine Mehrfachnullstelle ist.
   

4. Es ist die Menge der Lösungen der impliziten Gleichung $f(x,y,z):=z^2+(\sqrt{x^2+y^2}-5)^2=4^2$ gesucht, ein sogenannter Torus. Die Ableitung ist
   $$f'(x,y,z)= \Bigl( 2(\sqrt{x^2+y^2}-5)\frac{x}{\sqrt{x^2+y^2}}, 2(\sqrt{x^2+y^2}-5)\frac{y}{\sqrt{x^2+y^2}},2z\Bigr)$$
   Für $z_0\ne 0$ ist also $z$ nahe $z_0$ eindeutig aus $(x,y)$ berechenbar, beschreibt also eine Fläche im $\mathbb{R}^3$. Ist andererseits $z_0=0$ und $f(x_0,y_0,z_0)=0$, so ist $\sqrt{x_0^2+y_0^2}=5\pm2\ne 0$ und somit $f'(x,y,z)\ne (0,0,0)$ also sicher eine der 3 Variablen aus den anderen beiden auf $C^1$-Weise berechenbar.
   

5. Es ist die Schnittmenge 2 normal aufeinander stehende Zylinder, deren Achsen sich nicht treffen, zu bestimmen.
   

   Der 1. Zylinder ist z.B. durch $(x+1)^2+y^2=4$ gegeben und der 2. Zylinder durch $(x-1)^2+z^2=4$. Gesucht sind also die Lösungen der impliziten Gleichung $f(x,y,z):=((x+1)^2+y^2,(x-1)^2+z^2)=(4,4)$. Die Ableitung von $f$ ist

   $$f'(x,y,z) = \begin{pmatrix}2x+2 & 2y & 0 2x-2 & 0 & 2z \end{pmatrix}.$$
   Wir fassen $f$ als Abbildung $f:\mathbb{R}\times \mathbb{R}^2\to\mathbb{R}^2$ auf. Dann ist $\d _2 f(x,y,z)=\begin{pmatrix}2y & 0 0 & 2z \end{pmatrix}$ genau dann invertierbar, wenn $yz\ne 0$ ist. Andererseits folgt aus $y=0$, daß $(x+1)^2=4$, d.h. $x=-1\pm 2$ und somit ist wegen $(x-1)^2+z^2=4$ im $+$-Fall $z=\pm 2$ und sonst existiert kein passendes $z$. Aus $z=0$ folgt hingegen, daß $(x-1)^2=4$, d.h. $x=1\pm 2$ ist und somit ist wegen $(x+1)^2+y^2=4$ im $-$-Fall $y=\pm 2$ und sonst existiert kein passendes $y$. D.h. abgesehen von den 4 Punkten $(1,0,\pm 2)$ und $(-1,\pm 2,0)$ ist also $y$ und $z$ lokal eindeutig aus $x$ ausrechenbar.

6. Wir wollen nun die Differenzierbarkeit der Abbildung $\iota :A\mapsto A^{-1}$ von $GL(E):=\{A\in L(E,E):A$ ist invertierbar $\}$ nach $GL(E)$ beweisen. Es ist $A^{-1}$ durch die Gleichung $A\o A^{-1}=\operatorname{id}_E$ gegeben, also $\iota$ durch die implizite Gleichung $\mu(A,\iota (A))=\operatorname{id}_E$ wobei $\mu:L(E,E)\times L(E,E)\to L(E,E)$ die Komposition ist. Da $\mu$ bilinear ist, ist $\d _2\mu (A,B)(C)=\mu(A,C)$ und somit ist $\d _2\mu(A,B)$ invertierbar mit inverser $C\mapsto \mu(A^{-1},C)$. Nach dem impliziten Funktionensatz ist also $\iota :GL(E)\to GL(E)$ differenzierbar mit Ableitung
   $$\iota '(A)(B)=-\Bigl(\bigl(\d _2\mu(A,\iota (A))\bigr)^{-1}\o\bigl(\d _1\mu(A,\iota (A))\bigr)\Bigr)(B) =-A^{-1}\o B\o A^{-1}.$$
   Vergleiche dies mit der Ableitung von $x\mapsto x^{-1}$, $\mathbb{R}\to\mathbb{R}$.

17.3.8. Newtonverfahren Um eine Nullstelle der (nicht-linearen) Gleichung $f(x)=0$ zu erhalten beginnen wir mit irgend einem Näherungswert $x_0$, betrachten die affine Funktion $x\mapsto f'(x_0)(x-x_0)+f(x_0)$ die $f$ am besten approximiert, bestimmen ihre Nullstelle $x_1$, d.h. lösen $f'(x_0)(x_1-x_0)+f(x_0)=0$ und erhalten als neue Näherungsnullstelle von $f$ den Punkt $x_1:=x_0-f'(x_0)^{-1} f(x_0)$. Das Newtonverfahren besteht nun darin auf rekursive Weise $x_{n+1}:=g(x_n):=x_n-f'(x_n)^{-1} f(x_n)$ zu definieren und zu hoffen, daß $x_{\infty}:=\lim_{n\to{\infty}}x_n$ existiert, weil dann $x_{\infty}=g(x_{\infty})$, also $f(x_{\infty})=0$ ist (Verwende die stetige Differenzierbarkeit von $f$ und damit die Stetigkeit von $g$). Da aber die Bestimmung der Inversen $f'(x_0)^{-1}$ einer Matrix $f'(x_0)$ sehr aufwendig ist, modifizieren wir dieses Verfahren derart, daß wir Anstelle von $f'(x_n)$ immer das fixe $f'(x_0)$ verwenden und erhalten:

Vereinfachtes Newtonverfahren.
Es sei $f:E\to F$ stetig differenzierbar und $x_0\in E$. Es sei $f'(x_0)$ invertierbar und es existiere ein $q<1$ mit $\vert f'(x_0)^{-1}\vert\cdot\vert f'(x_0)-f'(x)\vert\leq q$ für alle $x$ in einer offenen Menge $U$. Weiters sei

$$B:=\Bigl\{x:\vert x-x_0\vert\leq\frac{\vert f'(x_0)^{-1}\cdot f(x_0)\vert}{1-q}\Bigr\}\subseteq U.$$

Dann konvergiert die vereinfachte Newtonfolge $x_{n+1}:=x_n-f'(x_0)^{-1}\cdot f(x_n)$ gegen eine Nullstelle $\xi \in B$.

Beweis. Wir betrachten $g(x):=x-f'(x_0)^{-1}\cdot f(x)$. Für $x,y\in B$ ist nach dem Mittelwertsatz $\vert g(x)-g(y)\vert\leq \sup\{\vert g'(\xi )\vert \vert x-y\vert:\xi \in B\}$. Es ist

$$g'(z)=\operatorname{id}- f'(x_0)^{-1} f'(z) = f'(x_0)^{-1} (f'(x_0)-f'(z))$$

und somit

$$\vert g'(z)\vert\leq \vert f'(x_0)^{-1}\vert \vert f'(x_0)-f'(z)\Vert\leq q<1.$$

Nach Aufgabe (105) ist $g(B)\subseteq B$, da $B=\{x:d(x,x_0)\leq \frac{d(g(x_0),x_0)}{1-q}\}$. Nach dem Banach'schen Fixpunktsatz (16.4.6) existiert somit $x_{\infty}:=\lim_{n\to{\infty}} x_n\in B$ und somit ist $x_{\infty}=g(x_{\infty})=x_{\infty}-f'(x_0)^{-1}\cdot f(x_{\infty})$, also ist $f(x_{\infty})=0$.     []

17.3.9 Beispiel. Julia-Menge.
Die Menge der Startwerte, für welche die Newtonfolge gegen eine fixe Nullstelle konvergiert, ist im allgemeinen schwer beschreibbar. Betrachten wir z.B. das Polynom $p(z):=z^3-1$ als Abbildung $p:\mathbb{C}\to\mathbb{C}$. Dieses hat 3 komplexe Nullstellen $1$, $-\frac12\pm i \frac{\sqrt{3}}2$. Wir können es auch als Abbildung $p:\mathbb{R}^2\to\mathbb{R}^2$ auffassen. Die Ableitung von $p$ ist gegeben durch (Multiplikation mit) $3z^2$ und die Newtonrekursion somit durch $g:z\mapsto z-\frac{p(z)}{p'(z)}=z-\frac{z^3-1}{3z^2}=\frac{2z^3+1}{3z^2}$. Färben wir die Punkte der Ebene in 3 Farben entsprechend den 3 Nullstellen gegen welche die Newtonfolge mit diesen Startwerten konvergiert so erhalten wir folgendes fraktales Bild, eine Juliamenge:

Wir werden später sehen, daß für die Konvergenz der allgemeinen Newtonfolge die Bedingungen $\vert f'(z)^{-1}\vert^2 \vert f''(z)\vert \vert f(z)\vert\leq q<1$ und $\vert f'(z)^{-1} f(z)\vert\leq (1-q) r$ für alle $\vert z-z_0\vert\leq r$ genügen. In diesen Beispiel sind diese Bedingungen für $q:=1/2$ und $r:=1/2$ erfüllt.