19.1 Grundlegendes

19.1.1 Definition. Zweite Ableitung.
Wir wollen nun die 2. Ableitung einer Funktion $f:E\supseteq U\to F$ definieren. Für $x\in U$ war die Ableitung von $f$ bei $x$ eine lineare Abbildung $f'(x):E\to F$ (also $f'(x)\in L(E,F)$) und bei variierendem $x\in U$ ist für differenzierbares $f$ die Ableitung eine Abbildung $f':E\supseteq U\to L(E,F)$. Falls dies im Punkte $x\in U$ seinerseits differenzierbar ist, also $(f')'(x):E\to L(E,F)$ als lineare Abbildung existiert, so können wir $(f')'(x)$ auch als bilineare Abbildung $E\times E\to F$ auffassen (siehe (17.2.2)), und welche wir mit $f''(x)\in L(E,E;F)$ bezeichnen. Falls $f':E\supseteq U\to L(E,F)$ auf ganz $U$ differenzierbar ist, so nennen wir $f$ zweimal differenzierbar. Die Ableitung $(f')'$ von $f'$ ist dann eine Abbildung $(f')':E\supseteq U\to L(E,L(E,F))$ und vermöge der Identification von $L(E_1,L(E_2,F))$ mit $L(E_1,E_2;F)$ aus (17.2.2) erhalten wir eine Abbildung $f'':E\supseteq U\to L(E,E;F)$ die sogenannte zweite Ableitung von $f$ gegeben durch

$$f''(x)(v,w):=(f')'(x)(v)(w).$$

Rekursiv nennen wir $f$ $n+1$-mal (stetig) differenzierbar, falls $f'$ $n$-mal (stetig) differenzierbar ist. Wir schreiben dafür $f\in D^{n+1}$ ( $f\in C^{n+1}$). Schließlich heißt $f$ glatt (kurz $f\in C^{\infty}$), wenn $f$ beliebig oft differenzierbar ist.

Unter der $(n+1)$-ten Ableitung einer $(n+1)$-mal differenzierbaren Funktion $f:E\supseteq U\to F$ versteht man

$$f^{(n+1)}:E\supseteq U\overset{(f')^{(n)}}{\to} L_n(E,\dots,E;L(E,F)) \cong L_{n+1}(E,\dots,E;F).$$

Beachte die Schreibweise $f^{(n)}$ für höhere Ableitungen, denn $f',f'',f''',\dots$ läßt sich schlecht allgemein aufschreiben, darum setzen wir $f^{(0)}:=f$, $f^{(1)}:=f'$, $f^{(2)}:=f''$,....

Wegen $f'(x)(v)=d_vf(x)$ können wir $f^{(n)}(x)(v_1,\dots,v_n)$ wie folgt durch iterierte Richtungsableitungen berechnen:

$$f^{(n)}(x)(v_1,\dots,v_n) = d_{v_1}(d_{v_2}(\dots(d_{v_n} f)\dots))(x) = d_{v_1} d_{v_2} \dots d_{v_n} f (x).$$

Wir benötigen zuerst den folgenden Spezialfall der Kettenregel für höhere Differenzierbarkeit.

19.1.2 Lemma. Kettenregel für lineare äußere Funktion.
Es sei $a$ linear und $f\in D^p$. Dann ist $a\o f\in D^p$.

Beweis. Für $p=1$ wissen wir, daß $(a\o f)'=a_*\o f$ und da $a_*:L(E,F_1)\to L(E,F_2)$ linear ist, können wir Induktion anwenden.     []

Folglich ist die Differenzierbarkeitsklasse zweier Abbildungen gleich, falls diese auf einem linearen Isomorphismus der Bildräume gleich sind, Wir wollen die Bezeichnung $f\simeq g$ benützen, wenn $f=\alpha \o g$ ist für irgendeinen natürlichen linearen Isomorphismus zwischen den Bild-Räumen.

19.1.3 Lemma. Kettenregel für höhere Differenzierbarkeit.

(1)

Jede multilineare Abbildung ist glatt.

(2)

Die Kettenregel ist gültig für $C^p$ und $D^p$ für $p\in\{1,2,\dots,{\infty}\}$.

Beweis. Induktion bezüglich der Differentiationsordnung $p$:
( $p=0$) ist trivial.
( $p=1$) haben wir bereits früher in (17.2.1) & (17.3.3) gezeigt.
( $p+1$) (1) Für $(p=1)$ wissen wir, daß

$$T'(x_1,\dots,x_n)(v_1,\dots,v_n) =\sum_i \d _i T(x_1,\dots,x_n)(v_i)$$

$$= T(v_1,x_2,\dots,x_n)+\dots+ T(x_1,\dots,x_{n-1},v_n)$$

und der $j$-te Summand durch gegeben ist

$$\xymatrix{ E_1\times \dots\times E_n\ar[-0,1] ... ...n\ar[-0,1]_{T\check{}} &L(E_i,F) \ar[-1,0]_{\operatorname{pr}_i^*} \\ }$$

Der untere Pfeil ist $n-1$-linear und die vertikalen Pfeilen sind lineare, daher sind alle nach Induktions-Voraussetzung $D^p$. Also ist auch $T'$ $D^p$ (da Summieren linear ist) und daher ist $T$ $D^{p+1}$.
(2) Für $(p=1)$ haben wir, daß

$$(f\o g)' = \operatorname{komp}\o (f'\o g,g').$$

Wenn $f$ und $g$ beide $D^{p+1}$ sind, erhalten wir, daß $f'$ und $g'$ $D^p$ sind und $g$ $D^p$ ist(!). Also ist $(f'\o g,g')$ $D^p$ da (!) nach der Kettenregel für $p$ die Komponenten $D^p$ sind. Da $\operatorname{komp}$ bilinear ist, folgt das Resultat von (1) und der Kettenregel für $p$.

Für $C^p$ erhalten wir die Resultate durch Induktion, denn wenn $f$ $D^{p+1}$ ist, so ist $f$ $C^p$.     []

Beachte, daß wir für affine und bilineare Abbildungen (1) direkt zeigen könnten ohne die Kettenregel zu benützen, denn die Ableitung einer bilineare Abbildung ist linear und, die einer linearen Abbildung ist konstant. Jedoch ist die Ableitung eine 3-linearen Abbildung nicht bilinear!

19.1.4 Lemma. Differenzierbarkeit in Schritten.
Es sei $0\leq p<{\infty}$ und $0\leq q\leq{\infty}$ und $f:E\supseteq U\to F$. Dann gilt:

$$f D^{p+q} \Leftrightarrow f D^p f^{(p)} D^q.$$

$$f C^{p+q} \Leftrightarrow f C^p f^{(p)} C^q.$$

Beweis. Wir zeigen dies durch Induktion nach $p$. Für $p=0$ ist nichts zu zeigen.
$(p+1)$ $(\Rightarrow)$

$$f\in D^{p+q+1}$$

$$\Rightarrow f\in D,\; g:=f'\in D^{p+q}$$

$$\Rightarrow f\in D,\; f'=g\in D^p,\; g^{(p)}\in D^q$$

$$\Rightarrow f\in D^{p+1},\; f^{(p+1)}\simeq (f')^{(p)}\in D^q .$$

( $\Leftarrow)$

$$f\in D^{p+1},\; (f')^{(p)}\simeq f^{(p+1)}\in D^q$$

$$\Rightarrow f\in D,\; g:=f'\in D^p,\; g^{(p)}\in D^q$$

$$\Rightarrow f\in D,\; f'=g\in D^{p+q}$$

$$\Rightarrow f\in D^{1+p+q} .$$

Für stetige Differenzierbarkeit haben wir nur zu zeigen, daß $f\in C^{p+q}\Rightarrow f\in C^p$. O.B.d.A. sei $q>0$. Dann ist $f\in D^{p+1}$ wegen $(\Rightarrow)$ und daher $f\in D^p$ und $f^{(p)}\in D$. Somit ist $f^{(p)}\in C$, d.h. $f\in C^p$.     []

Wir wollen als nächstes (17.3.1) auf höhere Differenzierbarkeit verallgemeinern, d.h. aus der Existenz der iterierten partiellen Ableitungen $\d _{i_1}\dots \d _{i_p} f$ und einer geeigneten Stetigkeitsbedingung auf $f\in C^p$ schließen.

19.1.5 Proposition. Höhere Differenzierbarkeit via partielle Ableitungen.
Es ist $f:E=\mathbb{R}^n\supseteq U\to F$ genau dann $C^p$, wenn alle iterierten partiellen Ableitungen $\d _{i_1}\dots\d _{i_p}f:U\to F$ mit $i_1,\dots,i_p\in\{1,\dots,n\}$ existieren und stetig sind. Weiters haben wir dann

$$f^{(p)}(x)(v_1,\dots,v_p) = \sum_{i_1=1}^n\do... ..._{i_1}\cdots \d _{i_p} f(x) \cdot v_1^{i_1}\cdot\ldots\cdot v_p^{i_p},$$

wobei $v_i^j$ die $j$-te Koordinate von $v_i$ bezeichnet.

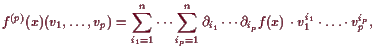
Beweis. Man zeigt dies mittels Induktion wie in (17.3.3), denn $f^{(p)}(x)$ ist $p$-linear und somit ist

$$f^{(p)}(x)(v_1,\dots,v_p) = f^{(p)}(x)\Bigl(\sum_{i_1}v_1^{i_1} e_{i_1},\dots,\sum_{i_p}v_p^{i_p} e_{i_p}\Bigr)$$

$$= \sum_{i_1}\dots\sum_{i_p} v_1^{i_1}\dots v_p^{i_p} \cdot f^{(p)}(x) ( e_{i_1},\dots,e_{i_p})$$

$$=\sum_{i_1,\dots,i_p} v_1^{i_1}\dots v_p^{i_p} \cdot \d _{i_1}\dots\d _{i_p} f(x).{\rm\quad[]}$$

19.1.6 Beispiel. Zweite Ableitung.
Es sei $f:\mathbb{R}^2\to\mathbb{R}$ gegeben durch $f(x,y)=x^2\cdot \sin(y)$. Dann ist

$$\d _1 f(x,y) \; =\; 2 x\phantom{{}^2}\cdot \sin(y)$$

$$\d _1\d _1 f(x,y) \; =\; 2 \phantom{x{}^2}\cdot \sin(y)$$

$$\d _2\d _1 f(x,y) \; =\; 2 x\phantom{{}^2}\cdot \cos(y)$$

$$\d _2 f(x,y) \; =\; \phantom{2} x^2 \cdot \cos(y)$$

$$\d _1\d _2 f(x,y) \; =\; 2 x\phantom{{}^2}\cdot \cos(y)$$

$$\d _2\d _2 f(x,y) \; =\; -x^2\cdot \sin(y)$$

Die Ableitung $f'(z)$ mit $z:=(x,y)$ wirkt also durch

$$f'(z)(u_1,u_2) = \Bigl(\d _1f(z), \d _2 f(z)\Bigr) \cdot \begin{pmatrix}u_1 u_2 \end{pmatrix}.$$

Für die zweite Ableitung $f''(z)$ erhalten wir

$$f''(z) (u_1,u_2;v_1,v_2) = (f')'(z)(u_1,u_2)(v_1,v_2) = (\d _1 f'(z) u_1 + \d _2 f'(z) u_2)(v_1,v_2)$$

$$= \d _1 \d _1 f(z) u_1 v_1 + \d _1\d _2 f(z) u_1 v_2 +\d _2 \d _1 f(z) u_2 v_1 + \d _2\d _2 f(z) u_2 v_2$$

$$= ( u_1 , u_2 ) \cdot \begin{pmatrix}\d _1\d _1 f(z) & \d _1\d _2... ...) & \d _2\d _2 f(z) \end{pmatrix} \cdot \begin{pmatrix}v_1 v_2 \end{pmatrix}$$

Wer sich wundert, daß man für die zweite Ableitung auch gemischte partielle Ableitungen wie $\d _1\d _2 f$ berücksichtigen muß, betrachte folgendes Beispiel:

$$f(x,y):=x\cdot y$$

Bei festem $x$ beschreibt $f$ eine Gerade $y\mapsto x y$ mit Anstieg $x$ und analog für $y$. Die iterierten Ableitungen $\d _1\d _1 f$ und $\d _2\d _2 f$ sind also überall 0. Wenn wir die Funktion $f$ nun mittels einer Rotation $R$ um $45^o$ drehen, also anstelle der standard Koordinatenrichtungen $e_1$ und $e_2$ die um $-45^o$ gedrehten Richtungen $b_i:=R^{-1}(e_i)$ verwenden und somit wegen

$$[R] =\begin{pmatrix}\cos(\frac{\pi}4) & -\sin(... ...d{pmatrix}=\frac1{\sqrt{2}}\begin{pmatrix}1 & -1 1 & 1 \end{pmatrix}$$

nach (10.25). Da nach (10.20a) für die Basiswechselabbildung $R:b_i\mapsto e_i$ die Gleichung $[R]_{B,B}=[R]_{E,E}=[\operatorname{id}]_{E,B}$ gilt, sind die neuen Koordinaten

$$\binom{u}{v}:=[R]\cdot\binom{x}{y}=\frac1{\sqrt{2}}\binom{x-y}{x+y}$$

in $\mathbb{R}^2$ betrachten, so ist $f$ in diesen neuen Koordinaten durch

$$\tilde f:=f\o R:(u,v)\mapsto (x,y)\mapsto f(x,... ...ot y=\tfrac1{\sqrt{2}}(u+v)\cdot \tfrac1{\sqrt{2}}(v-u)=\frac{v^2-u^2}2$$

gegeben, denn

$$\binom{x}{y}=[R^{-1}]\cdot\binom{u}{v}=\frac1{\sqrt{2}}\binom{u+v}{-u+v}.$$

Parallel zu den neuen Koordinatenachsen $b_1$ und $b_2$ wird $\tilde f$ nun durch Parabeln beschrieben und sowohl $\d _1\d _1\tilde f=-1$ als auch $\d _2\d _2\tilde f=1$ verschwinden nicht mehr. Mittels Kettenregel erhalten wir

$$(f\o R)'(u,v)\binom{h_1}{h_2} =f'(R(u,v)) \Bigl(R\binom{h_1}{h_2}\Bigr) =(f'\o R)(u,v) \Bigl(R\binom{h_1}{h_2}\Bigr)$$

und somit

$$(f\o R)''(u,v)\Bigl(\binom{h_1}{h_2},\binom{k_1}{k_2}\Bigr) =\Bigl((f\o R)'\Bigr)'(u,v)\binom{h_1}{h_2}\binom{k_1}{k_2}$$

$$=\Bigl(f'\o R\Bigr)'(u,v)\binom{h_1}{h_2}\Bigl(R\binom{k_1}{k_2}\Bigr)$$

$$=\Bigl((f')'\o R\Bigr)(u,v)\Bigl(R\binom{h_1}{h_2}\Bigr)\Bigl(R\binom{k_1}{k_2}\Bigr)$$

$$=\Bigl((f')'(R(u,v))\Bigr)\Bigl(R\binom{h_1}{h_2}\Bigr) \Bigl(R\binom{k_1}{k_2}\Bigr)$$

$$=\Bigl(f''(R(u,v))\Bigr)\Bigl(R\binom{h_1}{h_2},R\binom{k_1}{k_2}\Bigr)$$

Somit berechnet sich $\d _2\d _2\tilde f$ auch wie folgt

$$\d _2\d _2 (f\o R)(u,v) = (f \o R)''(u,v)(e_2,e_2) = f''(x,y) (R e_2,R e_2) = f''(x,y) (b_2,b_2)$$

$$=f''(x,y) \Bigl(\frac1{\sqrt{2}}\binom{1}{1},\frac1{\sqrt{2}}\binom{1}{1}\Bigr)$$

$$= \d _1\d _1 f(x,y) \frac1{\sqrt{2}} \frac1{\sqrt{2}} +\d _1\d _2 f(x,y) \frac1{\sqrt{2}} \frac1{\sqrt{2}}$$

$$\quad +\d _2\d _1 f(x,y) \frac1{\sqrt{2}} \frac1{\sqrt{2}} +\d _2\d _2 f(x,y) \frac1{\sqrt{2}} \frac1{\sqrt{2}}$$

$$=0+\frac12+\frac12+0=1$$

Man beachte, daß in diesen Beispielen $\d _1\d _2 f(z)=\d _2\d _1 f(z)$ gilt. Daß dies ziemlich allgemein der Fall ist, zeigt folgender Satz:

19.1.7 Satz von Schwarz.
Es sei $f:E\supseteq U\to F$ und $u,v\in E$ gegeben. Wir nehmen an, daß $d_u f(x)$, $d_vf(x)$ und $d_ud_v f(x)$ existieren und stetig in $x\in U$ sind. Dann existiert $d_vd_u f(x)$ und stimmt überein mit $d_ud_v f(x)$.

Beweis. Es ist

$$(d_ud_v f)(x) = \lim_{t\to 0+} \frac{d_vf(x+tu)-d_vf(x)}{t}$$

$$= \lim_{t\to 0+} \lim_{s\to 0+} \left(\frac{f(x+tu+sv)-f(x+tu)}s - \frac{f(x+sv)-f(x)}s\right) \cdot \frac1{t}$$

$$= \lim_{t\to 0+} \lim_{s\to 0+} \varphi (t,s),$$

wo

$$\varphi (t,s) := \left(\frac{f(x+tu+sv)-f(x+tu)}s - \frac{f(x+sv)-f(x)}s\right) \cdot \frac1{t}$$

$$= \Bigl(\int_0^1 d_v f(x+tu+\sigma sv) d\sigma - \int_0^1 d_v f(x+\sigma sv) d\sigma \Bigr)\cdot \frac1t$$

$$= \int_0^1 \frac{d_v f(x+tu+\sigma sv) - d_v f(x+\sigma sv)}{t} d\sigma$$

$$= \int_0^1 \int_0^1 d_u d_v f(x+\tau tu+\sigma sv) d\tau d\sigma \to$$

$$\qquad\to \int_0^1 \int_0^1 d_u d_v f(x+\tau tu) d\tau d\sigma ,$$

für $s\to 0+$ gleichmäßig in $t\in [-1,1]$, da wegen der Stetigkeit von $\d _1\d _2 f$

$$d_u d_v f(x+\tau tu+\sigma sv)\to d_u d_v f(x+\tau tu)$$    für $$s\to 0+$$ glm. in $$\tau ,t,\sigma .$$

Für $s\ne 0$ existiert wegen der Existenz von $d_u f$

$$\lim_{t\to 0+} \varphi (t,s) = \lim_{t\to 0+} \frac{f(x+tu+sv)-f(x+tu) - f(x+sv)+f(x)}{t s}$$

$$= \frac{d_u f(x+sv) - d_u f(x)}s$$

Damit ist $\varphi$ stetig bei 0 und wir erhalten

$$\exists d_vd_u f(x) := \lim_{s\to 0+} \lim_{t\to 0+} \varphi (t,s) = \lim_{s\to 0+, t\to 0+} \varphi (t,s)$$

$$= \lim_{t\to 0+} \lim_{s\to 0+} \varphi (t,s) = d_ud_v f(x){\rm\quad[]}$$

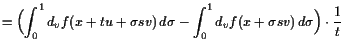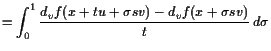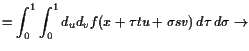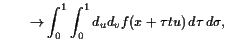Beispiel.
Betrachte

$$f(x,y) := \left\{\begin{array}{ll} 0 &\text{fü... ...}4 = r^2\frac{\sin(4\varphi )}4 &\text{andernfalls.} \end{array}\right.$$

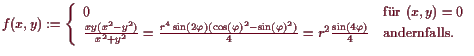
Dann existiert $\d _i\d _j$ für alle $i,j$, aber $\d _1\d _2 f(0,0)\ne \d _2\d _1 f(0,0)$.
In der Tat $\d _1f(0,y)=-y$, $\d _2f(x,0)=x$ und daher erhalten wir $\d _2\d _1 f(0,0)=-1\ne 1=\d _1\d _2 f(0,0)$.

Folgerung.
Es sei $f:E\supseteq U\to F$ $C^p$. Dann ist $f^{(p)}(x)$ symmetrisch für alle $x\in U$.

Beweis. Wir zeigen dies mittels Induktion nach $p$. Für $(p=2)$ ist das (19.1.7), denn $f''(x)(u,v)=\d _1\d _2 g(0,0)$ gilt, wobei $g(t,s):=f(x+t u+s v)$.

Für $(p+1)$ haben wir

$$f^{(p+1)}(x)(v_1,\dots,v_{p+1}) := (f')^{(p)}(x)(v_1,\dots,v_p)(v_{p+1}).$$

Da $g:=f':U\to L(E,F)$ $C^p$ ist, erhalten wir nach Induktions-Hypothese, daß der Ausdruck $g^{(p)}(x)(v_1,\dots,v_p)$ symmetrisch in $(v_1,\dots,v_p)$ ist und

$$g^{(p)}(x)(v_1,\dots,v_p) = (g')^{(p-1)}(x)(v_1,\dots,v_{p-1})(v_p).$$

Also ist

$$f^{(p+1)}(x)(v_1,\dots,v_{p+1}) = g^{(p)}(x)(v_1,\dots,v_p)(v_{p+1})$$

symmetrisch in $(v_1,\dots,v_p)$ und

$$f^{(p+1)}(x)(v_1,\dots,v_{p+1}) = (g')^{(p-1)}(x)(v_1,\dots,v_{p-1})(v_p)(v_{p+1})$$

$$= ((f')')^{(p-1)}(x)(v_1,\dots,v_{p-1})(v_p)(v_{p+1})$$

$$= (f'')^{(p-1)}(x)(v_1,\dots,v_{p-1})(v_p,v_{p+1})$$

ist symmetrisch in $(v_p,v_{p+1})$ da $f''(x)$ symmetrisch ist. Somit folgt das Resultat, da die Permutationen von $\{1,\dots,p+1\}$ erzeugt werden durch jene von $\{1,\dots,p\}$ und die Transposition $(p,p+1)$.     []

Bemerkung.
Es sei $f:E\supseteq U\to F$ $p$-mal differenzierbar. Dann ist nach (19.1.5)

$$f^{(p)}(x)(v_1,\dots,v_p) = d_{v_1}\dots d_{v... ...dots,i_p} v_1^{i_1}\dots v_p^{i_p} \cdot \d _{i_1}\dots\d _{i_p} f(x).$$

Wenn wir nun die Symmetrie der $p$-ten Ableitung verwenden, so können wir die partiellen Ableitungen nach Größe des Index sortieren und brauchen nur den Koeffizienten von $(\d _1)^{p_1}\dots (\d _n)^{p_n}$ bestimmen, wobei $p_1+\dots+p_n=p$ und alle $p_i\geq 0$. Dieser ist gerade

$$\sum_{i_1,\dots,i_p} v_1^{i_1}\dots v_p^{i_p},$$

wobei die Summe über all jene Indizes $i_1,\dots,i_p$ läuft, von denen gerade $p_1$ viele $1$ sind, $p_2$ viele $2$ sind, ..., und $p_n$ viele $n$ sind. Ist insbesonders $v_1=\dots=v_n=v$, so ist der entsprechende Koeffizient $v_1^{i_1}\dots v_n^{i_n}=(v^1)^{p_1}\dots (v^n)^{p_n}$ und es gibt genau $\frac{p!}{p_1!\dots p_n!}$ viele solche Summanden (Anzahl der Möglichkeiten die $p=p_1+\dots+p_n$ vielen partiellen Ableitungen auf die Kästchen mit gegebener Koordinatenrichtung zu verteilen), d.h.

$$f^{(p)}(x)(v,\dots,v) = \sum_{p_1+\dots+p_n=p... ...(v^1)^{p_1}\dots (v^n)^{p_n} (\d _1)^{p_1}\dots (\d _n)^{p_n} f(x).$$