15.3 Grenzwerte

Um von sukzessiv besseren Approximationen $x_0$, $x_1$, $x_2$,... sprechen zu können benötigen wir folgenden Begriff:

15.3.1 Definition. Folge.
Unter einer (unendlichen) Folge in $X$ versteht man eine Abbildung $x:\mathbb{N}\to X$. Anstelle von $x(n)$ schreibt man auch $x_n$. Und statt der Folge $x$ spricht man auch von $(x_0,x_1,x_2,\dots)$ oder präziser $(x_n)_{n\in\mathbb{N}}$ oder noch kürzer $(x_n)_n$ oder ganz gewagt $(x_n)$.

Um nun eine exakte Formulierung dafür zu haben, daß sukzessive Approximationen $x_0$, $x_1$, $x_2$,...einen Punkt $x_{\infty}$ beliebig gut approximieren, geben wir folgende

15.3.2 Definition. Konvergenz.
Man sagt, daß eine Folge $x$ gegen ein $x_{\infty}\in X$ konvergiert (symbolisch: $x_n\to x_{\infty}$ für $n\to{\infty}$), wenn

$$\forall \varepsilon >0\exists N\in\mathbb{N}\forall n\geq N:d(x_n,x_{\infty})<\varepsilon ,$$

d.h. fast alle (i.e. alle bis auf endlich viele) Folgeglieder im offenen $\varepsilon$-Ball um $x_{\infty}$ liegen. Falls ein $x_{\infty}$ existiert, gegen welches die Folge $x$ konvergiert, so heißt $x$ konvergent, andernfalls divergent. Beachte, daß es zu einer gegebenen Folge $x$ nur ein $x_{\infty}$ geben kann  - der sogenannte Grenzwert oder Limes $\lim_{n\to{\infty}}x_n$ - gegen welches $x$ konvergiert, denn die Bälle um zwei Punkte $x_{\infty}\ne x_{\infty}'$ mit Radius kleiner als $d(x_{\infty},x_{\infty}')/2$ sind disjunkt. Beachte weiters, daß wir den offenen Ball äquivalent auch durch den abgeschlossenen Ball ersetzen können, denn $B_s(x_{\infty})\subseteq U_r(x_{\infty})\subseteq B_r(x_{\infty})$ für $s<r$.

15.3.3 Beispiel.
Nach dem Satz (6.6) von Eudoxos ist $\lim_{n\to{\infty}}\frac1n=0$.

Konvergenz von Folgen $x_n$ in metrischen Räumen wird wegen $x_n\to x_{\infty}$ $\Leftrightarrow$ $d(x_n,x_{\infty})\to 0$ auf die Konvergenz reellen Zahlenfolgen zurückgeführt. Das folgende Lemma zeigt dies auch auf andere Weise.

15.3.4 Lemma. (Koordinatenweise) Konvergenz in $\mathbb{R}^p$.
Es sei $x_n:=(x_n^1,\dots,x_n^p)\in\mathbb{R}^p$. Dann konvergiert $x_n\to x_{\infty}$ genau dann, wenn für jedes $i$ die $i$-te Koordinate $x_n^i\to x_{\infty}^i$ für $n\to{\infty}$ konvergiert .

Beweis. ( $\Rightarrow$) offensichtlich, wegen $\vert a^i-b^i\vert\leq \vert a-b\vert$.

( $\Leftarrow$) folgt aus

$$\vert a-b\vert = \sqrt{\sum_k \vert a^k-b^k\vert^2} \leq \sqrt{p} \max\{\vert a^k-b^k\vert:1\leq k\leq p\}{\rm\quad[]}$$

15.3.6 Proposition. Rechenregeln für Limiten reeller Zahlen.
Es konvergiere $x_n\to x_{\infty}$ und $y_n\to y_{\infty}$. Dann gilt

$\bullet$

$x_n\pm y_n\to x_{\infty}\pm y_{\infty}$.

$\bullet$

$x_n\cdot y_n\to x_{\infty}\cdot y_{\infty}$.

$\bullet$

$\frac{x_n}{y_n}\to \frac{x_{\infty}}{y_{\infty}}$, falls $y_{\infty}\ne 0$ ist.

Man kann diese Aussagen auch in Form von Gleichungen wie

$$\lim_{n\to{\infty}} (x_n\pm y_n)=\lim_{n\to{\infty}} x_n\pm\lim_{n\to{\infty}} y_n$$

formulieren. Beachte jedoch, daß dabei die Existenz der rechten Seite nötiger Weise vorausgesetzt wird, wie das Beispiel $\lim_{n\to{\infty}} (n-n)$ zeigt.

Beweis. Z.B. ist

$$\vert x_n\cdot y_n-x_{\infty}\cdot y_{\infty}\vert \leq \vert x_n\cdot y_n-x_{\infty}\cdot y_n\vert+\vert x_{\infty}\cdot y_n-x_{\infty}\cdot y_{\infty}\vert$$

$$\leq \undersetbrace{\leq K/\varepsilon }\to{\vert x_n-x_{\infty}\... ...ace{\leq\vert x_{\infty}\vert/\varepsilon }\to{\vert y_n-y_{\infty}\vert}\to 0,$$

da $y$ beschränkt ist (siehe (15.3.2)) und $x_n\to x_{\infty}$ sowie $y_n\to y_{\infty}$.

Ebenso ist

$$\left\vert\frac{1}{y_n}-\frac{1}{y_{\infty}}\right\vert \leq \frac{\vert y_{\infty}-y_n\vert}{\vert y_n\cdot y_{\infty}\vert}\to 0,$$

da $y_n\to y_{\infty}$ und somit $\vert y_n\cdot y_{\infty}\vert\to \vert y_{\infty}\vert^2\ne 0$, und somit $\frac1{\vert y_n\cdot y_{\infty}\vert}\leq \frac2{\vert y_{\infty}\vert^2}$ für fast alle $n$ ist.     []

Wir können das vorige Resultat auch wie folgt formulieren:

15.3.7 Folgerung. Raum der konvergenten Folgen.
Es ist der Raum $c:=\{x:\mathbb{N}\to\mathbb{R}:x$ ist konvergent$\}$ ein Vektorraum, ja sogar ein kommutativer Ring bezüglich der komponentenweisen Multiplikation. Die Abbildung $x\mapsto\lim x$ ist ein Ring-Homomorphismus von $c\to\mathbb{R}$.

Beweis. Daß $c$ ein Vektorraum und Ring ist und die Funktion $\lim:c\to\mathbb{R}$ linear und multiplikativ ist, folgt sofort aus den Rechenregeln für konvergente Folgen.     []

15.3.8 Beispiel.
Aus den Rechenregeln (15.3.6) und dem Satz (15.3.3) folgt $\lim_{n\to{\infty}}1/n^k=0$ für jedes $1\leq k\in\mathbb{N}$.

15.3.9 Lemma. Limiten rationaler Funktionen.
Es sei $f(n):=\frac{p(n)}{q(n)}$ eine rationale Funktion, d.h. $p$ und $q$ Polynome mit $q\ne 0$. Dann läßt sich $\lim_{n\to{\infty}}f(n)$ wie folgt berechnen. Man kürzt Zähler und Nenner durch die höchste auftretende Potenz $n^K$ von $n$ und erhält

$$\lim_n f(n) =\lim_n \frac{\frac{p_0}{n^K}+\dots+\frac{p_K}{1}}{\frac{q_0}{n^K}+\dots+\frac{q_K}{1}} =\frac{p_K}{q_K},$$

wobei dies nur dann existiert, wenn $\operatorname{grad}(p)\leq \operatorname{grad}(q)=:K$ ist. Andernfalls siehe (15.3.18).

15.3.10 Proposition. Monotone Konvergenz.
Jede konvergente Folge ist beschränkt.

Umgekehrt ist jede beschränkte monoton wachsende Folge $x=(x_n)_{n\in\mathbb{N}}$ reeller Zahlen konvergent und es gilt

$$\sup\{x_n:n\in\mathbb{N}\}=\lim_{n\to{\infty}}x_n.$$

Klarerweise heißt eine Folge $x$ in $\mathbb{R}$ monoton wachsend, wenn sie es als Abbildung $x:\mathbb{N}\to\mathbb{R}$ ist, d.h. $x_k<x_{k'}$ aus $k<k'$ folgt.

Beweis. Jede konvergente Folge ist beschränkt, denn es gibt ein $N\in\mathbb{N}$ mit $\vert x_n-x_{\infty}\vert<1$ für alle $n>N$ und somit liegt $x$ im Ball um $x_{\infty}$ mit Radius $\max\{1,\vert x_0-x_{\infty}\vert,\dots,\vert x_N-x_{\infty}\vert\}$.

Umgekehrt sei $x$ beschränkt. Dann existiert nach (6.5) $x_{\infty}:=\sup\{x_n:n\in\mathbb{N}\}$. Es ist $\lim_{n\to{\infty}} x_n=x_{\infty}$, denn sei $\varepsilon >0$, dann ist $x_{\infty}-\varepsilon$ keine obere Schranke und somit existiert ein $N\in\mathbb{N}$ mit $x_N>x_{\infty}-\varepsilon$ und damit $x_{\infty}-\varepsilon <x_N\leq x_n\leq x_{\infty}<\times _{\infty}+\varepsilon$ für alle $n\geq N$.     []

15.3.11 Beispiel. Limes von $1/n^a$.
Es sei $0<a:=\frac{p}{q}\in\mathbb{Q}$. Dann ist $\lim_n \frac1{n^a}=0$.
Offensichtlich ist $n\mapsto \frac1{n^a}$ fallend, denn $n\mapsto n^p$ ist wachsend und somit auch die Umkehrfunktion $n\mapsto n^{1/q}$ von $m\mapsto m^q$ und schlußendlich die Zusammensetzung $n\mapsto n^{p/q}=n^a$. Schließlich ist $m\mapsto 1/m$ fallend und damit auch $n\mapsto \frac1{n^a}$. Da $\frac1{n^a}>0$ ist, existiert nach (15.3.10) der Limes $\alpha :=\lim_n \frac1{n^a}\geq 0$. Somit ist nach (15.3.8) und (15.3.6) $0=\lim\frac1{n^p}=\lim(\frac1{n^{p/q}})^q=(\lim\frac1{n^a})^q=\alpha ^q$, d.h $\alpha =0$.

15.3.12 Beispiel. Limes der harmonischen Reihe.
Wir betrachten die Folge $s_n:=\sum_{k=1}^n \frac1k$ für $n\geq 1$ der Partialsummen der harmonischen Reihe. Diese heißt harmonisch, da $\frac1k$ gerade das harmonische Mittel $2/(1/a+1/b)$ der beiden benachbarten Terme $a:=\frac1{k-1}$ und $b:=\frac1{k+1}$ ist. Diese Folge ist offensichtlich (streng) monoton wachsend. Sie ist aber unbeschränkt also nicht konvergent, denn für $n=2^m$ erhalten wir

$$s_n = \sum_{k=1}^{2^m}\frac1{k} = 1+\sum_{j=1}... ...rac1k \geq \sum_{j=1}^m (2^{j}-2^{j-1})\frac1{2^j}=\frac{m}2\to{\infty}$$

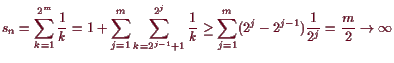
15.3.13 Beispiel. Limes von $q^n$.
Es sei $q\in\mathbb{R}$ und $x_n:=q^n$ die geometrische Folge. Der Name kommt daher, daß $x_n$ das (sogenannte) geometrische Mittel $\sqrt{x_{n-1} x_{n+1}}$ der benachbarten Folgeglieder ist.

Falls $q=0$ oder $q=1$ ist, so ist $x_n=q$ für $n\geq 1$ und somit $\lim_n x_n=q$. Ist $q=-1$, so ist $x_n=1$ für gerades $n$ und $x_n=-1$ für ungerades $n$ also sind $\pm 1$ zwei Kandidaten für den Grenzwert und $x_n$ ist nicht konvergent. Ist $q>1$, so ist $q^n=(1+(q-1))^n\geq 1+n (q-1)$ nach der Bernoulli-Ungleichung (siehe Proseminar Aufgabe 28) und somit unbeschränkt. Ist $q<-1$, so ist $\vert q^n\vert=\vert q\vert^n$ unbeschränkt und damit auch $q^n$. Ist $\vert q\vert<1$, so ist $\vert q^n\vert=(\frac1{1/\vert q\vert})^n$ und somit konvergent gegen 0, da nach dem zuvorgesagten $(\frac1{\vert q\vert})^n$ unbeschränkt ist und monoton ist.

15.3.14 Beispiel. Limes von $\root{n}\of{a}$.
Es sei $x_n:=\root{n}\of{a}$ mit $a\geq 0$. Falls $a\in\{0,1\}$, so ist $x_n=a$ und somit gegen $a$ konvergent. Ist $a>1$, so ist $x_n=:1+y_n$ mit $y_n>0$ und $a=x_n^n=(1+y_n)^n\geq 1+n y_n>n y_n$ nach der Bernoulli'schen Ungleichung. Also ist $0<y_n<\frac{a}{n}$ und somit $\lim_n y_n=0$ und damit $\lim_nx_n=1$.

Ist $0<a<1$ so ist nach dem vorigen $\lim_n \root{n}\of{1/a}=1$ und somit auch

$$\lim_n \root{n}\of{a}=\lim_n\frac1{\root{n}\of{1/a}}=1.$$

15.3.15 Beispiel. Limes von $\root{n}\of{n}$.
Es sei $x_n=\root{n}\of{n}$. Wieder setzen wir $x_n:=1+y_n$ mit $y_n>0$. Dann ist $n=(1+y_n)^n=1+ny_n+\binom{n}{2}y_n^2+\dots\geq \frac{n(n-1)}2 y_n^2$, also $0<y_n\leq\sqrt{2/(n-1)}$, also $\lim_n y_n=0$ und damit $\lim_nx_n=1$.

15.3.17 Definition. Uneigentliche Konvergenz.
Wir wollen nun die Definition von Konvergenz auf $\lim_n x_n=\pm{\infty}$ erweitern. Dazu bilden wir $\mathbb{R}$ mittels Zentralprojektion auf den bei 0 berührenden Einheitshalbkreis und dann weiter mittels Normalprojektion in das Intervall von -1 bis 1 ab. Explizit ist dieses streng monoton wachsende Abbildung durch $f:x\mapsto \frac{x}{\sqrt{1+x^2}}$ gegeben mit Umkehrabbildung $g:y\mapsto \frac{y}{\sqrt{1-y^2}}$. Es ist nun sinnvoll $f(\pm\infty):=\pm 1$ zu setzen.

Als neue Metrik $d$ für Punkte $x,y\in\mathbb{R}\cup\{\pm\infty\}$ definieren wir

$$d(x,y):=\vert f(x)-f(y)\vert.$$

Dann konvergiert eine Folge $(x_n)$ bezüglich $d$ genau dann gegen $x_{\infty}\in\mathbb{R}$, wenn sie es bezüglich der euklidischen Metrik tut. In der Tat, für $x\geq y$ ist

$$d(x,y)=\frac{x}{\sqrt{1+x^2}}-\frac{y}{\sqrt{1+y^2}}\leq \frac{x-y}{\sqrt{1+y^2}}\leq \vert x-y\vert$$

und umgekehrt ist $\vert x-y\vert<\varepsilon$ für $d(x,y)=\vert f(x)-f(y)\vert<\varepsilon /(1+(\vert y\vert+\varepsilon )^2)^{3/2}=\varepsilon f'(\vert y\vert+\varepsilon )$. Ist schließlich $y=+{\infty}$, so gilt $d(x,y)=\vert f(x)-1\vert<\varepsilon$ genau dann, wenn $f(x)>1-\varepsilon$ also $x=f(g(x))>g(1-\varepsilon )=\frac{1-\varepsilon }{\sqrt{1-(1-\varepsilon )^2}}=:K$ ist.

Somit haben wir $\lim_n x_n=\pm{\infty}$ einen Sinn geben der auch im Einklang zu unseren Definitionen von $\sup M=\pm{\infty}$ und $\inf M=\pm{\infty}$ steht.

15.3.18 Proposition. Rechenregel für uneigentliche Limiten.
Die Rechenregeln (15.3.6) gelten auch für uneigentliche Limiten, wenn man mit den Grenzwerten $\mathbb{R}\cup\{\pm\infty\}$ wie folgt rechnet.

$\bullet$

$p+(+\infty)=+\infty$ für $-\infty<p\leq+\infty$,

$\bullet$

$p+(-\infty)=-\infty$ für $-\infty\leq p<+\infty$,

$\bullet$

$(+\infty)+(-\infty)$ ist undefiniert,

$\bullet$

$p\cdot(\pm\infty)=\pm\infty$ für $0<p\leq+\infty$,

$\bullet$

$p\cdot(\pm\infty)=\mp\infty$ für $0>p\geq-\infty$,

$\bullet$

$0\cdot(\pm\infty)$ ist undefiniert,

$\bullet$

$p/(\pm\infty)=0$ für $-\infty<p<+\infty$,

$\bullet$

$\pm\infty/p=\pm\infty$ für $0<p<+\infty$,

$\bullet$

$\pm\infty/p=\mp\infty$ für $0>p>-\infty$,

$\bullet$

$(\pm\infty)/(\pm\infty)=0$ ist undefiniert.

Uneigentliche Grenzwerte rationaler Funktionen.
Es sei $f(n):=\frac{p(n)}{q(n)}$ eine rationale Funktion, d.h. $p$ und $q$ Polynome mit $q\ne 0$ und $K:=\operatorname{grad}(p)>\operatorname{grad}(q)=:L$. Dann ist

$$\lim_n f(n) =\lim_n n^{K-L}\cdot \frac{\frac{p... ...n^L}+\dots+\frac{q_L}{1}} =+{\infty}\cdot \frac{p_K}{q_L}=\pm {\infty},$$

je nachdem ob $p_K/q_L>0$ oder $p_K/q_L<0$ ist.