Nächste Seite: 11 Gleichungssysteme Aufwärts: Mathematik 1 für Informatik Vorherige Seite: 9 Erzeugenden-Systeme Inhalt Index
Um nun lineare Vektorräume mit einander in Beziehung setzen zu können, benötigen derartige Abbildungen zwischen diesen, die uns erlauben die Rechnungen die wir für die Vektoren eines Vektorraums durchgeführt haben entsprechend auf die Bilder dieser Vektoren in einen anderen Vektorraum zu übertragen.
10.1 Definition.
Unter einer linearen Abbildung (man sagt auch Homomorphismus oder
kurz Morphismus dafür) zwischen Vektorräumen
![]() und
und
![]() versteht man eine
Abbildung
versteht man eine
Abbildung
![]() die folgendes erfüllt
die folgendes erfüllt
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1013}\egroup](img2853.png)
![\bgroup\color{demo}\includegraphics[scale=0.5]{pic-1014}\egroup](img2854.png)
Es ist also egal ob man zuerst addiert bzw. skalarmultipliziert und dann die
Abbildung
![]() anwendet oder umgekehrt vorgeht.
anwendet oder umgekehrt vorgeht.
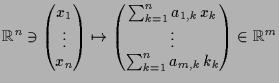 |
Beweis. Es ist
10.3 Definition.
Wie bei allgemeinen Abbildungen spielt natürlich auch bei linearen Abbildungen
die Injektivität,
die Surjektivität und vor allem die Bijektivität ein große Rolle. Man nennt eine
Abbildung
![]() zwischen Vektorräumen
zwischen Vektorräumen
10.4 Lemma.
Es sei
![]() linear. Dann ist der Kern
linear. Dann ist der Kern
![]() von
von
![]() ein Teilvektorraum von
ein Teilvektorraum von
![]() .
.
Dies zeigt wegen (10.2) nochmals 8.7 und 8.9.
Beweis. Seien
10.5 Lemma.
Eine lineare Abbildung
![]() ist genau dann injektiv, wenn
ist genau dann injektiv, wenn
![]() ist.
ist.
Beweis. (
(
![]() ) Es sei
) Es sei
![]() und
und
![]() . Dann ist
. Dann ist
![]() und somit
und somit
![]() , also
, also
![]() . D.h.
. D.h.
![]() ist injektiv.
[]
ist injektiv.
[]
10.6 Lemma.
Es sei
![]() linear. Dann ist das Bild
linear. Dann ist das Bild
![]() von
von
![]() ein Teilvektorraum von
ein Teilvektorraum von
![]() .
.
Beweis. Es sei
Die folgende Proposition zeigt, daß es genügt eine lineare Abbildung
![]() an nur sehr wenigen Stellen
an nur sehr wenigen Stellen
![]() zu kennen, um sie an allen Vektoren
zu kennen, um sie an allen Vektoren
![]() berechnen zu können.
berechnen zu können.
10.7 Proposition.
Es sei
![]() eine Basis des Vektorraums
eine Basis des Vektorraums
![]() und
und
![]() eine Abbildung in
einen Vektorraum
eine Abbildung in
einen Vektorraum
![]() .
Dann existiert eine eindeutig bestimmte lineare Abbildung
.
Dann existiert eine eindeutig bestimmte lineare Abbildung
![]() mit den vorgegebenen Werten
mit den vorgegebenen Werten
![]() auf den Basis-Vektoren
auf den Basis-Vektoren
![]() , d.h. mit
, d.h. mit
![]() .
.
Beweis. Da
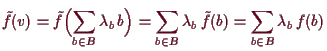
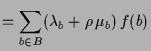 |
||
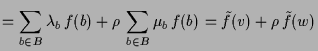 |
10.16 Proposition.
Es sei eine lineare Abbildung
![]() gegeben und
gegeben und
![]() die Bilder
die Bilder
![]() der Standard-Basis.
Dann
gilt:
der Standard-Basis.
Dann
gilt:
Beweis. Die Abbildung
Etwas allgemeiner gilt folgendes:
10.8 Proposition.
Es sei
![]() eine lineare Abbildung zwischen Vektorräumen.
eine lineare Abbildung zwischen Vektorräumen.
Beweis. (1) ist klar, da
(2) Es sei
![]() injektiv und
injektiv und
![]() linear unabhängig mit
linear unabhängig mit
![]() . Da
. Da
![]() injektiv ist existiert zu jedem
injektiv ist existiert zu jedem
![]() ein eindeutiges
ein eindeutiges
![]() mit
mit
![]() . Somit ist
. Somit ist
![]() .
Da
.
Da
![]() injektiv ist, ist also
injektiv ist, ist also
![]() und, da
und, da
![]() linear
unabhängig ist, ist
linear
unabhängig ist, ist
![]() für alle
für alle
![]() , also
, also
![]() für alle
für alle
![]() , d.h.
, d.h.
![]() ist linear unabhängig.
ist linear unabhängig.
Falls
![]() nicht injektiv ist, so existiert ein
nicht injektiv ist, so existiert ein
![]() mit
mit
![]() , also
ist
, also
ist
![]() linear unabhängig aber
linear unabhängig aber
![]() linear abhängig.
linear abhängig.
(3) Ist
![]() bijektiv und
bijektiv und
![]() eine Basis, dann ist
eine Basis, dann ist
![]() eine Basis
nach (1) und (2).
Umgekehrt sei das Bild jeder Basis eine Basis. Dann ist
eine Basis
nach (1) und (2).
Umgekehrt sei das Bild jeder Basis eine Basis. Dann ist
![]() surjektiv nach (1)
aber auch injektiv nach (2), denn sei
surjektiv nach (1)
aber auch injektiv nach (2), denn sei
![]() linear unabhängig.
Dann existiert nach (9.13.2) eine Basis
linear unabhängig.
Dann existiert nach (9.13.2) eine Basis
![]() . Somit ist nach
Voraussetzung auch
. Somit ist nach
Voraussetzung auch
![]() eine Basis, also linear unabhängig und ebenso die
Teilmenge
eine Basis, also linear unabhängig und ebenso die
Teilmenge
![]() .
[]
.
[]
Beachte, daß es in (2) und (3) nicht genügt für ein
![]() die Aussage zu haben.
Denn es ist
die Aussage zu haben.
Denn es ist
![]() ,
,
![]() nicht injektiv, dennoch
ist
nicht injektiv, dennoch
ist
![]() eine Basis in
eine Basis in
![]() und
und
![]() eine solche von
eine solche von
![]() .
.
10.9 Folgerung.
Es seien
![]() und
und
![]() Vektorräume. Dann gilt:
Vektorräume. Dann gilt:
Beweis. Sei
(1) Falls
![]() injektiv ist, so ist
injektiv ist, so ist
![]() linear unabhängig, also
linear unabhängig, also
![]() nach (9.13.4).
Umgekehrt sei
nach (9.13.4).
Umgekehrt sei
![]() eine Basis von
eine Basis von
![]() mit
mit
![]() , d.h. es existiert eine
injektive Abbildung
, d.h. es existiert eine
injektive Abbildung
![]() . Wir erweitern diese nach (10.7)
zu einer linearen Abbildung
. Wir erweitern diese nach (10.7)
zu einer linearen Abbildung
![]() . Diese ist injektiv, denn
aus
. Diese ist injektiv, denn
aus
![]() , wobei
, wobei
![]() und
und
![]() falls
falls
![]() ist. Da
ist. Da
![]() eine Basis ist
sind alle
eine Basis ist
sind alle
![]() und damit alle
und damit alle
![]() gleich 0.
gleich 0.
(2) Falls
![]() surjektiv ist, so ist
surjektiv ist, so ist
![]() ein Erzeugenden-System, also
ein Erzeugenden-System, also
![]() nach (9.13.5).
Umgekehrt sei
nach (9.13.5).
Umgekehrt sei
![]() eine Basis von
eine Basis von
![]() mit
mit
![]() , d.h. es existiert eine
surjektive Abbildung
, d.h. es existiert eine
surjektive Abbildung
![]() (eine Inverse zur injektiven
Abbildung
(eine Inverse zur injektiven
Abbildung
![]() ).
Wir erweitern diese nach (10.7)
zu einer linearen Abbildung
).
Wir erweitern diese nach (10.7)
zu einer linearen Abbildung
![]() . Diese ist surjektiv,
denn jeder Erzeuger
. Diese ist surjektiv,
denn jeder Erzeuger
![]() wird von
wird von
![]() und damit auch von
und damit auch von
![]() getroffen.
getroffen.
(3) folgt nun aus (1) und (2).
Falls
![]() und
und
![]() gleichmächtig sind, so existiert eine
bijektive Abbildung
gleichmächtig sind, so existiert eine
bijektive Abbildung
![]() und diese induziert wie in (1) und (2)
einen linearen Isomorphismus.
und diese induziert wie in (1) und (2)
einen linearen Isomorphismus.
Beachte, daß die Funktionen
![]() eine Basis bilden:
Erzeugenden-System ist klar und aus
eine Basis bilden:
Erzeugenden-System ist klar und aus
![]() folgt
folgt
![]() für alle
für alle
![]() .
[]
.
[]
10.15 Folgerung.
Isomorphe (endlich dimensionale) Vektorräume haben die selbe Dimension und umgekehrt.
Beweis.
![]() Nach (10.16) ist
Nach (10.16) ist
![]() .
[]
.
[]
10.10 Lemma.
Es sei
![]() ein linearer Teilraum eines Vektorraums
ein linearer Teilraum eines Vektorraums
![]() .
Wir betrachten die Äquivalenzrelation die durch
.
Wir betrachten die Äquivalenzrelation die durch
![]() gegeben ist.
Die von
gegeben ist.
Die von
![]() erzeugte Äquivalenzklasse ist
erzeugte Äquivalenzklasse ist
![]() .
Die Menge der Äquivalenzklassen wird mit
.
Die Menge der Äquivalenzklassen wird mit
![]() bezeichnet.
Schließlich sei
bezeichnet.
Schließlich sei
![]() die Abbildung
die Abbildung
![]() .
Dann existieren eindeutig bestimmte Operationen
.
Dann existieren eindeutig bestimmte Operationen
![]() und
und
![]() die
die
![]() zu einem Vektorraum
und
zu einem Vektorraum
und
![]() zu einer linearen Abbildung machen.
zu einer linearen Abbildung machen.
Beweis. Damit
10.11 Proposition.
Es sei
![]() ein linearer Teilraum eines Vektorraums. Dann gilt:
ein linearer Teilraum eines Vektorraums. Dann gilt:
Beweis. (1) Die Inklusion ist eine injektive lineare Abbildung
(2) Sei
![]() eine Basis von
eine Basis von
![]() , also linear unabhängig in
, also linear unabhängig in
![]() und wegen
und wegen
![]() auch eine Basis von
auch eine Basis von
![]() nach (9.13.2)
und damit
nach (9.13.2)
und damit
![]() .
.
(3) Sei
![]() eine Basis von
eine Basis von
![]() , also linear unabhängig in
, also linear unabhängig in
![]() und somit nach (9.13.2) zu einer Basis
und somit nach (9.13.2) zu einer Basis
![]() von
von
![]() erweiterbar.
Dann ist
erweiterbar.
Dann ist
![]() eine Basis von
eine Basis von
![]() , denn
da die kanonische Abbildung
, denn
da die kanonische Abbildung
![]() ,
,
![]() ,
surjektiv ist, ist
,
surjektiv ist, ist
![]() ein Erzeugenden-System
nach (10.8.1), also auch
ein Erzeugenden-System
nach (10.8.1), also auch
![]() eines.
Es ist
eines.
Es ist
![]() auch linear unabhängig, denn
aus
auch linear unabhängig, denn
aus
![]() folgt
folgt
![]() ,
also existieren
,
also existieren
![]() für alle
für alle
![]() mit
mit
![]() und
da
und
da
![]() linear unabhängig ist, sind alle
linear unabhängig ist, sind alle
![]() gleich 0.
Aso ist
gleich 0.
Aso ist
![]() ,
,
![]() und
und
![]() .
[]
.
[]
10.12 Proposition.
Es seien
![]() und
und
![]() zwei lineare Teilräume von
zwei lineare Teilräume von
![]() . Dann induziert
die Inklusion
. Dann induziert
die Inklusion
![]() einen Isomorphismus
einen Isomorphismus
![]() .
Insbesonders ist
.
Insbesonders ist
![]()
Beweis. Betrachte das Diagramm
![\bgroup\color{demo}$\displaystyle \xymatrix{
W'\ar@{->}[0,1] &W+W'\ar@{->}[0,1] ...
...[0,1] &W\ar@{->}[0,1] \ar@{->}[-1,0] &
W/(W\cap W')\ar@{.>}[-1,0] \\
} $\egroup](img2521.png)
10.13 Proposition.
Es seien
![]() und
und
![]() Teilräume von
Teilräume von
![]() .
Dann sind äquivalent:
.
Dann sind äquivalent:
Beweis. (1
(3
![]() 2)
Sei
2)
Sei
![]() . Wegen der Surjektivität von
. Wegen der Surjektivität von
![]() existiert ein
existiert ein
![]() mit
mit
![]() , also ist
, also ist
![]() und somit
und somit
![]() .
Angenommen
.
Angenommen
![]() ist eine zweite Darstellung. Dann ist
ist eine zweite Darstellung. Dann ist
![]() und somit
und somit
![]() wegen der Injektivität von
wegen der Injektivität von
![]() und damit auch
und damit auch
![]() .
.
(2
![]() 1)
Offensichtlich ist
1)
Offensichtlich ist
![]() wegen
wegen
![]() .
Sei
.
Sei
![]() , dann sind
, dann sind
![]() und
und
![]() zwei Darstellungen, also
zwei Darstellungen, also
![]() .
.
(1,3
![]() 4)
Aus
4)
Aus
![]() folgt
folgt
![]() und
und
![]() nach (1).
nach (1).
(4
![]() 3) Aus
3) Aus
![]() folgt die Injektivität
von
folgt die Injektivität
von
![]() . Wegen
. Wegen
![]() folgt auch
die Surjektivität.
[]
folgt auch
die Surjektivität.
[]
10.14 Proposition.
Es sei
![]() linear.
Dann induziert
linear.
Dann induziert
![]() einen Isomorphismus
einen Isomorphismus
![]() .
.
Folglich ist
![]() .
.
Beweis. Offensichtlich ist
Die Linearität von
![]() ergibt sich aus der Definition der Vektorraum-Operationen auf
ergibt sich aus der Definition der Vektorraum-Operationen auf
![]() .
.
Die Dimensionsformel ergibt sich vermöge (10.11.3) aus
![]() .
[]
.
[]
10.17 Definition.
Der Rang einer linearen Abbildung
![]() ist definiert als
ist definiert als
10.19 Matrizen versus linearer Abbildungen.
Die Abbildung
![]() gegeben durch
gegeben durch
![]() mit
mit
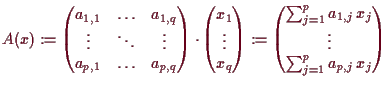
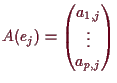
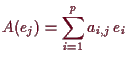
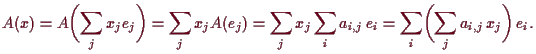
10.20 Matrixdarstellung linearer Abbildungen.
Es sei
![]() ein Vektorraum über
ein Vektorraum über
![]() mit endlicher Basis
mit endlicher Basis
![]() .
Dann ist die Abbildung
.
Dann ist die Abbildung
![]() ein Isomorphismus
ein Isomorphismus
![]() nach (10.16).
Seine Inverse bezeichnen wir mit
nach (10.16).
Seine Inverse bezeichnen wir mit
![]() .
.
Sei nun
![]() eine lineare Abbildung zwischen Vektorräumen über
eine lineare Abbildung zwischen Vektorräumen über
![]() und seien
und seien
![]() und
und
![]() Basen von
Basen von
![]() und
und
![]() .
Dann können wir statt
.
Dann können wir statt
![]() die lineare Abbildung
die lineare Abbildung
![]() betrachten:
betrachten:
![\bgroup\color{demo}$\displaystyle \xymatrix{
b_j\ar@{->}[0,3]_{f} \ar@{->}[3,0]^...
...m V'} & \\
e_j\ar@{.>}[0,3]^{\tilde f} & & &\sum_i f_{i,j}\,e_j' \\
} $\egroup](img2588.png)
10.18 Satz.
Die Menge
![]() der linearen Abbildungen zwischen Vektorräumen
der linearen Abbildungen zwischen Vektorräumen
![]() und
und
![]() über
über
![]() ist selbst ein Vektorraum.
ist selbst ein Vektorraum.
Ebenso ist die Menge
![]() der
der ![]() -Matrizen ein solcher.
-Matrizen ein solcher.
Für je eine Basis
![]() von
von
![]() und
und
![]() von
von
![]() haben wir einen Isomorphismus von Vektorräumen
haben wir einen Isomorphismus von Vektorräumen
Beweis. Falls
Dieser Isomorphismus zwischen linearen Abbildungen und Matrizen erlaubt uns zwischen diesen Konzepten hin- und herzuwechseln. Insbesonders können wir Begriffe (wie z.B. Injektivität, Surjektivität, Kern, Rang, etc. ) die wir für lineare Abbildungen eingeführt haben auch für Matrizen verwenden.
10.21 Folgerung.
Der Rang einer linearen Abbildung
![]() ist
maximale Anzahl linear unabhängiger Spaltenvektoren einer/jeder
Matrixdarstellung von
ist
maximale Anzahl linear unabhängiger Spaltenvektoren einer/jeder
Matrixdarstellung von
![]() .
.
Beweis. Es sei
10.22 Beispiel einer Matrixdarstellung.
Es sei
![]() und
und
![]() die Abbildung
die jeden Vektor
die Abbildung
die jeden Vektor
![]() in
in
![]() den normal-Vektor
den normal-Vektor
![]() (siehe (14.12)) zuordnet.
Als Basis
(siehe (14.12)) zuordnet.
Als Basis
![]() von
von
![]() verwenden wir z.B.
verwenden wir z.B.
![]() und
und
![]() .
Dann ist
.
Dann ist
![]() und
und
![]() und somit
und somit
![\bgroup\color{demo}$\displaystyle [A]_{B,B}=\begin{pmatrix}1 & -2 \\ 2 & -1 \end{pmatrix}.
$\egroup](img2627.png)
10.23 Matrizen-Multiplikation.
Die Komposition von linearen Abbildungen läßt sich in eine Multiplikation
der entsprechenden Matrizen übersetzen.
Dabei wird eine
![]() -Matrix
-Matrix
![]() mit einer
mit einer
![]() -Matrix
-Matrix
![]() zur
zur
![]() -Matrix
-Matrix
![]() mit
mit
![]() aufmultipliziert. Also erhält man den Koeffizienten von
aufmultipliziert. Also erhält man den Koeffizienten von
![]() in der
in der
![]() -ten
Zeile und
-ten
Zeile und
![]() -ten Spalte durch komponentenweise Multiplikation
der
-ten Spalte durch komponentenweise Multiplikation
der
![]() -ten Zeile der 1.ten Matrix mit der
-ten Zeile der 1.ten Matrix mit der
![]() -ten Spalte der 2.ten Matrix
und Aufsummieren dieser
-ten Spalte der 2.ten Matrix
und Aufsummieren dieser
![]() vielen Produkte.
vielen Produkte.
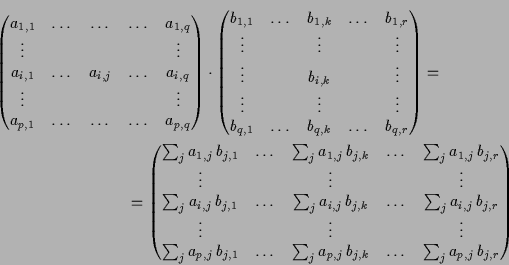
Beweis. Es sei
Bemerkung.
Die in (10.24) definierte Matrizenmultplikation
verallgemeinert die Wirkung von Matrizen
![]() auf
Vektoren
auf
Vektoren
![]() aus
(10.2.3). Denn sei
aus
(10.2.3). Denn sei
![]() die zugehörige lineare
Abbildung also
die zugehörige lineare
Abbildung also
![]() dann ist
dann ist
![]() .
Allgemeiner gilt somit für
.
Allgemeiner gilt somit für
![]() bzgl. Basen
bzgl. Basen
![]() von
von
![]() und
und
![]() von
von
![]() die Beziehung
die Beziehung
10.24 Proposition.
Es ist sowohl
![]() also auch
also auch
![]() ein Ring bezüglich
Addition und Komposition, der sogenannte Endomorphismenring.
Der lineare Isomorphismus
ein Ring bezüglich
Addition und Komposition, der sogenannte Endomorphismenring.
Der lineare Isomorphismus
![]() ist ein Ring-Homomorphismus, d.h. auch mit der Multiplikation verträglich.
ist ein Ring-Homomorphismus, d.h. auch mit der Multiplikation verträglich.
Beweis. Die Distributivität der Komposition bzgl. der 1. Variable gilt allgemein, jene bzgl. der 2. Variable hängt an der Linearität des 1. Arguments.
Die Ring-Homomorphie folgt aus (10.23). []
10.25 Beispiel.
Wir betrachten Drehungen
![]() in der Ebene
in der Ebene
![]() um den 0-Punkt und den Winkel
um den 0-Punkt und den Winkel
![]() .
Es ist
.
Es ist
![]() homogen, denn Geraden
homogen, denn Geraden
![]() werden auf Geraden abgebildet und Längen der Vektoren
werden unter Drehungen erhalten, also ist
werden auf Geraden abgebildet und Längen der Vektoren
werden unter Drehungen erhalten, also ist
![]() ,
d.h.
,
d.h.
![]() , und somit
, und somit
![]() , also
, also
![]() , da die Reihenfolge
von
0,
, da die Reihenfolge
von
0,
![]() und
und
![]() auf der von ihnen erzeugten Geraden unter
auf der von ihnen erzeugten Geraden unter
![]() erhalten bleibt.
Weiters ist
erhalten bleibt.
Weiters ist
![]() additiv, da Parallelogramme (mit den Ecken
0,
additiv, da Parallelogramme (mit den Ecken
0,
![]() ,
,
![]() ,
,
![]() ) auf ebensolche abgebildet werden, also
) auf ebensolche abgebildet werden, also
![]() .
.
![\includegraphics[scale=0.5]{pic-1047}](img2674.png)
![\includegraphics[scale=0.5]{pic-1046}](img2675.png)
Wir versuchen nun die Matrixdarstellung dieser linearen Abbildung zu bestimmen.
Das Bild des 1. Einheitsvektors
![]() ist
ist
![]() und jenes des 2. Einheitsvektors
und jenes des 2. Einheitsvektors
![]() ist
ist
![]() .
Die Matrix von
.
Die Matrix von
![]() ist folglich durch
ist folglich durch
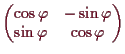
![\includegraphics[scale=0.7]{pic-1018}](img2681.png)
Beachte jedoch, daß die Matrixdarstellung
![]() bezüglich anderer Basen keine so schöne Form mehr haben muß:
Sei z.B.
bezüglich anderer Basen keine so schöne Form mehr haben muß:
Sei z.B.
![]() mit
mit
![]() und
und
![]() und somit
und somit
![]() Dann ist
Dann ist
![\bgroup\color{demo}$\displaystyle [f_\varphi ]_{B,B}=\Bigl([f(b_1)]_B,[f(b_2)]_B...
... -2\sin\varphi \\
\sin\varphi & \sin\varphi +\cos\varphi
\end{pmatrix}$\egroup](img2694.png)
10.26 Additionstheoreme.
Die Zusammensetzung zweier Drehungen
![]() und
und
![]() ist ebenfalls
eine Drehung und zwar jene um den Winkel
ist ebenfalls
eine Drehung und zwar jene um den Winkel
![]() , d.h.
, d.h.
![]() .
Die entsprechende Gleichung der zugehörigen Matrizen lautet wegen (10.23)
.
Die entsprechende Gleichung der zugehörigen Matrizen lautet wegen (10.23)
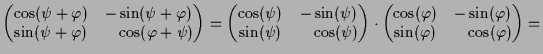 |
||
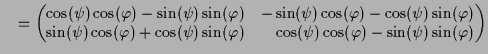 |
Ein Vergleich der Eintragungen liefert die Additionstheoreme für Sinus und Cosinus.
10.27 Beispiel.
Wir bestimmen nun alle invertierbaren
![]() -Matrizen
-Matrizen
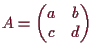
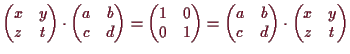
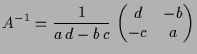 |
10.28 Beispiel.
Wir betrachten den Vektorraum
![]() der Polynome mit reellen Koeffizienten.
Die Polynome
der Polynome mit reellen Koeffizienten.
Die Polynome
![]() vom Grad
vom Grad
![]() bilden einen Teilraum
bilden einen Teilraum
![]() von
von
![]() .
.
Das Differenzieren
![]() ist gegeben durch
ist gegeben durch
![]() , d.h. die Basis-Vektoren
, d.h. die Basis-Vektoren
![]() werden auf
werden auf
![]() abgebildet, d.h.
abgebildet, d.h.
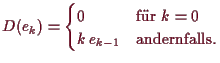

Ein weiteres Beispiel ist Multiplikation
![]() mit einem Polynom
mit einem Polynom
![]() .
Sei z.B.
.
Sei z.B.
![]() und
und
![]() .
Dann bildet
.
Dann bildet
![]() das Basispolynom
das Basispolynom
![]() auf
auf
![]() ab.
Die Matrixdarstellung von
ab.
Die Matrixdarstellung von
![]() ist somit
ist somit
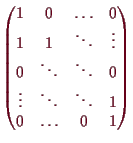
Wir betrachten das Verschieben
![]() um den Wert
um den Wert
![]() gegeben durch
gegeben durch
![]() .
Wie sieht nun eine Matrixdarstellung von
.
Wie sieht nun eine Matrixdarstellung von
![]() aus.
Die Bilder der standard-Basis sind
aus.
Die Bilder der standard-Basis sind
![]() , also
ist die Matrixdarstellung gegeben durch
, also
ist die Matrixdarstellung gegeben durch
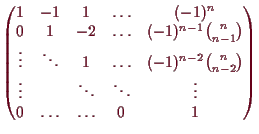
Ein anderes Beispiel ist die Zusammensetzung von rechts
![]() ,
,
![]() , also
, also
![]() , wobei
, wobei
![]() ist.
Es ist
ist.
Es ist
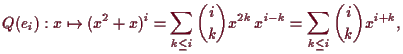

10.20a Basiswechsel.
Wir haben in (10.20) die Matrixdarstellung
![]() einer linearen Abbildung
einer linearen Abbildung
![]() bzgl. Basen
bzgl. Basen
![]() auf
auf
![]() und
und
![]() auf
auf
![]() als
als
![]() definiert.
Sei nun eine zweite Basis
definiert.
Sei nun eine zweite Basis
![]() von
von
![]() sowie und
sowie und
![]() von
von
![]() gegeben.
Der Zusammenhang zwischen
gegeben.
Der Zusammenhang zwischen
![]() und
und
![]() ist durch folgendes Diagramm gegeben:
ist durch folgendes Diagramm gegeben:
![\bgroup\color{demo}$\displaystyle \xymatrix{
\mathbb{K}^{\dim V}\ar@{->}[0,3]_{ ...
...\ar@{.>}[
-2,0]^{ I_{ C}\o I_{ B}^{-1}} & & &\mathbb{K}^{\dim V'} \\
} $\egroup](img2755.png)
Die obige Transformationsformel erhalten wir auch kürzer aus (10.23), denn danach ist
Betrachten wir nun die Abbildung
![]() welche die
welche die
![]() auf
auf
![]() abbildet.
Bezüglich der Basis
abbildet.
Bezüglich der Basis
![]() auf Ziel- und Start-Raum sieht deren
Matrixdarstellung wie folgt aus:
auf Ziel- und Start-Raum sieht deren
Matrixdarstellung wie folgt aus:
10.28a Beispiel zweier Matrixdarstellungen.
Sei
![]() die Drehung um einen Winkel
die Drehung um einen Winkel
![]() in der Ebene
in der Ebene
![]() um den Nullpunkt. Dies ist noch nicht
wohldefiniert, da die Drehrichtung davon abhängt von welcher Seite aus
man die Ebene
um den Nullpunkt. Dies ist noch nicht
wohldefiniert, da die Drehrichtung davon abhängt von welcher Seite aus
man die Ebene
![]() betrachtet. Wir wählen die Seite auf welcher der Vektor
betrachtet. Wir wählen die Seite auf welcher der Vektor
![]() liegt.
liegt.
![\includegraphics[scale=0.7]{pic-1048}](img2779.png)
Eine Basis von
![]() errät man leicht, z.b.
errät man leicht, z.b.
![]() mit
mit
![]() und
und
![]() .
Bezüglich dieser Basis ist aber eine Drehung schwer zu beschreiben.
Wir haben dies bislang nur in
.
Bezüglich dieser Basis ist aber eine Drehung schwer zu beschreiben.
Wir haben dies bislang nur in
![]() bzgl. der standard-Basis
bzgl. der standard-Basis
![]() gemacht. Um dies zu übertragen benötigen wir ein Basis
gemacht. Um dies zu übertragen benötigen wir ein Basis
![]() , wobei
, wobei
![]() ein Einheitsvektor ist, also z.B.
ein Einheitsvektor ist, also z.B.
![]() und
und
![]() der um
der um
![]() gedrehte Vektor ist.
Ein Vektor
gedrehte Vektor ist.
Ein Vektor
![]() ist genau dann normal auf
ist genau dann normal auf
![]() , wenn das
innere Produkt (siehe (13.1))
, wenn das
innere Produkt (siehe (13.1))
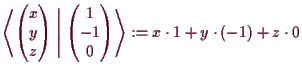
Eine allgemeinere Methode die neue Basis
![]() aus
aus
![]() zu erhalten ist das Gram-Schmidt'sche Orthonormalisierungsverfahren (siehe
(13.9)).
Wie zuvor setzt man
zu erhalten ist das Gram-Schmidt'sche Orthonormalisierungsverfahren (siehe
(13.9)).
Wie zuvor setzt man
![]() , wobei
, wobei
![]() die Länge des
Vektors
die Länge des
Vektors
![]() bezeichnet.
Um nun
bezeichnet.
Um nun
![]() zu erhalten bestimmt man zuerst die Normalprojektion
von
zu erhalten bestimmt man zuerst die Normalprojektion
von
![]() auf
auf
![]() . Diese hat Richtung
. Diese hat Richtung
![]() und als Länge
das innere Produkt
und als Länge
das innere Produkt
![]() und ist somit
durch
und ist somit
durch
![]() gegeben. Der Vektor
gegeben. Der Vektor
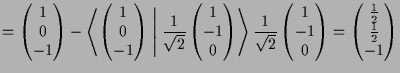 |
![\includegraphics[scale=0.7]{pic-1045}](img2809.png)
Bezüglich dieser Basis sieht also
![]() wie in (10.25) aus, d.h.
wie in (10.25) aus, d.h.
Die Matrixdarstellung von
![]() bezüglich der Basis
bezüglich der Basis
![]() ist somit
ist somit
![\bgroup\color{demo}$\displaystyle [R_\varphi ]_{ C, C}
= \begin{pmatrix}
\cos(\varphi ) & -\sin(\varphi ) \\
\sin(\varphi ) & \cos(\varphi )
\end{pmatrix}$\egroup](img2814.png)
Um die Darstellung bezüglich der ursprünglich gewählten Basis
![]() von
von
![]() zu bestimmen benötigen wir die Matrizen
zu bestimmen benötigen wir die Matrizen
![]() und
und
![]() der Basiswechsel bestimmen, denn es ist
der Basiswechsel bestimmen, denn es ist
Die Matrix
![]() ist durch die Koeffizienten der
ist durch die Koeffizienten der
![]() in der Basis
in der Basis
![]() gegeben, also wegen
gegeben, also wegen
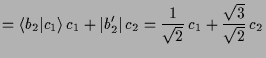 |
![\bgroup\color{demo}$\displaystyle [\operatorname{id}]_{B,C}
=\begin{pmatrix}
\sqrt{2} & \frac1{\sqrt{2}} \\
0 & \frac{\sqrt{3}}{\sqrt{2}}
\end{pmatrix}.
$\egroup](img2822.png)
Die Matrix
![]() erhalten wir entweder auf analoge Weise oder
als Inverse von
erhalten wir entweder auf analoge Weise oder
als Inverse von
![]() , d.h.
, d.h.
![\bgroup\color{demo}$\displaystyle [\operatorname{id}]_{C,B}=[\operatorname{id}]_...
...{2}} & -\frac1{\sqrt{6}} \\
0 & \frac{\sqrt{2}}{\sqrt{3}}
\end{pmatrix}$\egroup](img2823.png)
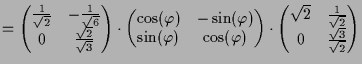 |
||
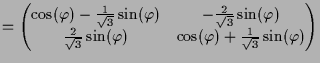 |
Wir können
![]() aber auch allgemeiner auffassen als Abbildung
aber auch allgemeiner auffassen als Abbildung
![]() des Raums, die Punkte um die von
des Raums, die Punkte um die von
![]() erzeugte Achse
um den Winkel
erzeugte Achse
um den Winkel
![]() beschreibt.
Indem wir
beschreibt.
Indem wir
![]() normieren um
normieren um
![]() zu bilden,
erhalten wir eine Basis
zu bilden,
erhalten wir eine Basis
![]() bestehend aus den 3 gleich langen und aufeinander
paarweise orthogonal stehenden Vektoren
bestehend aus den 3 gleich langen und aufeinander
paarweise orthogonal stehenden Vektoren
![]() ,
,
![]() und
und
![]() .
Die Matrixdarstellung von
.
Die Matrixdarstellung von
![]() bezüglich dieser Basis
sieht dann natürlich wie folgt aus, denn die 3.te Koordinate die den
Normalabstand zur Ebene
bezüglich dieser Basis
sieht dann natürlich wie folgt aus, denn die 3.te Koordinate die den
Normalabstand zur Ebene
![]() beschreibt wird bei der Drehung nicht geändert:
beschreibt wird bei der Drehung nicht geändert:
![\bgroup\color{demo}$\displaystyle [R_\varphi ]_{C,C}
=\begin{pmatrix}
\cos\varph...
...varphi & 0 \\
\sin\varphi & \cos\varphi & 0 \\
0 & 0 & 1
\end{pmatrix}$\egroup](img2833.png)
![\bgroup\color{demo}$\displaystyle [I]=(c_1,c_2,c_3) =
\begin{pmatrix}
\frac1{\s...
...3}} \\
0 & -\frac{\sqrt{2}}{\sqrt{3}} & \frac1{\sqrt{3}}
\end{pmatrix}$\egroup](img2835.png)
![\bgroup\color{demo}$\displaystyle [I]^{-1}=I^t=
\begin{pmatrix}
\frac1{\sqrt{2}}...
...\
\frac1{\sqrt{3}} & \frac1{\sqrt{3}} & \frac1{\sqrt{3}}
\end{pmatrix}$\egroup](img2837.png)
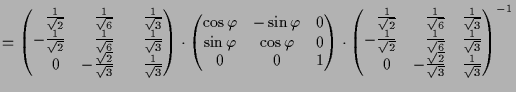 |
||
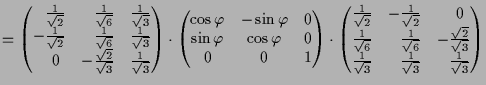 |
||
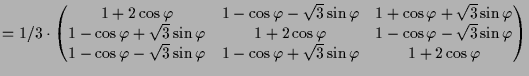 |
Eine andere lineare Abbildung ist die Normalprojektion
![]() auf die Ebene
auf die Ebene
![]() .
Bezüglich der Basis
.
Bezüglich der Basis
![]() ist ihre Matrizendarstellung
offensichtlich durch
ist ihre Matrizendarstellung
offensichtlich durch
![\bgroup\color{demo}$\displaystyle [P]_{C,C} =
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{pmatrix}$\egroup](img2845.png)
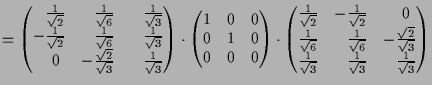 |
||
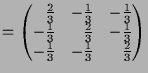 |
Eine weitere lineare Abbildung ist Spiegelung
![]() an der Ebene
an der Ebene
![]() .
Bezüglich der Basis
.
Bezüglich der Basis
![]() ist ihre Matrizendarstellung
offensichtlich durch
ist ihre Matrizendarstellung
offensichtlich durch
![\bgroup\color{demo}$\displaystyle [S]_{C,C} =
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{pmatrix}$\egroup](img2850.png)
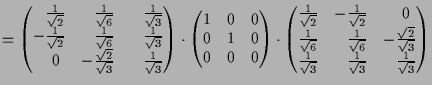 |
||
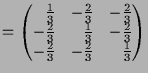 |
Andreas Kriegl 2002-02-01