VO 250082 Dynamical systems and nonlinear differential equations
Email
H. Bruin
for further information for this course.
Announcements
First class on March 5
March 12 is canceled due to Rector's Day.
Easter Break is from March 26 to April 6.
Whit Monday is on May 21.
Schedule
| Day | Time | Room | | from | until |
|---|
| Monday | 9:45--11:15 | HS02 | Lecture | 05.3.2018 | 25.06.2018 |
| Wednesday | 13:15-14:00 | HS02 | Lecture | 7.3.2018 | 27.06.2018 |
| Wednesday | 14:15-15:00 | HS02
Proseminar
Henna Koivusalo | 7.3.2018 | 27.06.2018 |
Exercise Schedule
The proseminar will be every other Wednesday (so one hour proseminar and one hour lecture are swapped).
The exercises are taken from here
and regularly updated.
| Day | Exercises |
|---|
| March 21 | 1-5 |
| April 18 | 6-10 |
| May 2 | 9,10,12,13,11 |
| May 16 | 22,16,17,18 |
| May 30 | 23,20,21,25 |
| June 6 | 26,27,28 |
| June 20 | 29,32,31 |
Contents of the course
Basic notions for continuous and discrete dynamical systems; flows, attractors, and chaos; stability of
stationary points by linearization and by Lyapunov functions, Poincaré-Bendixson theory, bifurcations.
The course will be given in English
Contents of the course (S = Schmeiser's notes, T =
Teschl's book),
St = Strogatz lecture on youtube.
- Bifurcations (S§5. T§6.5. T§11.1.)
- Chaos (T§10.3)
- Cusp bifurcation (S§5.4, St)
- Existence, uniqueness, continuity of solutions of ODEs (S§1. T§2.2. T§2.4.)
- Euler-Lagrange equations (T§8.3. S§10)
- Feigenbaum (bifurcation diagram) (S§6. T§11.1, St)
- Hamiltonian systems (S§10. T§8.3. St)
- Harmonic and other oscillators (S§8.3.)
- Homoclinic orbits and tangles (S Def 10. T§13.2)
- Hopf bifurcation (S§8.4. T p219-220)
- Inhomogeneous linear ODEs (S§2.1. T§3.2.)
- (In)stability of equilibria, sink, sources, saddles, centers (T§3.2.)
- (In)stability of fixed points (T§6.5, T§10.2.)
- Iteration of maps, cobweb diagrams (T§10.2.)
- Kepler problem = two-body problem (T§8.5. S§10)
- Lagrangian = Lagrange function (T§8.3. S§10)
- Legendre transform (T§8.3. S§10)
- Limit cycles (S§8), see also Van der Pol equation and Poincaré-Bendixson.
- Linear ODEs (S§2. T§3.2. T§3.3 St)
- Linearization, the Hartman-Grobman theorem (S Thm 8. T§9.3.)
- Logistic differential equation (T§10.1.)
- Logistic (= quadratic) map (T§10.1. St)
- Lorenz system (S§9. T§8.2., St and
St)
- Lyapunov functions (S§7. T§6.6. St))
- Orbits, omega-limit sets (T§6.3 T§8.1. S Def 4.)
- Pendulum (T§6.7. S§10 (Example 8).)
- Phase portraits (T§3.2.)
- Poincaré maps (T§6.4. T§12.2)
- Poincaré-Bendixson Theorem (S§8.5. T§7.3, St)
- Sensitive dependence on initial conditions (T§10.3)
- Sharkovskiy's Theorem (T§11.2)
- Smale's horseshoe (T§13.1.)
- Stable/unstable manifolds (S Thm 7. T§9.2. T§12.3.)
- Structural stability
- Symbolic dynamics (T§11.5.)
- Strange attractors (T§11.6.)
- Van der Pol equations (S§8, T§7.2, St)
References/Background Reading
- Kathy Alligood, Tim Sauer and James Yorke, Chaos, an Introduction to Dynamical Systems, Springer 1996
ISBN 0-387-94677-2
- Michael Brin and Garrett Stuck, Introduction to Dynamical Systems, Cambridge University Press 2002
ISBN 0-521-80841-3
- Robert Devaney, An Introduction to Cahotic Dynamical Systems, Benjamin and Cummings Publishing 1986,
ISBN 0-8053-1601-9
-
Clark Robinson, Dynamical Systems (Stability, Symbolic Dynamics, and Chaos), CRC Press 1995
ISBN 0-8493-8493-1.
- Steven Strogatz, Nonlinear dynamics and chaos, with applications to physics, biology and
engineering, CRC Press, 2015, ISBN-13: 978-0813349107 or ISBN-10: 0813349109
-
ODE Classnotes
(or in fact book) of Prof. G. Teschl.
Assessment
Will be based on an oral exam (in English by default, aber auf Deutsch ist auch möglich).
Exam Material:
- Linear ODEs and phase portraits
- Existence, uniqueness and continuity of solutions of ODEs
- Iteration of maps on the line (cobweb diagrams), circle and plane
- Types of orbits (fixpoint/equilibria, periodic, saddle/sink/source/center) and their stability
(hyperbolicity)
- Stable and unstable manifold and spaces - Hartman-Grobman Theorem
- Bifurcations (saddle-node/font, transcritical, pitchfork, period doubling, Hopf, cusp)
- Poincaré-Bendixson Theorem, alpha/omega-limit sets and limit cycles
- Lyapunov functions
- Definitions of chaos, sensitive dependence on initial conditions.
- Symbolic dynamics
- Smale's horseshoe
- Hamiltonian systems and first integrals
- Examples: logistic maps, logistic differential equations, Van der Pol equations,
Lorenz equations, harmonic oscillator and pendulum
Course material (Hand-outs)
-
Class notes in pdf (written by Christian Schmeiser)
-
Exercises for the Proseminar.
-
An Applet for cobweb diagrams for the logistic family.
-
An Applet for the bifurcation diagram for the logistic family.
- Hand-out about structural stability
- Hand-out about symbolic itineraries
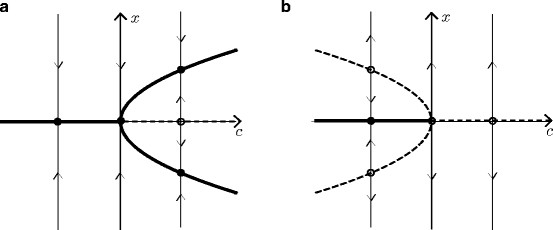
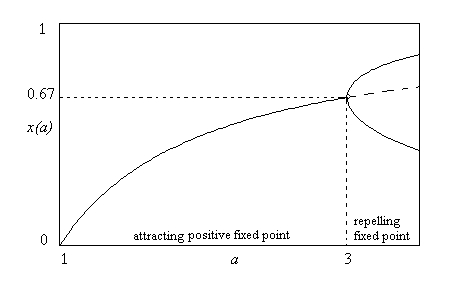
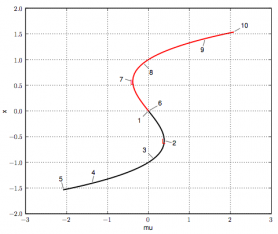
- Some bifurcation diagrams:
 |
 |
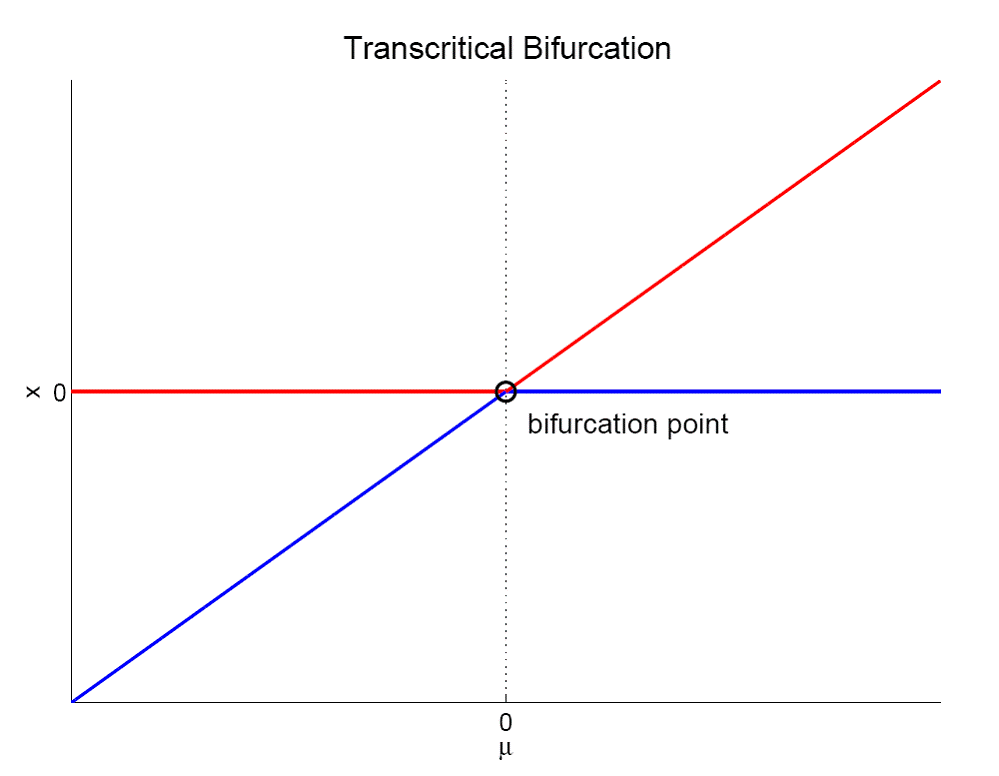 |
| Pitchfork bifurcation | Period doubling bifurcation | Transcritical bifurcation |
|---|
 |
 |
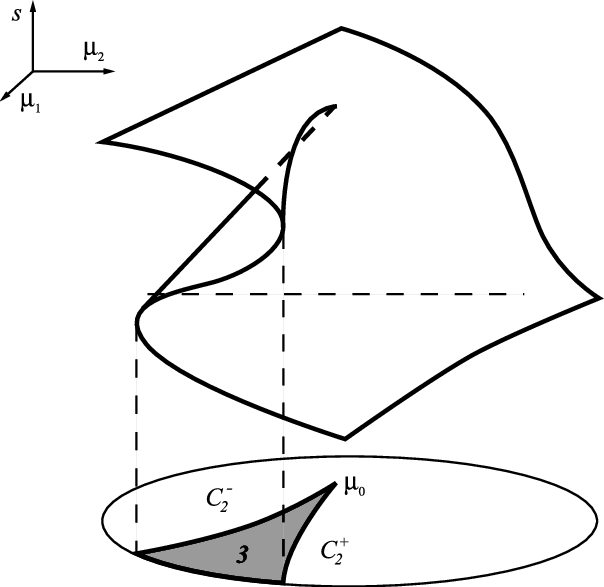 |
| Spruce budworm (Caterpillar and Moth) | Two saddle node (= fold) bifurcations meeting in a cusp (x,k)-plane |
Bifurcation surface for cusp (projecting to (r,k)-plane |
as well as a lecture by
Strogatz on the same topic.
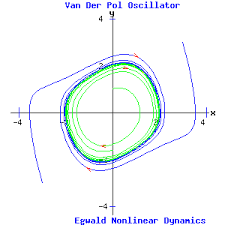
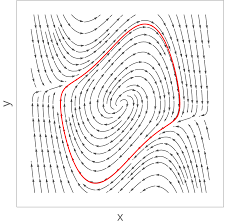
- Some phase portraits for the Van der Pol oscillator:
and also some youtube videos here,
here,
and a lecture by
Strogatz (Cornell University).
-
Some youtube videos on Huygens resonance
here,
here,
here, and
here, and if you still didn't have enough, also here.
-
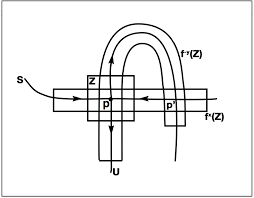
Some youtube videos on Smale and his horseshoe:
here and
here.
 |
 |
 |
| Smale's horseshoe | A homoclinic tangle | Another homoclinic tangle |
-
Some youtube videos on Lorenz and the Lorenz attractor.
here,
here, and
here
and the Wikipedia page
- Written out class notes of June 18 in
pdf.
-
Some youtube videos on three-body choreographies,
here,
here, and
here
and here.
Or this one.
-
Some youtube videos on the Kepler problem (motion by the Earth and Sun), on
gravitation,
by Feynman (sort of),
and general.
-
Online Lecture by Anima Nagar
-
Updated April 2018