Next: 18.4 Gewöhnliche Differentialgleichungen Up: 18 Integralrechnung Previous: 18.2 Unbestimmte Integrale
18.3.1 Definition. Uneigentliche Integrale.
Wir wollen nun auch Integrale
![]() behandeln, bei denen
entweder der Integrand
behandeln, bei denen
entweder der Integrand
![]() oder der Integrationsbereich
oder der Integrationsbereich
![]() unbeschränkt ist.
In diesen Fall spricht man von uneigentlichen Integralen und definiert z.B. falls
unbeschränkt ist.
In diesen Fall spricht man von uneigentlichen Integralen und definiert z.B. falls
![]() bei
bei
![]() unbeschränkt aber auf jeden Teilintervall
unbeschränkt aber auf jeden Teilintervall
![]() von
von
![]() mit
mit
![]() Riemann-integrierbar ist:
Riemann-integrierbar ist:
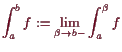
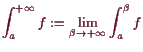
18.3.2 Beispiele uneigentlicher Integrale.
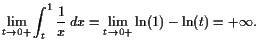
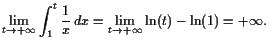

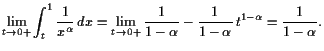
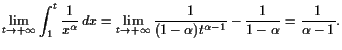

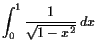 |
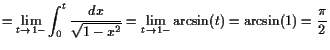 |
|
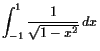 |
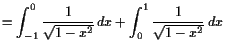 |
|
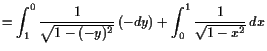 |
||
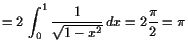 |
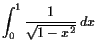 |
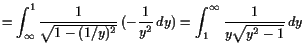 |
|
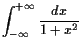 |
||

18.3.3 Lemma. Cauchy-Kriterium für uneigentliche
Integrale.
Es existiere
![]() für alle
für alle
![]() .
Dann existiert das uneigentliche Integral
.
Dann existiert das uneigentliche Integral
![]() genau dann wenn
genau dann wenn
![]() für
für
![]() .
.
18.3.4 Proposition. Integralkriterium für
Reihenkonvergenz.
Es sei
![]() uneigentlich Riemann-integrierbar
und
uneigentlich Riemann-integrierbar
und
![]() für
für
![]() .
Dann konvergiert
.
Dann konvergiert
![]() absolut.
absolut.

Beweis. Es ist
Beispiel.
Wir haben in (18.3.2) gesehen, daß das uneigentliche Integral
![]() für
für
![]() existiert. Also
ist
existiert. Also
ist
![]() für diese
für diese
![]() konvergent.
konvergent.
18.3.5 Definition. Euler'sche Gammafunktion.
Uner der Euler'sche Gammafunktion versteht man die Funktion
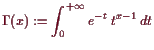 für
für

18.3.6 Lemma. Gammafunktion als Fortsetzung von
Faktorielle.
Es gilt folgende Rekursionsformel für die Euler'sche Gamma-Funktion:
Beweis. Es ist
18.3.8 Bemerkung.
Man kann zeigen, daß
![]() für
für
![]() (siehe [Heuser, Analysis 2, Seite 198]).
Insbesonders ist
(siehe [Heuser, Analysis 2, Seite 198]).
Insbesonders ist
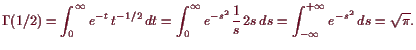
18.3.7 Bemerkung. Integration von Kurven im
Mehrdimensionalen.
Der Hauptsatz (18.2.2) läßt sich wie folgt auf's mehrdimensionale übertragen.
Wenn
![]() ist, dann verstehen wir unter dem
Riemann-Integral
ist, dann verstehen wir unter dem
Riemann-Integral
![]() den Vektor
den Vektor
Ist nun
![]()
![]() und die Strecke
und die Strecke
![]() ,
dann ist
,
dann ist
![]()
![]() als Zusammensetzung mit der
affinen Funktion
als Zusammensetzung mit der
affinen Funktion
![]() und hat Ableitung
und hat Ableitung
![]() .
Nach dem Hauptsatz angewendet auf die Kurve
.
Nach dem Hauptsatz angewendet auf die Kurve
![]() ist somit
ist somit
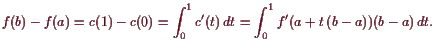
Andreas Kriegl 2002-07-01