Next: 18.3 Uneigentliche Integrale Up: 18 Integralrechnung Previous: 18.1 Riemann-Integral
18.2.1 Definition. Unbestimmte Integral.
Es sei
![]() Riemann-integrierbar und
Riemann-integrierbar und
![]() . Nach dem Lebesgue'schen
Integrabilitätskriterium (18.1.4) existiert dann für jedes
. Nach dem Lebesgue'schen
Integrabilitätskriterium (18.1.4) existiert dann für jedes
![]() auch
auch
![]() .
Diese Abbildung
.
Diese Abbildung
![]() heißt (ein) unbestimmtes Integral von
heißt (ein) unbestimmtes Integral von
![]() .
.
18.2.2 Hauptsatz der Differential und
Integralrechnung.
Das unbestimmte Integral
![]() jeder Riemann-integrierbaren Funktion
jeder Riemann-integrierbaren Funktion
![]() ist stetig.
ist stetig.
Ist der Integrand
![]() stetig bei
stetig bei
![]() , so ist
, so ist
![]() differenzierbar bei
differenzierbar bei
![]() mit
Ableitung
mit
Ableitung
![]() .
.
Umgekehrt sei
![]() stetig differenzierbar mit Ableitung
stetig differenzierbar mit Ableitung
![]() . Dann ist
. Dann ist
![]() Riemann-integrierbar und
Riemann-integrierbar und
![]() .
.
Jede Funktion
Beweis. Es ist
Ist
![]() zusätzlich stetig bei
zusätzlich stetig bei
![]() , so existiert zu
, so existiert zu
![]() ein
ein
![]() s.d.
s.d.
![]() für alle
für alle
![]() mit
mit
![]() und damit ist
und damit ist
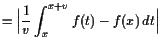 |
||
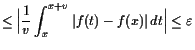 |
Ist
![]() also stetig, so ist
also stetig, so ist
![]() eine Stammfunktion von
eine Stammfunktion von
![]() .
.
Sei nun
![]() stetig differenzierbar mit Ableitung
stetig differenzierbar mit Ableitung
![]() .
Somit ist
.
Somit ist
![]() eine Stammfunktion von
eine Stammfunktion von
![]() und nach dem 1. Teil
ist das unbestimmte Integral
und nach dem 1. Teil
ist das unbestimmte Integral
![]() ebenfalls eine Stammfunktion,
also ist die Ableitung von
ebenfalls eine Stammfunktion,
also ist die Ableitung von
![]() gleich 0 und damit nach dem Spezialfall des
Mittelwertsatzes
(17.1.4)
gleich 0 und damit nach dem Spezialfall des
Mittelwertsatzes
(17.1.4)
![]() konstant, also
konstant, also
![]() .
[]
.
[]
Bemerkung.
Der Hauptsatz besagt also, daß Integrieren und Differenzieren im wesentlichen,
d.h. bis auf Addition einer Konstanten, invers zueinander sind.
Genauer: Es ist Differenzieren
![]() auf der Menge der
differenzierbaren Funktionen
auf der Menge der
differenzierbaren Funktionen
![]() nicht injektiv, denn
nicht injektiv, denn
![]()
![]()
![]() ist konstant.
ist konstant.
Jedoch ist Differenzieren
![]() auf der Menge
auf der Menge
![]() der stetig
differenzierbaren Funktionen
der stetig
differenzierbaren Funktionen
![]() surjektiv als Abbildung in die Menge
surjektiv als Abbildung in die Menge
![]() der stetigen Abbildungen
der stetigen Abbildungen
![]() , denn zu jedem
, denn zu jedem
![]() definiert
definiert
![]() eine Stammfunktion.
eine Stammfunktion.
Somit definiert dieses unbestimmte Integral eine rechtsinverse Abbildung
![]() zum Differenzieren
zum Differenzieren
![]() , für
die weiters gilt:
, für
die weiters gilt:
![]() ist eine konstante Abbildung.
ist eine konstante Abbildung.
Wenn wir
![]() auf den Teilvektorraum
auf den Teilvektorraum
![]() einschränkten, dann sind Differenzieren
einschränkten, dann sind Differenzieren
|
und (unbestimmt) Integrieren
| ||
18.2.3 Beispiele von Stammfunktionen.
Wir können Formeln die wir für das Differenzieren erhalten haben
als Formeln für (unbestimmte) Integrale interpretieren:
| oder auch |
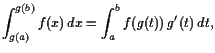
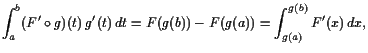
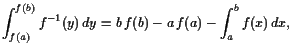
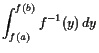 |
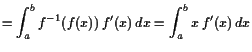 |
|
![$\displaystyle = \left[x f(x)\right]_{x=a}^b - \int_a^b 1 f(x) dx$](img1809.gif) |
||
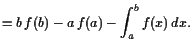 |

18.2.4 Definition. Logarithmus.
Wir können nun eine direkte exakte Definition des Logarithmus geben (vgl. mit
(17.3.5.3)):
Es sei der natürliche Logarithmus definiert durch
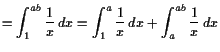 |
||
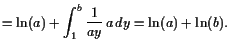 |
Nach den Sätzen (16.4.4) und (17.3.4)
über inverse Funktionen existiert somit die differenzierbare
Umkehrfunktion
![]() (die Exponentialfunktion)
mit
(die Exponentialfunktion)
mit
![]() (vgl. mit (17.3.5.3))
Weiters folgt aus den Aussagen für
(vgl. mit (17.3.5.3))
Weiters folgt aus den Aussagen für
![]() , daß
, daß
![]() und
und
![]() .
Es ist
.
Es ist
18.2.5 Definition. Allgemeine Potenz und Logarithums.
Sei nun
![]() . Dann setzen wir
. Dann setzen wir

Und für
![]() heißt die Umkehrfunktion zu
heißt die Umkehrfunktion zu
![]() der Logarithmus
der Logarithmus
![]() zur Basis
zur Basis
![]() .
Diese Definition von
.
Diese Definition von
![]() stimmt für
stimmt für
![]() mit der in
Mathematik 1 gegebenen Definition
mit der in
Mathematik 1 gegebenen Definition
![]() überein, denn
überein, denn
18.2.6 Definition. Hyperbolische Winkelfunktionen.
Es sei
![]() eine Funktion. Dann ist
eine Funktion. Dann ist
![]() eine gerade und
eine gerade und
![]() eine ungerade
Funktion mit
eine ungerade
Funktion mit
![]() .
.
Wenden wir dies insbesonders auf die Funktione
![]() an, so erhalten wir
den Sinushyperbolicus
an, so erhalten wir
den Sinushyperbolicus
![]() ,
und den Cosinushyperbolicus
,
und den Cosinushyperbolicus
![]() . In Analogie zu den üblichen Winkelfunktionen
definieren wir den Tangenshyperbolicus als
. In Analogie zu den üblichen Winkelfunktionen
definieren wir den Tangenshyperbolicus als
![]() .
.

Man kann leicht folgende Aussagen beweisen:

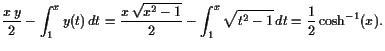 |
18.2.7 Bemerkung. Integration rationaler Funktionen.
Folgende rationale Ausdrücke können wir integrieren:
Sei nun
![]() eine Nullstelle von
eine Nullstelle von
![]() .
Dann können wir
.
Dann können wir
![]() durch
durch
![]() so oft wie möglich dividieren
und erhalten
so oft wie möglich dividieren
und erhalten
![]() für eine natürliche Zahl
für eine natürliche Zahl
![]() und ein Polynom
und ein Polynom
![]() mit
mit
![]() .
Somit ist
.
Somit ist
![]() .
Folglich betrachten wir
.
Folglich betrachten wir
18.2.8 Proposition. Partialbruchzerlegung im
Komplexen.
Es seien
![]() und
und
![]() Polynome mit komplexen Koeffizienten und mit
Polynome mit komplexen Koeffizienten und mit
![]() .
Weiters seien
.
Weiters seien
![]() die verschiedenen Nullstellen von
die verschiedenen Nullstellen von
![]() und
und
![]() ihre Vielfachheit.
Dann ist
ihre Vielfachheit.
Dann ist
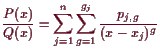
Wir können nun die Partialbruchzerlegung verwenden um rationale Funktionen zu integrieren.
18.2.9 Beispiel des Integrals einer rationalen Funktion.
Es sei die rationale Funktion
![]() gegeben.
Division mit Rest liefert:
gegeben.
Division mit Rest liefert:
18.2.10 Proposition. Partialbruchzerlegung im
Reellen.
Es seien
![]() und
und
![]() Polynome mit reellen Koeffizienten und mit
Polynome mit reellen Koeffizienten und mit
![]() .
Weiters seien
.
Weiters seien
![]() die verschiedenen reellen Nullstellen von
die verschiedenen reellen Nullstellen von
![]() und
und
![]() ihre Vielfachheit.
Seien schließlich
ihre Vielfachheit.
Seien schließlich
![]() die echt komplexen
verschiedenen Nullstellen von
die echt komplexen
verschiedenen Nullstellen von
![]() und
und
![]() ihre Vielfachheit.
Dann ist
ihre Vielfachheit.
Dann ist
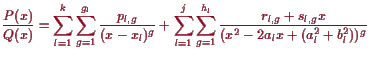
Beweis. Für jede komplexe Nullstelle
Somit ist
![]() und
wegen (18.2.8)
und
wegen (18.2.8)
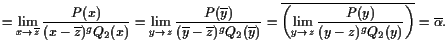 |
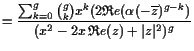 |
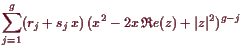
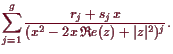
Beachte, daß eine Stammfunktion von
![]() wie
folgt mittels Substitutionen
wie
folgt mittels Substitutionen
![]() und
und
![]() bestimmt werden kann:
bestimmt werden kann:
Andreas Kriegl 2002-07-01